
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Що таке мультиколеніарність та як її визначати?Содержание книги
Поиск на нашем сайте
Мультиколінеарність – це наявність таких значень r, при яких │ rxy│<│ rxx│, тобто коефіцієнт парної кореляції між факторами xj більший за модулем, ніж коефіцієнт кореляції між відповідними х та показниками у. Наявність мультиколеніарності перешкоджає встановленню дійсного впливу кожного фактора на прогнозований показник. В такому випадку система нормальних рівнянь стає виродженою і отримані результати не можна вважати надійними. Для визначення мультиколеніарності розраховується система парних коефіцієнтів кореляції, які відображають тісноту зв'язку пар факторів, що входять в модель. В практичних цілях рекомендується вважати зв'язок мульти-коленіарним, якщо коефіцієнт парної кореляції між двома факторами по абсолютній величині дорівнює або більше 0,8. Оскільки вказана межа значення коефіцієнта парної кореляції визначена довільно і нічим не обґрунтована, існують спроби певним чином обґрунтувати межі мультиколеніарності. 63. Що таке стійкість розв’язку при визначенні коефіцієнтів рівняння множинної регресії. Реалізація у регресійному аналізі чисельних методів розв”язку, зокрема методу найменших квадратів, передбачає визначення стійкості розв”язку. Поняття стійкості розв”язку в свою чергу визначається обумовленістю системи лінійних рівнянь, яка у векторно-матричній формі запису може бути представлена такою формулою
де: А – вектор-стовпець коефіцієнтів Аналітичний розв”язок цієї системи має вигляд
Таким чином, якщо незначні зміни у правій частині системи ведуть до суттєвої зміни розв”язку А, то така система називається погано обумовленою, а сам розв”язок – нестійким. В результаті, не дивлячись на те, що розв”язок отриманий, регресійна модель буде суперечити суті економічного, фізичного, технологічного чи іншого явища. Вимога адекватності порушується і застосовувати отримане рівняння регресії не можна. В цьому плані ми як би знаходимо математичне підтвердження того факту, що підбір факторів впливу для кореляційно-регресійної залежності в першу чергу має здійснюватися на основі попереднього аналізу і дотримання економічної, фізичної, технологічної і т.п. суті (логіки) зв”язків у системі дослідження (тобто, структури системи).
Щодо кількісних оцінок обумовленості системи рівнянь, то в навчальній та науковій літературі можна знайти такі рекомендації. Рекомендують, наприклад, розраховувати числа обумовленості матриці
Числа обумовленості розраховують як добуток норм прямої та оберненої матриць до вказаної матриці системи рівнянь. Ці числа означають, у скільки разів може збільшитися відносна похибка в коефіцієнтах А за наявності похибки у вихідній матриці М. Для розрахунку чисел обумовленості матриці М у програмному середовищі Mathcad існують вмонтовані функції cond1(M), cond2(M), conde(M), condi(M) (від англ. сondition – умова, обумовленість). Різняться числа обумовленості несуттєво, тим більше, що за критерій обумовленості береться не саме число, а його порядок. Зустрічаються такі рекомендації: при значеннях cond, що має порядок 101 розв”язок можна вважати стійким; якщо число обумовленості сягає порядку 102..103, то розв”язок системи суперечливий; при значеннях cond порядку 104 і вище система рівнянь погано обумовлена. В останньому випадку ми матимемо значну закорельованість факторів та статистичних характеристик, тому таблиця мультиколінеарності (коефіцієнтів парної кореляції між факторами) рекомендується як ще один побічний критерій, за яким можна визначити стійкість розв”язку. Бажано, щоб максимальний коефіцієнт парної кореляції між факторами не перевищував значення 0.4, але практично витримати цю умову вдається не завжди. Якщо коефіцієнти парної кореляції між факторами приймають значення 0.8 і вище, то вірогідний висновок про наявність мультиколінеарності (недопустимої закорельованості факторів). Існує також обмеження, за яким коефіцієнти парної кореляції між факторами та показником у за модулем повинні бути суттєво більшими від значення за модулем відповідних коефіцієнтів парної кореляції між самими факторами. Необхідною умовою існування добре обумовленої матриці М є відмінність від нуля визначника цієї матриці. У випадку det M ≈ 0 матриця М є погано обумовленою, містить майже лінійно залежні вектори-стовпці, а тому її розв”язок буде нестійким. Зустрічається також рекомендація, щоб det M приймав значення, більші порівняно з коефіцієнтами матриці М.
Чим менш стійкий розв”язок вихідної матриці системи рівнянь, тим вужчий діапазон значень довірчих інтервалів для коефіцієнтів рівняння регресії. Довірчі інтервали визначають із застосуванням t -критеріїв Стьюдента на рівні значущості α (α = 0.05) та при ступенях вільності n – N
де
У формулі (3.2.13)
а із курсу вищої математики пригадуємо, що алгебраїчні доповнення визначаються як мінор матриці М, помножений на (-1)i+k, де i – кількість рядків мінора, k – кількість стовпців мінора. Оскільки у кореляційно-регресійному аналізі мають справу з квадратними матрицями М, то даний множник приймає значення 1 і його можна опускати. Під мінором матриці М розуміють визначник матриці на порядок меншої за М, яку можна отримати, “викреслюючи” (умовно) і -тий рядок та k -ий стовпець у матриці М, які на перехресті визначають один з діагональних елементів. 64. Як оцінюють адекватність рівняння множинної регресії Під адекватністю регресійної моделі розуміють відповідність моделі досліджуваному процесу. Кількісна перевірка адекватності моделі зводиться до перевірки отриманого рівняння регресії за критерієм Фішера
де:
65. Як розраховують істотність, суттєвість рівняння множинної регресії? Під істотністю, або інформативністю чи значущістю, багатофакторної регресійної моделі розуміють як кількість, так і якість факторів, які б найбільш повно описували зміну досліджуваного показника та уможливлювали прийняття ефективних управлінських рішень. Кількісною мірою істотності моделі виступає коефіцієнт детермінації D, який визначається як квадрат коефіцієнта множинної кореляції R. Коефіцієнт детермінації, помножений на 100%, визначає, на скільки відсотків зміна показника у обумовлена зміною включених у рівняння факторів х1…N. Коефіцієнт множинної кореляції розраховується (якщо множинна регресія визначалася у відхиленнях від середніх значень) за формулою
де v – сума квадратів відхилень від середніх значень,
Бажано, щоб розрахований коефіцієнт множинної кореляції приймав значення, більші за 0.95-0.96. Стандартна статистична перевірка коефіцієнта множинної кореляції виконується за F -критерієм Фішера, розрахункове значення якого має задовольняти умові
де З вищенаведеного напрошується висновок, що в модель необхідно включати таку кількість факторів, за якою можна було б отримати D → 1 (або, відповідно, R → 1). 66. Якщо в рівнянні множинної регресії присутні 3 і більше факторів, який метод вибору з цих факторів для включення в дане рівняння застосовують? У випадку багатофакторного (j= 1,2,3, …, N)регресійного аналізу побудова моделей зводиться до визначення лінійної залежності виду де коефіцієнти 67.(Визначення моделей з ризику.68. Поняття якими оперують в моделях ризику та не визначеності.). Разом. Прийняття рішень – аналітичний підхід для вибору альтернативи або напряму дії. У теорії прийняття рішень існують три типи моделей прийняття рішень: Ø прийняття рішень в умовах визначеності – той, хто приймає рішення, на певне знає наслідки дії або обраного рішення; Ø прийняття рішень в умовах ризику – той, хто приймає рішення, знає ймовірність появи результату або наслідки кожної дії прийняття рішень в умовах невизначеності – тому, хто приймаєрішення, не відома ймовірність появи результату Приймати рішення набагато ефективніше не в умовах ризику, а в умовах визначеності.
У прийнятті рішень в умовах визначеності той, хто приймає рішення, знає наслідки своїх дій і вибере альтернативу, яка дасть змогу отримати найкращий результат. Зазначимо, що ситуація, яка розглядається, передбачає прийняття рішення саме в умовах ризику. Той, хто приймає рішення, робитиме спробу максимізувати очікуваний результат. Тут, як і в більшості випадків, йдеться про грошовий результат. При цьому менеджери, які приймають рішення, розглядають усі альтернативи та стани природи. Що розуміють під цими термінами? Альтернатива – напрям дії або стратегія, яку може обрати той, хто приймає рішення (наприклад, замовляти маркетингові дослідження). Стан природи – ситуація, на яку той, хто приймає рішення, не може вплинути або може вплинути дуже слабо (кон’юктура ринку). Для зображення альтернатив рішень менеджера використовують дерево рішень. Для цього застосуємо такі позначки: o - це вузол рішення, з якого можна обрати одну або кілька альтернатив. ¡ - це вузол стану природи, з кого може з’явитись один стан природи. Аби допомогти компанії визначити її рішення, можна також побудувати таблицю рішень (платіжну таблицю, платіжну матрицю). Для кожної альтернативи (дії) та певного стану природи є післядія (або наслідок), яка зазвичай подається у грошовому вираженні і називається умовним значенням (умовний прибуток). При цьому всі альтернативи записуються в лівій частині таблиці, умовні стани природи – у верхній частині таблиці, а умовні значення – розміщуються посередині таблиці. Що краще використовувати – таблиці рішень чи дерева рішень? Якщо є один вибір рішень і один стан природи, зручніше використовувати таблицю рішень. Якщо існують два або більше послідовних рішень, причому подальші рішення базуються на наслідках попередніх, використання дерев цілей є потужнішим інструментом порівняно з таблицею рішень. Дерево цілей – це графічне зображення процесу, яке визначає альтернативи рішень, стану природи та їхні відповідні ймовірності віддачі для кожної комбінації альтернатив і стану природи. За критерій рішення для аналізу дерева цілей найчастіше обирають очікувану грошову віддачу (expected monetary value, EMV) для кожного варіанта. Це число представляє очікувану цінність варіанта, тобто таку віддачу, яку ми отримаємо, якщо зможемо повторити рішення більшу кількість разів. Найпопулярнішим рішенням є вибір варіанта, який має максимальне значення EMV. EMV для варіанта – це сума можливих надходжень (віддач) варіанта, кожна зважена на імовірність появи віддачі:
Аналіз проблеми з використанням дерева цілей включає в себе п’ять кроків (рис.3.6.1). КРОК 5 Вирішити проблему підраховуючи очікувану віддачу, в грошовому вираженні EMV для кожного вузла, стану природи КРОК 4 Оцінити віддачу для кожної можливої комбінації альтернатив і станів природи КРОК 3 Визначити ймовірності стану природи КРОК 2 Структурувати або намалювати дерево цілей КРОК 1 Визначити проблему Рис.3.6.1- Методика аналізу проблеми з використанням дерева цілей
Для оцінки очікуваної віддачі (або інший термін – післядії, а це може бути, наприклад, прибуток/збиток) використовується процедура, що має назву “зворотна індукція“. На вилці дій вибирається та гілка, яка має найбільше значення для очікуваної віддачі. Правостороння вилка дій (“не купувати” виключається) перекреслюється подвійною лінією. Починаючи праворуч від дерева, рухаємося над вузлами рішень. Очікуваною цінністю досконалої інформації (Expected Value Perfect Information) називається різниця між очікуваною віддачею (від рішення) в умовах визначеності та в умовах ризику:

Щоб визначити очікувану цінність в умовах визначеності, обираємо найкращу альтернативу для кожного стану природи і викликану нею віддачу перемножуємо на ймовірність появи цього стану природи:
|
||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 439; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.137.193 (0.009 с.) |

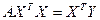 , (3.2.9)
, (3.2.9)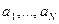 рівняння регресії, тобто шуканих значень розв”язку (попутно зауважимо, що коефіцієнт
рівняння регресії, тобто шуканих значень розв”язку (попутно зауважимо, що коефіцієнт  розраховується за окремо складеним рівнянням); Х, Y - відповідно матриця та вектор-стовпець відхилень значень вхідних даних xj,i та уі від їх середніх величин (для факторів впливу хj,i беруться середні величини
розраховується за окремо складеним рівнянням); Х, Y - відповідно матриця та вектор-стовпець відхилень значень вхідних даних xj,i та уі від їх середніх величин (для факторів впливу хj,i беруться середні величини 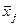 по кожному з факторів j з масиву вхідних даних); Т – знак транспонування матриці.
по кожному з факторів j з масиву вхідних даних); Т – знак транспонування матриці. . (3.2.10)
. (3.2.10) . (3.2.11)
. (3.2.11)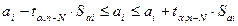 , (3.2.12)
, (3.2.12) - стандартне відхилення коефіцієнта регресії,
- стандартне відхилення коефіцієнта регресії, . (3.2.13)
. (3.2.13)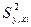 - залишкова дисперсія,
- залишкова дисперсія,  - алгебраїчні доповнення діагональних елементів матриці М. Дисперсію
- алгебраїчні доповнення діагональних елементів матриці М. Дисперсію  , (3.2.14)
, (3.2.14)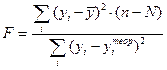 , (3.2.8)
, (3.2.8)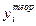 - значення величини показника, знайдене за рівнянням регресії в точках і = 1,2,…, n;
- значення величини показника, знайдене за рівнянням регресії в точках і = 1,2,…, n;  - середня величина значень
- середня величина значень  . Модель вважається адекватною на рівні значущості α, якщо
. Модель вважається адекватною на рівні значущості α, якщо  . Для студентських робіт рішення про адекватність можна також приймати, порівнюючи розраховані за рівнянням значення у в точках і = 1,2,…, n із вхідними даними уі з масиву Y. Якщо розраховані в даних точках значення у співпадатимуть із значеннями уі з прийнятною для дослідника точністю, то робиться висновок про адекватність моделі. Висновок про адекватність отриманої моделі дослідник може також зробити на основі свого бачення практичної цінності виведеного рівняння регресії. У цьому плані можна, наприклад, розглядати прогнозні якості регресійної залежності. При цьому всю вибірку вхідних даних розбивають на дві підвибірки. Одна підвибірка служить як нові вхідні дані для побудови в її межах додаткового рівняння регресії. За іншою – контрольною підвибіркою – здійснюють перевірку отриманого додаткового рівняння, тобто, підставивши значення факторів впливу, розраховують значення у та порівнюють їх із значеннями уі із контрольної підвибірки. Якщо розраховані таким чином “прогнозні” значення співпадатимуть із значеннями з контрольної підвибірки, забезпечивши достатню точність, то можна зробити висновок про адекватність основної моделі та її прийнятність для прогнозування значень досліджуваного показника. Величину підвиборок, тобто їхнє співвідношення в межах основної вибірки вхідних даних, необхідно встановити таким чином, щоб були витримані статистичні критерії.
. Для студентських робіт рішення про адекватність можна також приймати, порівнюючи розраховані за рівнянням значення у в точках і = 1,2,…, n із вхідними даними уі з масиву Y. Якщо розраховані в даних точках значення у співпадатимуть із значеннями уі з прийнятною для дослідника точністю, то робиться висновок про адекватність моделі. Висновок про адекватність отриманої моделі дослідник може також зробити на основі свого бачення практичної цінності виведеного рівняння регресії. У цьому плані можна, наприклад, розглядати прогнозні якості регресійної залежності. При цьому всю вибірку вхідних даних розбивають на дві підвибірки. Одна підвибірка служить як нові вхідні дані для побудови в її межах додаткового рівняння регресії. За іншою – контрольною підвибіркою – здійснюють перевірку отриманого додаткового рівняння, тобто, підставивши значення факторів впливу, розраховують значення у та порівнюють їх із значеннями уі із контрольної підвибірки. Якщо розраховані таким чином “прогнозні” значення співпадатимуть із значеннями з контрольної підвибірки, забезпечивши достатню точність, то можна зробити висновок про адекватність основної моделі та її прийнятність для прогнозування значень досліджуваного показника. Величину підвиборок, тобто їхнє співвідношення в межах основної вибірки вхідних даних, необхідно встановити таким чином, щоб були витримані статистичні критерії.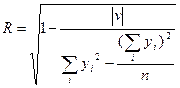 , (3.2.5)
, (3.2.5)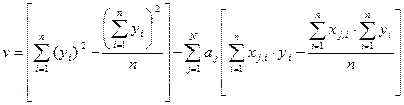 . (3.2.6)
. (3.2.6)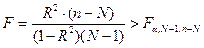 , (3.2.7)
, (3.2.7)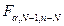 - табличне значення F- розподілу на рівні значущості α та для ступенів вільності N-1, n-N. Найчастіше приймають α = 0.05, а розрахункове значення F повинно відрізнятися від табличного хоча би на порядок.
- табличне значення F- розподілу на рівні значущості α та для ступенів вільності N-1, n-N. Найчастіше приймають α = 0.05, а розрахункове значення F повинно відрізнятися від табличного хоча би на порядок.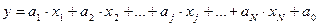 , (3.2.4)
, (3.2.4)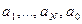 розраховуються за методом найменших квадратів.
розраховуються за методом найменших квадратів.




