
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Суть задачі динамічного програмування.Содержание книги
Поиск на нашем сайте
Суть задачі динамічного програмування полягає у тому,щоб з області можливих станів її вибрати такий,при якому критерій Wбуде оптимальним. Приклад. Нехай треба сформуватирозробкуS нафтогазових родовищ на період
Сумарний дохід за к- етапів буде як функція управління В якості оптимального значення обирають.Переносячи на попередні кроки приходять до оптимального стану систему на початку стані системи.Даний принцип відповідно до якого оптимальне продовження процесу відшуковується відносно процесу досягнутого на даний момент називається принципом оптимальності Велмена. 46. Суть принципу Бемнана. Для прийняття оптимального рішення на k -му кроці багатокрокового процесу потрібна оптимальність рішень на всіх його попередніх кроках, а сукупність усіх рішень дає оптимальний розв’язок задачі лише в тому разі, коли на кожному кроці приймається оптимальне рішення, що залежить від параметра етапу Цей факт є основою методу динамічного програмування і є сутністю так званого принципу оптимальності Р. Белмана, який формулюється так: Оптимальний розв’язок багатокрокової задачі Доведемо справедливість такого твердження, міркуючи від супротивного. Нехай маємо задачу на максимізацію функції Принцип оптимальності еквівалентний твердженню, що вектор
але
що суперечливо. Отже, принцип оптимальності доведено. 47. Суть задачі вибору шляху в динамічній постановці. Нехай відомо схеми деякого переміщення.Рух можливий в будь якому напрямку але з різною вартістю.Необхідно знайти такий шлях з точки для розв'язку задачі розіб’ємо шляхи на 4 вертикальні зони розрахунку.Алгоритм розрахунку починаємо для кінцевої точки Перше знаходимо шляхи від
Вибираючи той який має найменше значення критерія переміщення найменш.є шлях переміщення 19, проставляємо стрілку над шляхом, що визначає переміщення Такий розрахунок застосовуємо послідовно для інших точок,визначаємо множину всіх можливих шляхів переміщень або управлінь V.Результат є таким (стрілочки на малюнку відповідно переміщенню) Те управління яке починається в
|
||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 273; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.105.80 (0.006 с.) |

 при чомувідомо сума грошовихінвестиційD,якірозподіляються за роками ti. Початковий стан системи
при чомувідомо сума грошовихінвестиційD,якірозподіляються за роками ti. Початковий стан системи  який характеризується кількістю грошових коштів вже вкладених в розробку та кінцевий стан системи
який характеризується кількістю грошових коштів вже вкладених в розробку та кінцевий стан системи  ,який характеризується запланованою сумою інвестицій D.Треба таким чином розприділити кошти D за роками
,який характеризується запланованою сумою інвестицій D.Треба таким чином розприділити кошти D за роками  щоб сумарний дохід підприємства був maxW.Позначимо через
щоб сумарний дохід підприємства був maxW.Позначимо через  суму коштів,що виділяються на початок року і-тому родовищу.Нехай кошти на і-тому етапі вже розподілені тобто вибраним управління
суму коштів,що виділяються на початок року і-тому родовищу.Нехай кошти на і-тому етапі вже розподілені тобто вибраним управління  ,яке означає що на початок і-того року родовищу
,яке означає що на початок і-того року родовищу  виділені кошти
виділені кошти  ,кошти на х-етапи розрахунків отримаємо набір управління
,кошти на х-етапи розрахунків отримаємо набір управління
 У динамічному програмуванні для maxW починають планувати процес з х- того року, поступово переходячи до х-1,х-2 і до
У динамічному програмуванні для maxW починають планувати процес з х- того року, поступово переходячи до х-1,х-2 і до  як функцію стану системи на х-1.
як функцію стану системи на х-1. , визначеного на попередньому кроці.
, визначеного на попередньому кроці. має ту властивість, що яким би не був стан системи
має ту властивість, що яким би не був стан системи  в результаті деякої кількості кроків, необхідно вибирати управління
в результаті деякої кількості кроків, необхідно вибирати управління  на найближчому кроці так, щоб воно разом з оптимальним управлінням на всіх наступних кроках приводило до максимального виграшу на всіх останніх кроках, включаючи даний.
на найближчому кроці так, щоб воно разом з оптимальним управлінням на всіх наступних кроках приводило до максимального виграшу на всіх останніх кроках, включаючи даний. і вектор
і вектор  повинен бути оптимальним планом
повинен бути оптимальним планом  -крокового процесу
-крокового процесу  , що дорівнює
, що дорівнює  . Припустимо протилежне, тобто що вектор
. Припустимо протилежне, тобто що вектор  . Тоді дістанемо:
. Тоді дістанемо: ,
,
 ,
, в
в 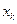 ,щоб сума витрат була найменшою.
,щоб сума витрат була найменшою. ,що лежить на діагоналі.До цієї точки можна попасти по 3 шляхах
,що лежить на діагоналі.До цієї точки можна попасти по 3 шляхах



