
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Математичні перетворення задачі динамічного програмування у диференційованій та стохастичній постановці.Содержание книги
Поиск на нашем сайте
Типову задачу математичного програмування в детермінованій постановці формулюють так: визначити вектор
Якщо функції в даній задачі крім керованих параметрів Х залежать ще і від деяких випадкових величин
де Ω — простір подій ω. Залежно від можливості отримати та врахувати інформацію стосовно детермінованості (стохастичності) функцій I) стохастичні коефіцієнти цільової функції та детерміновані обмеження; II) детерміновані коефіцієнти цільової функції та стохастичні вільні члени і коефіцієнти системи обмежень; III) стохастичні коефіцієнти цільової функції, вільні члени і коефіцієнти системи обмежень. Конкретні постановки задач стохастичного програмування мають свою специфіку. Передусім необхідно визначити: 1. Детермінованим чи випадковим є вектор Х. Якщо вектор Х є детермінованим, то він не залежить від випадкових параметрів моделі. Якщо ж він випадковий, то тоді Х є функцією від ω — 2. Як розуміти максимізацію (мінімізацію) цільової функції — як абсолютну (для всіх значень 3. Як виконуються обмеження: абсолютно для всіх При постановці задач стохастичного програмування необхідно виходити не лише з математичних міркувань, а й з економічного змісту та з врахуванням евристичних міркувань. Наприклад, детермінованість чи стохастичність вектора Х зумовлюється сутністю економічних, технологічних процесів тощо. Для сільськогосподарського підприємства, наприклад, вектор, що визначатиме площі посіву сільськогосподарських культур, обов’язково має бути детермінованим. Якщо ж шуканий вектор для того самого підприємства за тих самих умов визначатиме, приміром, обсяги кредитів, то його компоненти мають бути стохастичними величинами, бо достеменно невідомо, чи вони будуть отримані. Методи розв’язування стохастичних задач поділяють на дві групи — прямі та непрямі. Прямі методи використовують для розв’язування задач стохастичного програмування, коли існують способи побудови функцій Метод визначення коефіцієнтів рівняння регресії. 53.Яка формула відображає суть методу найменших квадратів. Разом. Для МНК шукаються такі числ. знач. параметрів р-ня, щоб сума квадратів залишків регресії була найменшою. Короткий запис Σei2=Σ(yi-b0-b1xi)2→min. На підставі теореми про необхідні умови існування екстремуму і після деяких перетворень отримуємо сист. лінійних алгебраїчних р-нь. Σyi= b0n+ b1Σxi Σxiyi=b0Σxi+ b1Σxi2 При використ. МНК до похибок εі діють вимоги(умови Гауса-Маркова).1) εі –випадкова змінна; 2)М(εі)=0; 3)дисперсія εі постійна D(εі)= D(εj)=σ2; 4)знач. εі незалежні між собою; 5)величини εі статист. незалежні зі знач. хі. Якщо виконуються, то оцінки незміщені, тобто мат.спод.= справжнім знач., ефективні (дисперсія найменша) та обґрунтовані. Узагальнений МНК (методу Ейткена) застосовується, якщо наявна гетероскедастичність. Для її визнач.вдаються до 4 критеріїв: 1)критерій μ(коли вихідна сукупність спостережень досить велика); 2)параметричний тест Гольдфельда- Квандта (сукупність спост.невелика); 3)непараметричний тест Г.-Кв.(на основі графіка зміни залишків після упорядкування спостережень за тією поясн.змінною,що може призвести до гетероскедастичності); 4)тест Глей сера (будується регресій не р-ня від тієї пояснюючої змінної, що може призвести до гетероскедастичності, тобто відповідає зміні дисперсії залишків).
|
||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 440; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.33 (0.006 с.) |

 , для компонент якого:
, для компонент якого: ,
,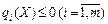 ,
, .
. , то маємо задачу стохастичного програмування:
, то маємо задачу стохастичного програмування: ,
, ,
, ,
, ,
,  постановки задач стохастичного програмування можуть містити:
постановки задач стохастичного програмування можуть містити: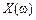 , тобто залежить від випадкових змінних.
, тобто залежить від випадкових змінних. на базі інформації щодо параметра ω. Непрямими є методи зведення стохастичної задачі до задачі лінійного чи нелінійного програмування, тобто перехід до детермінованого аналога задачі стохастичного програмування.
на базі інформації щодо параметра ω. Непрямими є методи зведення стохастичної задачі до задачі лінійного чи нелінійного програмування, тобто перехід до детермінованого аналога задачі стохастичного програмування.


