
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Необхідні і достатні умови для оптимального розв’язку двоїстої задачіСодержание книги
Поиск на нашем сайте Кожну з двох спряжених задач можна розв’язати окремо, проте встановлені теоремами двоїстості залежності між оптимальними планами прямої та двоїстої задач уможливлюють знаходження розв’язку двоїстої задачі за наявності оптимального плану прямої, і навпаки/ Приклад: До заданої задачі лінійного програмування записати двоїсту задачу. Розв’язати одну з них симплекс-методом та визначити оптимальний план другої задачі, використовуючи співвідношення першої теореми двоїстості. max Z = – 5 x1 + 2 x2;
Розв’язання. Перш ніж записати двоїсту задачу, необхідно пряму задачу звести до стандартного вигляду. Оскільки цільова функція F максимізується і в системі обмежень є нерівності, то їх слід звести до виду « max Z = – 5 x1 + 2 x2;
Тепер за відповідними правилами складемо двоїсту задачу: min F = – y1 + 5 y2;
Оскільки записані задачі симетричні, то будь-яку з них можна розв’язати симплекс-методом. Наприклад, визначимо спочатку оптимальний план прямої задачі. Для цього застосуємо алгоритм симплекс-методу. 1. max Z = – 5 x1 + 2 x2 + 0 x3 + 0 x4;
2. Векторна форма запису системи обмежень має вигляд:
де У системі векторів для утворення початкового одиничного базису відсутній один вектор. Тому введемо штучну змінну в перше обмеження. 3. Розширена задача лінійного програмування буде такою: max Z = – 5 x1 + 2 x2 + 0 x3 + 0 x4 – М x5;
У цій задачі х 4 та х 5 — базисні змінні, а х1, х2, х3 — вільні. Нехай х1 = х2 = х3 = 0, тоді х4 = 5; х5 = 1. Перший опорний план задачі: X0 = (0; 0; 0; 5; 1), Z0 = – M. 4. Подальше розв’язування прямої задачі подано у вигляді симплексної таблиці:
З останньої симплекс-таблиці запишемо оптимальний план прямої задачі: Х* = (0; 5/3; 2/3; 0), Z max = 10/3. Згідно зі співвідношенням двоїстості за першою теоремою можна висновувати, що оптимальний план двоїстої задачі існує і min F = max Z = 10/3. Компоненти вектора Y * (оптимальний план двоїстої задачі) визначимо за формулою:
де
Матриця D– 1 також міститься в останній симплекс-таблиці у стовпчиках змінних «x5» та «x4», які утворювали початковий базис. Отже,
min F = – 1 × 0 + 5 × 2/3 = 10/3. Застосувавши для розв’язування прямої задачі симплекс-метод, ми знайшли її оптимальний план, а потім визначили оптимальний розв’язок двоїстої задачі за допомогою співвідношень першої теореми двоїстості. 19. Теореми двоїстості, які дозволяють знайти розв’язок прямої задачі ЛП Теорема (перша теорема двоїстості). Якщо пряма задача має оптимальній розв’язок, то і двоїста задача має оптимальний розв’язок і навпаки. Якщо пряма задача не має оптимального розв’язку, то і двоїста задача не має оптимального розв’язку. Якщо X0 – оптимальній розв’язок прямої задачі, а Y0 – оптимальний розв’язок двоїстої задачі, то справедлива слідуюча рівність: Економічний зміст першої теореми двоїстості. Максимальний прибуток ( ЯКщо пряма задача має оптимальній розвязок і він знайдений за допомогою симплекс методу, то оптимальний розвязок двоїстої задачі можна знайти не розвязуючи її використавши слідуючу формулу: де
Теорема (друга теорема двоїстості для симетричних задач).
Для того, щоб плани X* та Y* відповідних спряжених задач були оптимальними, необхідно і достатньо, щоб виконувалися умови доповнюючої нежорсткості:
Наслідок. Якщо в результаті підстановки оптимального плану однієї із задач (прямої чи двоїстої) в систему обмежень цієї задачі і-те обмеження виконується як строга нерівність, то відповідна і-та компонента оптимального плану спряженої задачі дорівнює нулю. Економічний зміст другої теореми двоїстості стосовно оптимального плану Якщо для виготовлення всієї продукції в обсязі, який визначається оптимальним планом Економічний зміст другої теореми двоїстості стосовно оптимального плану Якщо деяке j-те обмеження виконується як нерівність, тобто всі витрати на виробництво одиниці j-го виду продукції перевищують її ціну ? Теорема (третя теорема двоїстості). Компоненти оптимального плану двоїстої задачі Економічний зміст третьої теореми двоїстості. Двоїсті оцінки є унікальним інструментом, який дає змогу зіставляти непорівнянні речі. Очевидно, що неможливим є просте зіставлення величин, які мають різні одиниці вимірювання. Якщо взяти як приклад виробничу задачу, то цікавим є питання: як змінюватиметься значення цільової функції (може вимірюватися в грошових одиницях) за зміни обсягів різних ресурсів (можуть вимірюватися в тоннах, м2, люд./год, га тощо). Використовуючи третю теорему двоїстості, можна легко визначити вплив на зміну значення цільової функції збільшення чи зменшення обсягів окремих ресурсів: числові значення двоїстих оцінок показують, на яку величину змінюється цільова функція за зміни обсягу відповідного даній оцінці ресурсу
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 445; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.33 (0.007 с.) |


 ». Тому перше обмеження задачі помножимо на (–1). Після цього знак нерівності зміниться на протилежний. Отримаємо:
». Тому перше обмеження задачі помножимо на (–1). Після цього знак нерівності зміниться на протилежний. Отримаємо:


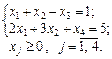
 ,
, ,
,  ,
,  ,
,  ,
,  .
.
 x5 x4
x5 x4
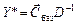 ,
, та міститься в стовпчику «сбаз» останньої симплекс-таблиці;
та міститься в стовпчику «сбаз» останньої симплекс-таблиці; .
. ,
,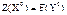 .
. ) підприємство отримує при виробництві продукції за оптимальним планом
) підприємство отримує при виробництві продукції за оптимальним планом 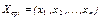 , однак ту саму суму коштів (
, однак ту саму суму коштів ( ) воно може отримати реалізуючи ресурси за оптимальними цінами
) воно може отримати реалізуючи ресурси за оптимальними цінами  . За умов використання інших планів
. За умов використання інших планів  , виходячи з основної нерівності теорії двоїстості, доходи від реалізації продукції завжди менші ніж витрати на її виробництво.
, виходячи з основної нерівності теорії двоїстості, доходи від реалізації продукції завжди менші ніж витрати на її виробництво.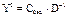 ,
, – це значення стовпчика
– це значення стовпчика 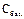 в останній симплекс таблиці.
в останній симплекс таблиці. – це матриця, яка знаходиться в останній симплекс таблиці під одиничною матрицею першої симплекс таблиці.
– це матриця, яка знаходиться в останній симплекс таблиці під одиничною матрицею першої симплекс таблиці.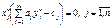

 прямої задачі.
прямої задачі. , витрати одного і-го ресурсу строго менші, ніж його загальний обсяг
, витрати одного і-го ресурсу строго менші, ніж його загальний обсяг  , то відповідна оцінка такого ресурсу
, то відповідна оцінка такого ресурсу  =0 (такий ресурс для виробництва не є цінним). Якщо ж витрати ресурсу дорівнюють його наявному обсягу, тобто його використано повністю, то він є цінним для виробництва, і його оцінка буде строго більшою від 0.
=0 (такий ресурс для виробництва не є цінним). Якщо ж витрати ресурсу дорівнюють його наявному обсягу, тобто його використано повністю, то він є цінним для виробництва, і його оцінка буде строго більшою від 0. двоїстої задачі.
двоїстої задачі. , виробництво такого виду продукції є недоцільним, і в оптимальному плані прямої задачі обсяг такої прродукції
, виробництво такого виду продукції є недоцільним, і в оптимальному плані прямої задачі обсяг такої прродукції  =0. Якщо витрати на виробництво j-го виду продукції дорівнюють ціні одиниці продукції
=0. Якщо витрати на виробництво j-го виду продукції дорівнюють ціні одиниці продукції  дорівнюють значенням частинних похідних від цільової функції
дорівнюють значенням частинних похідних від цільової функції  за відповідними аргументами
за відповідними аргументами  , або
, або  (1)
(1) .
.


