
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Причини, що зумовлюють необхідність моделювання.Содержание книги
Поиск на нашем сайте
Визначення моделі. Моделлю (від лат. - зразком) деякої системи називається штучна система абооб'єкт, що в певних умовах може замінити систему-оригінал (об'єкт) шляхом відтвореннявластивостей іхарактеристик оригіналу, які цікавлять дослідника, колитака заміна дає істотні переваги йу зручності дослідження. Таким чином, модель - це: представленняоб'єкта, системи чи ідеї в певній формі, що відрізняється відреальної, а головною характеристикою кожної моделі можнавважати спрощенняреальної ситуації в економіці, техніці чи технології, упр-нні і т. п. Допричин, якізумовлюють необхідність використання моделей належать не тільки складність прийняття управлінських рішень в реальних умовах, а й необхідність прогнозування майбутніх результатів, що ніякнеможливо зробити на оригіналі, навіть нескладному.Трапляються також ситуації, коли бажано випробувати йекспериментально перевірити деякі альтернативні варіанти вирішення проблеми. Останнє особливо стосується нових проектів чи дослідних зразків техніки. Моделювання - це систематизований засіб побачити варіанти майбутнього івизначити потенційні наслідки від альтернативних рішень. З означення слідує, що модель є широким поняттям. Для одного й того ж об'єкта можуть бути потрібнірізні моделі бо переслідуються різні цілі при дослідженні таприйняті рішень. З точки зору прийняття рішень з різногороду економічних проблем намікро- макрорівнях використовують аналогове та символічне моделюванні. Аналогова модель імітує досліджуванийоб'єкт певним графіком чи схемою. Наприклад, вибудовуючиорганізаційну структуру підприємства, керівники легко можуть уявити проходження як наказів, так і формальне підпорядкування своїх підлеглих. Графік обсяги виробництва - витрати " дає можливість не тільки оцінити залежність однієї величини від іншої, а й визначити тойкритичний обсяг виробництва певного виду продукції, нижче якого підприємству не вигідно виробляти цю продукцію через збитки. У символічній (математичній) моделі використовуються формули дляопису характеристикчи властивостей об'єкта. Цей тип моделей найчастіше використовується на практиці. Наприклад, проста формула коефіцієнта фондовіддачі є економічноюмоделлю продуктивності роботи обладнаннязапевни, період часу по підприємству. Причини, що зумовлюють необхідність моделювання. У всі періоди історії НТП складність завдань накопичення та обробки необхідної інформації, математичного моделювання та прийняття оптимальних рішень у всіх галузях суспільного виробництва зростала швидше, ніж усі інші виробничі показники, зокрема кількість людей, зайнятих розв'язанням таких завдань. Ця закономірність спричиняється постійним зростанням економічних взаємозв'язків між господарськими ланками, науково-технічною складовою, прогресом самого виробництва і, як наслідок, — постійним зростанням кількості та складності інформації, у результаті обробки та осмислення котрої приймаються адекватні рішення а саме: 1)Складність прийняття рішень в реальних умовах. 2) Необхідність прогнозування майбутніх результатів. 3)Необхідність перевірки альтернативних варіантів управлінських рішень. 4)складністю реального світу, виробничо-господарської діяльності; 5)наявністю багатофакторних залежностей у процесі розв’язання управлінських завдань; 6)необхідністю експериментальної перевірки альтернативних управлінських рішень; 7)доцільністю орієнтувати управління на майбутнє. Моделювання направлене на синтез результатів аналітичного пізнання, внаслідок чого описуються загальні закони і закономірності, стабільні властивості елементів і зв'язків у процесі функціонування або розвитку досліджуваного явища. Моделювання є основною і неодмінною умовою розвитку аналізу.
3.Поняття процесу моделювання. Процес математичного моделювання можна поділити на чотири етапи. Перший етап — формулювання законів, за якими зв'язуються між собою основні об'єкти моделі. Він вимагає широкого знання фактів відносно досліджуваного явища і глибокого проникнення в їх взаємозв'язок. Як правило, досліджуване явище супроводжується великою кількістю взаємодій між багатьма об'єктами явища. Простежити за всіма об'єктами і зв'язками між ними дуже важко й громіздко. Тому досліднику необхідно виділити основні об'єкти і основні взаємодії між ними для того, щоб математична модель була доступною для подальшого вивчення. Цей етап завершується записом у математичній формі сформульованих якісних уявлень про зв'язки між об'єктами моделі. Другий етап — дослідження математичних задач, до яких зводиться математична модель. Основним тут є розв'язування прямої задачі, тобто одержання в результаті аналізу моделі вихідних даних для подальшого їх зіставлення з результатами спостережень досліджуваного явища. На цьому етапі важливу роль відіграє математичний апарат, необхідний для аналізу математичної моделі, і обчислювальна техніка — потужний засіб для одержання кількісної вихідної інформації як результату розв'язування складних математичних задач. При цьому широко застосовуються методи обчислювальної математики. Отже, на цьому етапі дослідник повинен вибрати перш за все апарат для розв'язання сформульованої на першому етапі математичної задачі, а потім розробити алгоритм розв'язання задачі на ПЕОМ. Третій етап — перевірка, чи задовольняє прийнята гіпотетична модель критерій практики, тобто перевірка, чи узгоджуються результати спостережень з теоретичними наслідками моделі в межах точності спостережень. Якщо відхилення виходять за межі точності спостережень, то модель не може бути прийнятою. Часто при побудові моделі деякі її характеристики залишаються невизначеними. Задачі, в яких визначаються характеристики моделі таким чином, щоб вихідна інформація була порівняною в межах точності спостережень з результатами спостережень досліджуваних явищ, називаються оберненими задачами. Якщо математична модель така, що ні при якому виборі характеристик ці умови не можна задовольнити, то модель неприйнятна для дослідження цих явищ. Застосування критерію практики для оцінки математичної моделі дозволяє робити висновок про правильність положень, які лежать в основі моделі, яку треба вивчати. Цей метод є єдиним методом вивчення не доступних нам безпосередньо явищ макро- і мікросвіту. Четвертий етап — подальший аналіз моделі в зв'язку з накопиченням даних про досліджувані явища і модернізація моделі. У процесі розвитку науки і техніки дані про досліджувані явища все більше і більше уточнюються і наступає момент, коли висновки, одержані на основі існуючої математичної моделі, не відповідають нашим знанням про явище. Тоді виникає необхідність побудови нової більш досконалої математичної моделі. Таблиця 6.1
Змінні Розглянемо довільний оптимальний план
Виразимо коефіцієнти при змінних даного рівняння у вигляді суми їх цілої та дробової частин. Введемо позначення:
або
Отже, рівняння (6.11) виконується для будь-якого допустимого плану задачі (6.5)—(6.7). Допустимо тепер, що розглянутий план
де N — деяке ціле число. Величина N не може бути від’ємною. Якщо б
Звідки Якщо від лівої частини рівняння (6.12) відняти деяке невід’ємне число, то приходимо до нерівності:
[1] Цілою частиною числа а називається найбільше ціле число для яка виконується за допущенням для будь-якого цілочислового плану задачі (6.5)—(6.7). У такий спосіб виявилося, що нерівність (6.13) є шуканим правильним відтинанням. Отже, для розв’язування цілочислових задач лінійного програмування (6.1)—(6.4) методом Гоморі застосовують такий алгоритм: 1. Симплексним методом розв’язується задача без вимог цілочисловості змінних — (6.1)—(6.3). Якщо серед елементів умовно-оптимального плану немає дробових чисел, то цей план є розв’язком задачі цілочислового програмування (6.1)—(6.4). Якщо задача (6.1)—(6.3) не має розв’язку (цільова функція необмежена, або система обмежень несумісна), то задача (6.1) — (6.4) також не має розв’язку. 2. Коли в умовно-оптимальному плані є дробові значення, то вибирається змінна, яка має найбільшу дробову частину. На базі цієї змінної (елементів відповідного рядка останньої симплексної таблиці, в якому вона міститься) будується додаткове обмеження Гоморі:
3. Додаткове обмеження після зведення його до канонічного вигляду і введення базисного елемента приєднується до останньої симплексної таблиці, яка містить умовно-оптимальний план. Отриману розширену задачу розв’язують і перевіряють її розв’язок на цілочисловість. Якщо він не цілочисловий, то процедуру повторюють, повертаючись до п. 2. Так діють доти, доки не буде знайдено цілочислового розв’язку або доведено, що задача не має допустимих розв’язків на множині цілих чисел. У літературі [12, 27] доведено, що за певних умов алгоритм Гоморі є скінченним, але процес розв’язування задач великої розмірності методом Гоморі повільно збіжний. Слід також мати на увазі, що і кількість ітерацій суттєво залежить від сформованого правильного відтинання. Наведене правило (6.13) щодо формування правильного відтинання не єдине. Існують ефективніші відтинання, які використовуються у другому та третьому алгоритмах Гоморі [12, 27], однак наявний практичний досвід ще не дає змоги виділити з них найкращий. Загалом, алгоритм Гоморі в обчислювальному аспекті є мало вивченим. Якщо в лінійному програмуванні спостерігається відносно жорстка залежність між кількістю обмежень задачі та кількістю ітерацій, що необхідна для її розв’язування, то для цілочислових задач такої залежності не існує. Кількість змінних також мало впливає на трудомісткість обчислень. Очевидно, процес розв’язання цілочислової задачі визначається не лише її розмірністю, а також особливостями багатогранника допустимих розв’язків, що являє собою набір ізольованих точок. Як правило, розв’язування задач цілочислового програмування потребує великого обсягу обчислень. Тому при створенні програм для ЕОМ особливу увагу слід приділяти засобам, що дають змогу зменшити помилки округлення, які можуть призвести до того, що отриманий цілочисловий план не буде оптимальним. Метод диференціальних рент. Якщо при визначенні оптимального плану транспортної задачі методом потенціалів спочатку перебував який-небудь її опорний план, а потім він послідовно поліпшувався, то при знаходженні вирішення транспортної задачі методом диференціальних рент спочатку найкращим чином розподіляють між пунктами призначення частина вантажу (так зване умовно оптимальний розподіл) і на ітераціях поступово зменшують загальну величину нерозподілених поставок. Початковий варіант розподілу товару виділяють таким чином. В кожному із стовбців таблиці даних ТЗ знаходять мінімальний тариф. Знайдені числа обводять кружечком, а клітинки, в яких знаходяться вказані числа, заповнюють. В них записують максимально можливі числа. В результаті отримують деякі розподілення поставок вантажу в місцях призначення. Цей розподіл в даному випадку не задовольняє обмеженням вихідної ТЗ. Тому в результаті наступних кроків потрібно поступово зменшувати не розподілені поставки вантажу так, щоби при цьому загальна вартість перевезень залишалася мінімальною. Для цього спочатку виділяють збиткові і неостаточні рядки. Рядки, які відповідають поставникам, запаси яких повністю розподілені, а потреби пункту призначення, зв'язаних з даними потребами запланованими поставками, не задовільнені, недостатними. Ці рядки деколи називають також від'ємними. Рядки, запаси яких вичерпані не повністю, рахуються збитковими. Деколи їх називають також додатними. Після деякого числа описаних вище ітерацій нерозподілений залишок стає рівним нулю. В результаті отримують оптимальний план даної ТЗ. Описаний вище метод розв'язання ТЗ має більш просту логічну схему розрахунків, чим розглянутий вище метод потенціалів. Тому в більшості випадків для знаходження розв'язку конкретних ТЗ з використанням ЄВМ використовують метод диференціальних рент.
31.Суть методу потенціалів. Метод потенціалів дозволяє, виходячи з деякого опорного плану перевезень, побудувати за скінчене число ітерацій рішення транспортної задачі шляхом послідовного переходу від опорного плану до оптимального. Загальна схема методу така. У даному початковому опорному плані кожному пункту ставлять у відповідність деяке число, яке називається його попереднім потенціалом. Попередні потенціали обирають так, щоб їх різниця для будь-якої пари пунктів Аi и Вj, пов’язаних основною комунікацією, дорівнювала сij. Якщо відбудеться так, що різниця попередніх потенціалів для всіх інших комунікацій не перевищує сij, то даний план перевезень – оптимальне рішення задачі. У противному випадку вказують спосіб покращення опорного плану транспортної задачі. Теорема Куна-Такера. Теорема Куна—Таккера дає змогу встановити типи задач, для яких на множині допустимих розв’язків існує лише один глобальний екстремум зумовленого типу. Вона тісно пов’язана з необхідними та достатніми умовами існування сідлової точки. Розглянемо задачу нелінійного програмування, яку, не зменшуючи загальності, подамо у вигляді:
(Очевидно, що знак нерівності можна змінити на протилежний множенням лівої і правої частин обмеження на (– 1)). Теорема 8.1. (Теорема Куна—Таккера). Вектор Х* є оптимальним розв’язком задачі (8.22)—(8.24) тоді і тільки тоді, коли існує такий вектор
і функція мети Доведення. Необхідність. Нехай Х* — оптимальний план задачі (8.22)—(8.24), тобто є точкою глобального максимуму задачі. Отже, для всіх інших планів задачі Х з множини допустимих розв’язків виконуватиметься співвідношення:
Розглянемо тепер вектор З умови (8.21) маємо:
Для точки з координатами
Функція Для встановлення нерівності, що відповідає лівій частині умови (8.13), а саме:
Отже, у точці Х * функція Лагранжа має глобальний максимум по Х, що повністю доводить необхідність теореми. Достатність. Для доведення достатності умов теореми потрібно виходити з того, що Підставимо у нерівність (8.13) вираз функції Лагранжа (8.12) для задачі (8.22)—(8.23):
при всіх значеннях Розглянемо праву частину подвійної нерівності (8.26).
Остання нерівність має виконуватися для всіх
Тоді з лівої частини нерівності (8.26) маємо:
Через те що Отже, точка Х * задовольняє обмеження і надає максимального значення цільовій функції задачі, тому що для всіх інших Рис.3.6.1- Методика аналізу проблеми з використанням дерева цілей Для оцінки очікуваної віддачі (або інший термін – післядії, а це може бути, наприклад, прибуток/збиток) використовується процедура, що має назву “зворотна індукція“. На вилці дій вибирається та гілка, яка має найбільше значення для очікуваної віддачі. Правостороння вилка дій (“не купувати” виключається) перекреслюється подвійною лінією. Починаючи праворуч від дерева, рухаємося над вузлами рішень. Очікуваною цінністю досконалої інформації (Expected Value Perfect Information) називається різниця між очікуваною віддачею (від рішення) в умовах визначеності та в умовах ризику:

Щоб визначити очікувану цінність в умовах визначеності, обираємо найкращу альтернативу для кожного стану природи і викликану нею віддачу перемножуємо на ймовірність появи цього стану природи:
Визначення моделі. Моделлю (від лат. - зразком) деякої системи називається штучна система абооб'єкт, що в певних умовах може замінити систему-оригінал (об'єкт) шляхом відтвореннявластивостей іхарактеристик оригіналу, які цікавлять дослідника, колитака заміна дає істотні переваги йу зручності дослідження. Таким чином, модель - це: представленняоб'єкта, системи чи ідеї в певній формі, що відрізняється відреальної, а головною характеристикою кожної моделі можнавважати спрощенняреальної ситуації в економіці, техніці чи технології, упр-нні і т. п. Допричин, якізумовлюють необхідність використання моделей належать не тільки складність прийняття управлінських рішень в реальних умовах, а й необхідність прогнозування майбутніх результатів, що ніякнеможливо зробити на оригіналі, навіть нескладному.Трапляються також ситуації, коли бажано випробувати йекспериментально перевірити деякі альтернативні варіанти вирішення проблеми. Останнє особливо стосується нових проектів чи дослідних зразків техніки. Моделювання - це систематизований засіб побачити варіанти майбутнього івизначити потенційні наслідки від альтернативних рішень. З означення слідує, що модель є широким поняттям. Для одного й того ж об'єкта можуть бути потрібнірізні моделі бо переслідуються різні цілі при дослідженні таприйняті рішень. З точки зору прийняття рішень з різногороду економічних проблем намікро- макрорівнях використовують аналогове та символічне моделюванні. Аналогова модель імітує досліджуванийоб'єкт певним графіком чи схемою. Наприклад, вибудовуючиорганізаційну структуру підприємства, керівники легко можуть уявити проходження як наказів, так і формальне підпорядкування своїх підлеглих. Графік обсяги виробництва - витрати " дає можливість не тільки оцінити залежність однієї величини від іншої, а й визначити тойкритичний обсяг виробництва певного виду продукції, нижче якого підприємству не вигідно виробляти цю продукцію через збитки. У символічній (математичній) моделі використовуються формули дляопису характеристикчи властивостей об'єкта. Цей тип моделей найчастіше використовується на практиці. Наприклад, проста формула коефіцієнта фондовіддачі є економічноюмоделлю продуктивності роботи обладнаннязапевни, період часу по підприємству. Причини, що зумовлюють необхідність моделювання. У всі періоди історії НТП складність завдань накопичення та обробки необхідної інформації, математичного моделювання та прийняття оптимальних рішень у всіх галузях суспільного виробництва зростала швидше, ніж усі інші виробничі показники, зокрема кількість людей, зайнятих розв'язанням таких завдань. Ця закономірність спричиняється постійним зростанням економічних взаємозв'язків між господарськими ланками, науково-технічною складовою, прогресом самого виробництва і, як наслідок, — постійним зростанням кількості та складності інформації, у результаті обробки та осмислення котрої приймаються адекватні рішення а саме: 1)Складність прийняття рішень в реальних умовах. 2) Необхідність прогнозування майбутніх результатів. 3)Необхідність перевірки альтернативних варіантів управлінських рішень. 4)складністю реального світу, виробничо-господарської діяльності; 5)наявністю багатофакторних залежностей у процесі розв’язання управлінських завдань; 6)необхідністю експериментальної перевірки альтернативних управлінських рішень; 7)доцільністю орієнтувати управління на майбутнє. Моделювання направлене на синтез результатів аналітичного пізнання, внаслідок чого описуються загальні закони і закономірності, стабільні властивості елементів і зв'язків у процесі функціонування або розвитку досліджуваного явища. Моделювання є основною і неодмінною умовою розвитку аналізу.
3.Поняття процесу моделювання. Процес математичного моделювання можна поділити на чотири етапи. Перший етап — формулювання законів, за якими зв'язуються між собою основні об'єкти моделі. Він вимагає широкого знання фактів відносно досліджуваного явища і глибокого проникнення в їх взаємозв'язок. Як правило, досліджуване явище супроводжується великою кількістю взаємодій між багатьма об'єктами явища. Простежити за всіма об'єктами і зв'язками між ними дуже важко й громіздко. Тому досліднику необхідно виділити основні об'єкти і основні взаємодії між ними для того, щоб математична модель була доступною для подальшого вивчення. Цей етап завершується записом у математичній формі сформульованих якісних уявлень про зв'язки між об'єктами моделі. Другий етап — дослідження математичних задач, до яких зводиться математична модель. Основним тут є розв'язування прямої задачі, тобто одержання в результаті аналізу моделі вихідних даних для подальшого їх зіставлення з результатами спостережень досліджуваного явища. На цьому етапі важливу роль відіграє математичний апарат, необхідний для аналізу математичної моделі, і обчислювальна техніка — потужний засіб для одержання кількісної вихідної інформації як результату розв'язування складних математичних задач. При цьому широко застосовуються методи обчислювальної математики. Отже, на цьому етапі дослідник повинен вибрати перш за все апарат для розв'язання сформульованої на першому етапі математичної задачі, а потім розробити алгоритм розв'язання задачі на ПЕОМ. Третій етап — перевірка, чи задовольняє прийнята гіпотетична модель критерій практики, тобто перевірка, чи узгоджуються результати спостережень з теоретичними наслідками моделі в межах точності спостережень. Якщо відхилення виходять за межі точності спостережень, то модель не може бути прийнятою. Часто при побудові моделі деякі її характеристики залишаються невизначеними. Задачі, в яких визначаються характеристики моделі таким чином, щоб вихідна інформація була порівняною в межах точності спостережень з результатами спостережень досліджуваних явищ, називаються оберненими задачами. Якщо математична модель така, що ні при якому виборі характеристик ці умови не можна задовольнити, то модель неприйнятна для дослідження цих явищ. Застосування критерію практики для оцінки математичної моделі дозволяє робити висновок про правильність положень, які лежать в основі моделі, яку треба вивчати. Цей метод є єдиним методом вивчення не доступних нам безпосередньо явищ макро- і мікросвіту. Четвертий етап — подальший аналіз моделі в зв'язку з накопиченням даних про досліджувані явища і модернізація моделі. У процесі розвитку науки і техніки дані про досліджувані явища все більше і більше уточнюються і наступає момент, коли висновки, одержані на основі існуючої математичної моделі, не відповідають нашим знанням про явище. Тоді виникає необхідність побудови нової більш досконалої математичної моделі.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 492; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.238.67 (0.013 с.) |

 — базисні, а
— базисні, а  — вільні. Оптимальний план задачі:
— вільні. Оптимальний план задачі:  . Якщо
. Якщо  — цілі числа, то отриманий розв’язок є цілочисловим оптимальним планом задачі (6.5)—(6.8). Інакше існує хоча б одне з чисел, наприклад,
— цілі числа, то отриманий розв’язок є цілочисловим оптимальним планом задачі (6.5)—(6.8). Інакше існує хоча б одне з чисел, наприклад,  — дробове. Отже, необхідно побудувати правильне обмеження, що відтинає нецілу частину значення
— дробове. Отже, необхідно побудувати правильне обмеження, що відтинає нецілу частину значення 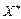 задачі (6.5) —(6.7). Виразимо в цьому плані базисну змінну
задачі (6.5) —(6.7). Виразимо в цьому плані базисну змінну  через вільні змінні:
через вільні змінні: . (6.9)
. (6.9) — ціла частина числа b,
— ціла частина числа b,  — дробова частина числа b [1]. Отримаємо:
— дробова частина числа b [1]. Отримаємо: , (6.10)
, (6.10) . (6.11)
. (6.11) , (6.12)
, (6.12)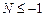 , то з рівняння (6.12) приходимо до нерівності:
, то з рівняння (6.12) приходимо до нерівності: .
. . Тобто це означало б, що дробова частина
. Тобто це означало б, що дробова частина  перевищує одиницю, що неможливо. У такий спосіб доведено, що число N є невід’ємним.
перевищує одиницю, що неможливо. У такий спосіб доведено, що число N є невід’ємним. , (6.13)
, (6.13)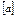 , що не перевищує а. Дробовою частиною є число
, що не перевищує а. Дробовою частиною є число  , яке дорівнює різниці між самим числом а та його цілою частиною, тобто
, яке дорівнює різниці між самим числом а та його цілою частиною, тобто  . Наприклад, для
. Наприклад, для 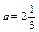
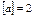 ,
,  ;
;
 ,
,  .
. .
. , (8.22)
, (8.22) , (8.23)
, (8.23) . (8.24)
. (8.24) , що при
, що при  для всіх
для всіх  точка
точка 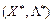 є сідловою точкою функції Лагранжа
є сідловою точкою функції Лагранжа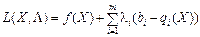 ,
, для всіх
для всіх  угнута, а функції
угнута, а функції  — опуклі.
— опуклі.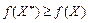 .
. , що відповідає точці глобального максимуму
, що відповідає точці глобального максимуму 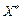 , і значення функції Лагранжа в точках
, і значення функції Лагранжа в точках  ,
,  ,
,  , де
, де  — вектор множників Лагранжа, що відповідає Х.
— вектор множників Лагранжа, що відповідає Х. , тоді
, тоді . (8.25)
. (8.25) можуть бути відмінними від нуля. Оскільки за умовою задачі
можуть бути відмінними від нуля. Оскільки за умовою задачі  , то лише за умови, що
, то лише за умови, що  .
. — лінійна відносно
— лінійна відносно  , тобто остання нерівність виконується для будь-якого
, тобто остання нерівність виконується для будь-якого  — точка глобального мінімуму по
— точка глобального мінімуму по  , скористаємося також рівнянням (8.21), підсумувавши його по і:
, скористаємося також рівнянням (8.21), підсумувавши його по і:  . За умовою теореми
. За умовою теореми  — угнуті функції і
— угнуті функції і 
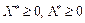 ,
,  — сідлова точка функції
— сідлова точка функції  (тобто для
(тобто для  (8.26)
(8.26) .
.


 .
. , тобто нерівність справджується лише у разі, коли
, тобто нерівність справджується лише у разі, коли .
.
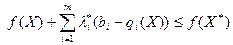 .
. , приходимо до нерівності
, приходимо до нерівності  , яка справджується для всіх значень
, яка справджується для всіх значень 



