
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формули, які складають основу реалізації двоїстого симплексного методу .Содержание книги
Поиск на нашем сайте Нехай необхідно розв’язати задачу лінійного програмування, подану в канонічному виді:
Тоді двоїстою до неї буде така задача:
алгоритм двоїстого симплексного методу: 1. Необхідно звести всі обмеження задачі до виду «£», ввести додаткові невід’ємні змінні, визначити початковий базис та перший опорний план 2. Якщо всі оцінки векторів 3. Якщо в l- му рядку, що відповідає змінній
що дає змогу вибрати вектор, який буде включено в базис. 4. Виконавши крок методу повних виключень Жордана—Гаусса, переходять до наступної симплексної таблиці (Переходять до пункту 2). Зазначимо, що для задачі знаходження максимального значення цільової функції за наведеним алгоритмом необхідно перейти до цільової функції Якщо коефіцієнт цільової функції при деякій k -ій змінній
де С, Х — відповідно вектор компонент цільової функції та вектор змінних, ek — одиничний вектор-рядок, де одиниця відповідає k -ій компоненті 22.Суть методу Гомої для розв’язку задачі цілочислового програмування. Методи відтинання. Метод Гоморі В основу методів цілочислового програмування покладено ідею Данціга. Допустимо, що необхідно розв’язувати задачу лінійного програмування, всі або частина змінних якої мають бути цілочисловими. Можливо, якщо розв’язувати задачу, не враховуючи умову цілочисловості, випадково одразу буде отримано потрібний розв’язок. Однак така ситуація малоймовірна. Переважно розв’язок не задовольнятиме умову цілочисловості. Тоді накладають додаткове обмеження, яке не виконується для отриманого плану задачі, проте задовольняє будь-який цілочисловий розв’язок. Таке додаткове обмеження називають правильним відтинанням. Система лінійних обмежень задачі доповнюється новою умовою і далі розв’язується отримана задача лінійного програмування. Якщо її розв’язок знову не задовольняє умови цілочисловості, то будується нове лінійне обмеження, що відтинає отриманий розв’язок, не зачіпаючи цілочислових планів. Процес приєднання додаткових обмежень повторюють доти, доки не буде знайдено цілочислового оптимального плану, або доведено, що його не існує.
Слід відмітити, що визначення правила для реалізації ідеї Данціга стосовно формування додаткового обмеження виявилось досить складним завданням і першим, кому вдалось успішно реалізувати цю ідею, був Гоморі. Розглянемо алгоритм, запропонований Гоморі, для розв’язування повністю цілочислової задачі лінійного програмування, що ґрунтується на використанні симплексного методу і передбачає застосування досить простого способу побудови правильного відтинання. Нехай маємо задачу цілочислового програмування:
за умов:
Допустимо, що параметри Не враховуючи умови цілочисловості, знаходимо розв’язок задачі (6.5)—(6.7) симплексним методом. Нехай розв’язок існує і міститься в такій симплексній таблиці: Таблиця 6.1
Змінні Розглянемо довільний оптимальний план
Виразимо коефіцієнти при змінних даного рівняння у вигляді суми їх цілої та дробової частин. Введемо позначення:
або
Отже, рівняння (6.11) виконується для будь-якого допустимого плану задачі (6.5)—(6.7). Допустимо тепер, що розглянутий план
де N — деяке ціле число. Величина N не може бути від’ємною. Якщо б
Звідки Якщо від лівої частини рівняння (6.12) відняти деяке невід’ємне число, то приходимо до нерівності:
[1] Цілою частиною числа а називається найбільше ціле число для яка виконується за допущенням для будь-якого цілочислового плану задачі (6.5)—(6.7). У такий спосіб виявилося, що нерівність (6.13) є шуканим правильним відтинанням. Отже, для розв’язування цілочислових задач лінійного програмування (6.1)—(6.4) методом Гоморі застосовують такий алгоритм: 1. Симплексним методом розв’язується задача без вимог цілочисловості змінних — (6.1)—(6.3). Якщо серед елементів умовно-оптимального плану немає дробових чисел, то цей план є розв’язком задачі цілочислового програмування (6.1)—(6.4). Якщо задача (6.1)—(6.3) не має розв’язку (цільова функція необмежена, або система обмежень несумісна), то задача (6.1) — (6.4) також не має розв’язку. 2. Коли в умовно-оптимальному плані є дробові значення, то вибирається змінна, яка має найбільшу дробову частину. На базі цієї змінної (елементів відповідного рядка останньої симплексної таблиці, в якому вона міститься) будується додаткове обмеження Гоморі:
3. Додаткове обмеження після зведення його до канонічного вигляду і введення базисного елемента приєднується до останньої симплексної таблиці, яка містить умовно-оптимальний план. Отриману розширену задачу розв’язують і перевіряють її розв’язок на цілочисловість. Якщо він не цілочисловий, то процедуру повторюють, повертаючись до п. 2. Так діють доти, доки не буде знайдено цілочислового розв’язку або доведено, що задача не має допустимих розв’язків на множині цілих чисел. У літературі [12, 27] доведено, що за певних умов алгоритм Гоморі є скінченним, але процес розв’язування задач великої розмірності методом Гоморі повільно збіжний. Слід також мати на увазі, що і кількість ітерацій суттєво залежить від сформованого правильного відтинання. Наведене правило (6.13) щодо формування правильного відтинання не єдине. Існують ефективніші відтинання, які використовуються у другому та третьому алгоритмах Гоморі [12, 27], однак наявний практичний досвід ще не дає змоги виділити з них найкращий. Загалом, алгоритм Гоморі в обчислювальному аспекті є мало вивченим. Якщо в лінійному програмуванні спостерігається відносно жорстка залежність між кількістю обмежень задачі та кількістю ітерацій, що необхідна для її розв’язування, то для цілочислових задач такої залежності не існує. Кількість змінних також мало впливає на трудомісткість обчислень. Очевидно, процес розв’язання цілочислової задачі визначається не лише її розмірністю, а також особливостями багатогранника допустимих розв’язків, що являє собою набір ізольованих точок. Як правило, розв’язування задач цілочислового програмування потребує великого обсягу обчислень. Тому при створенні програм для ЕОМ особливу увагу слід приділяти засобам, що дають змогу зменшити помилки округлення, які можуть призвести до того, що отриманий цілочисловий план не буде оптимальним.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 400; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.008 с.) |

 ,
, ,
, .
.
 .
.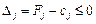 і компоненти вектора-стовпчика «План»
і компоненти вектора-стовпчика «План» 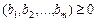 для всіх
для всіх  , то задача розв’язана. Інакше необхідно вибрати найбільшу за модулем компоненту
, то задача розв’язана. Інакше необхідно вибрати найбільшу за модулем компоненту  і відповідну змінну
і відповідну змінну 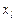 виключити з базису.
виключити з базису.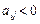 , то цільова функція двоїстої задачі необмежена на багатограннику розв’язків, а початкова задача розв’язку не має. Інакше існують деякі
, то цільова функція двоїстої задачі необмежена на багатограннику розв’язків, а початкова задача розв’язку не має. Інакше існують деякі  :
: (
( , або дещо змінити сам алгоритм
, або дещо змінити сам алгоритм  .
.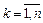 з початковим значенням
з початковим значенням  змінився на величину
змінився на величину  . Отже, цільова функція набуде вигляду:
. Отже, цільова функція набуде вигляду: ,
, Геометрично введення додаткового лінійного обмеження означає проведення гіперплощини (прямої), що відтинає від багатогранника (багатокутника) допустимих розв’язків задачі ту його частину, яка містить точки з нецілочисловими координатами, однак не торкається жодної цілочислової точки даної множини. Отриманий новий багатогранник розв’язків містить всі цілі точки, які були в початковому, і розв’язок, що буде отримано на ньому, буде цілочисловим (рис. 6.3).
Геометрично введення додаткового лінійного обмеження означає проведення гіперплощини (прямої), що відтинає від багатогранника (багатокутника) допустимих розв’язків задачі ту його частину, яка містить точки з нецілочисловими координатами, однак не торкається жодної цілочислової точки даної множини. Отриманий новий багатогранник розв’язків містить всі цілі точки, які були в початковому, і розв’язок, що буде отримано на ньому, буде цілочисловим (рис. 6.3). (6.5)
(6.5) ,
,  (6.6)
(6.6) ,
,  (6.7)
(6.7) — цілі числа
— цілі числа  . (6.8)
. (6.8) — цілі числа.
— цілі числа. — базисні, а
— базисні, а  — вільні. Оптимальний план задачі:
— вільні. Оптимальний план задачі:  . Якщо
. Якщо  — цілі числа, то отриманий розв’язок є цілочисловим оптимальним планом задачі (6.5)—(6.8). Інакше існує хоча б одне з чисел, наприклад,
— цілі числа, то отриманий розв’язок є цілочисловим оптимальним планом задачі (6.5)—(6.8). Інакше існує хоча б одне з чисел, наприклад,  — дробове. Отже, необхідно побудувати правильне обмеження, що відтинає нецілу частину значення
— дробове. Отже, необхідно побудувати правильне обмеження, що відтинає нецілу частину значення 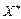 задачі (6.5) —(6.7). Виразимо в цьому плані базисну змінну
задачі (6.5) —(6.7). Виразимо в цьому плані базисну змінну  через вільні змінні:
через вільні змінні: . (6.9)
. (6.9) — ціла частина числа b,
— ціла частина числа b,  — дробова частина числа b [1]. Отримаємо:
— дробова частина числа b [1]. Отримаємо: , (6.10)
, (6.10) . (6.11)
. (6.11) , (6.12)
, (6.12)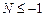 , то з рівняння (6.12) приходимо до нерівності:
, то з рівняння (6.12) приходимо до нерівності: .
. . Тобто це означало б, що дробова частина
. Тобто це означало б, що дробова частина  перевищує одиницю, що неможливо. У такий спосіб доведено, що число N є невід’ємним.
перевищує одиницю, що неможливо. У такий спосіб доведено, що число N є невід’ємним. , (6.13)
, (6.13)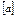 , що не перевищує а. Дробовою частиною є число
, що не перевищує а. Дробовою частиною є число  , яке дорівнює різниці між самим числом а та його цілою частиною, тобто
, яке дорівнює різниці між самим числом а та його цілою частиною, тобто  . Наприклад, для
. Наприклад, для 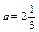
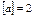 ,
,  ;
;
 ,
,  .
. .
.


