
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
З якої умови починають розв’язок транспортної задачі?Содержание книги
Поиск на нашем сайте
Теорема (умова існування розв’язку транспортної задачі): необхідною і достатньою умовою існування розв’язку транспортної задачі є її збалансованість: У розглянутій задачі має виконуватися умова:
Транспортну задачу називають збалансованою, або закритою, якщо виконується умова (5.5). Якщо ж така умова не виконується, то транспортну задачу називають незбалансованою, або відкритою. Якщо 28.Умова якою перевіряють на оптимальність базові плани транс. задачі. Оптимальним планом транспортної задачі називають матрицю Перевірка на оптимальність базисних планів здійснюється за умовою 29. Умова за якою визначають потенціали для базисних планів транспортної задачі. Оптимізація плану виконується за умови ui та vj – деякі величини які називаються потенціалами. Їх знаходять з рівняння для всіх заповнених баз кліток. ui + vj = cij. Метод диференціальних рент. Якщо при визначенні оптимального плану транспортної задачі методом потенціалів спочатку перебував який-небудь її опорний план, а потім він послідовно поліпшувався, то при знаходженні вирішення транспортної задачі методом диференціальних рент спочатку найкращим чином розподіляють між пунктами призначення частина вантажу (так зване умовно оптимальний розподіл) і на ітераціях поступово зменшують загальну величину нерозподілених поставок. Початковий варіант розподілу товару виділяють таким чином. В кожному із стовбців таблиці даних ТЗ знаходять мінімальний тариф. Знайдені числа обводять кружечком, а клітинки, в яких знаходяться вказані числа, заповнюють. В них записують максимально можливі числа. В результаті отримують деякі розподілення поставок вантажу в місцях призначення. Цей розподіл в даному випадку не задовольняє обмеженням вихідної ТЗ. Тому в результаті наступних кроків потрібно поступово зменшувати не розподілені поставки вантажу так, щоби при цьому загальна вартість перевезень залишалася мінімальною. Для цього спочатку виділяють збиткові і неостаточні рядки.
Рядки, які відповідають поставникам, запаси яких повністю розподілені, а потреби пункту призначення, зв'язаних з даними потребами запланованими поставками, не задовільнені, недостатними. Ці рядки деколи називають також від'ємними. Рядки, запаси яких вичерпані не повністю, рахуються збитковими. Деколи їх називають також додатними.
Після деякого числа описаних вище ітерацій нерозподілений залишок стає рівним нулю. В результаті отримують оптимальний план даної ТЗ. Описаний вище метод розв'язання ТЗ має більш просту логічну схему розрахунків, чим розглянутий вище метод потенціалів. Тому в більшості випадків для знаходження розв'язку конкретних ТЗ з використанням ЄВМ використовують метод диференціальних рент.
31.Суть методу потенціалів. Метод потенціалів дозволяє, виходячи з деякого опорного плану перевезень, побудувати за скінчене число ітерацій рішення транспортної задачі шляхом послідовного переходу від опорного плану до оптимального. Загальна схема методу така. У даному початковому опорному плані кожному пункту ставлять у відповідність деяке число, яке називається його попереднім потенціалом. Попередні потенціали обирають так, щоб їх різниця для будь-якої пари пунктів Аi и Вj, пов’язаних основною комунікацією, дорівнювала сij. Якщо відбудеться так, що різниця попередніх потенціалів для всіх інших комунікацій не перевищує сij, то даний план перевезень – оптимальне рішення задачі. У противному випадку вказують спосіб покращення опорного плану транспортної задачі.
|
||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 456; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.221.122 (0.007 с.) |

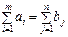 .
.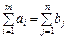 . (5.5)
. (5.5)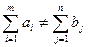 , тоді потрібно ввести додаткового (фіктивного) споживача (або постачальника) з потребою, рівною різниці ai та bj. Собівартість перевезень для цього споживача (постачальника) мають бути нульовими, що означає перевезення можливі тільки умовно.
, тоді потрібно ввести додаткового (фіктивного) споживача (або постачальника) з потребою, рівною різниці ai та bj. Собівартість перевезень для цього споживача (постачальника) мають бути нульовими, що означає перевезення можливі тільки умовно.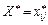
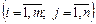 , яка задовольняє умови задачі, і для якої цільова функція набирає найменшого значення.
, яка задовольняє умови задачі, і для якої цільова функція набирає найменшого значення.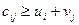 для всіх кліток, де ui і vj – потенціали, які знаходять за такими привалами. Вводять термінологію: клітка з вантажем – базисна клітка, клітка без вантажу – вільна клітка. Для базисних кліток сij = ui + vj, звідки надаючи одному з потенціалів довільного значення (наприклад 0), знаходять інші потенціали для всіх споживачів і постачальників (тобто стовпців і рядків). Значення суми потенціалів для кожної клітки проставляють у нижньому кутку клітки.
для всіх кліток, де ui і vj – потенціали, які знаходять за такими привалами. Вводять термінологію: клітка з вантажем – базисна клітка, клітка без вантажу – вільна клітка. Для базисних кліток сij = ui + vj, звідки надаючи одному з потенціалів довільного значення (наприклад 0), знаходять інші потенціали для всіх споживачів і постачальників (тобто стовпців і рядків). Значення суми потенціалів для кожної клітки проставляють у нижньому кутку клітки.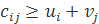 .
.


