
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основні перетворення при застосуванні методу множників Лагранжа.Содержание книги
Поиск на нашем сайте
* Приклад. Нехай треба знайти точки екстремуму функції f °(x)= x на множині x=[(x,y)? E2:x3-y2=0] Застосуємо метод множників Лагранжа. Будуємо функцію Лагранжа задачі L(x, y, λ0, λ1)=λ0x+λ1(x3-y2) та записуємо необхідні умови екстремуму:
Якщо припустити, що λ0>0, то з першого рівняння будемо мати λ0=-3λ1x2, де λ1<0. х>0. Тоді з рівняння х 3-у 2= 0 випливає, що у=0. Отже, λ1<0, у≠0 і система не буде сумісною, оскільки не задовольняється рівняння -2λ1у=0. Виходить, що система сумісна лише при λ0=0. Тоді λ1=1і розв'язком системи відносно х і убуде точка (0,0). Таким чином, задача є виродженою в точці (0,0), яка є підозрілою на екстремум. Виразивши х через у із обмеження х 3-у 2= 0, отримаємо f 0 (x)= x = у 2/3 при **Метод множників Лагранжа. Ідея методу множників Лагранжа полягає в заміні початкової задачі простішою. Для цього цільову функцію замінюють іншою, з більшою кількістю змінних, тобто такою, яка включає в себе умови, що подані як обмеження. Після такого перетворення дальше розв’язування задачі полягає в знаходженні екстремуму нової функції, на змінні якої не накладено ніяких обмежень. Тобто від початкової задачі пошуку умовного екстремуму переходимо до задачі відшукання безумовного екстремального значення іншої функції. Отже, завдяки такому перетворенню можливе застосування методів класичного знаходження екстремуму функції кількох змінних. Узагальнення необхідної умови існування локального екстремуму функції n змінних має аналогічний вигляд. Отже, для розв’язування задачі необхідно знайти вирази частинних похідних нової цільової функції за кожною змінною і прирівняти їх до нуля. В результаті отримаємо систему рівнянь. Її розв’язок визначає так звані стаціонарні точки, серед яких є і шукані екстремальні значення функції. Розглянемо метод множників Лагранжа для розв’язування задачі нелінійного програмування, що має вигляд: за умов: де функції Задача (8.6), (8.7) полягає в знаходженні екстремуму функції Переходимо до задачі пошуку безумовного екстремуму. В літературі [13, 28] теоретично доведено, що постановки та розв’язання таких задач еквівалентні. Замінюємо цільову функцію (8.6) на складнішу. Ця функція називається функцією Лагранжа і має такий вигляд:
де Знайдемо частинні похідні і прирівняємо їх до нуля:
Друга група рівнянь системи (8.9) забезпечує виконання умов (8.7) початкової задачі нелінійного програмування. Система (8.9), як правило, нелінійна. Розв’язками її є Для діагностування стаціонарних точок і визначення типу екстремуму необхідно перевірити виконання достатніх умов екстремуму, тобто дослідити в околі стаціонарних точок диференціали другого порядку (якщо для функцій Узагальнення достатньої умови існування локального екстремуму для функції n змінних приводить до такого правила: за функцією Лагранжа виду (8.8) будується матриця Гессе, що має блочну структуру розмірністю
де О — матриця розмірністю Р — матриця розмірністю
Q — матриця розмірністю
Розглянемо ознаки виду екстремуму розв’язку системи (8.9). Нехай стаціонарна точка має координати 1. Точка 2. Точка Розглянемо задачу, розв’язок якої знайдемо методом множників Лагранжа. **Для розв'язування задач нелінійного програмування не існує універсального методу, а тому доводиться застосовувати багато методів іобчислювальних алгоритмів, які ґрунтуються, здебільшого, на теорії диференціального числення, і вибір їх залежить від конкретної постановки задачі та форми економіко-математичної моделі. Методи нелінійного програмування бувають прямі та непрямі. Прямими методами оптимальні розв'язки відшукують у напрямку найшвидшого збільшення (зменшення) цільової функції. Типовими для цієї групи методів є градієнти. Непрямі методи полягають у зведенні задачі до такої, знаходження оптимуму якої вдається спростити. До них належать, насамперед, найбільш розроблені методи квадратичного та сепарабельного програмування. Оптимізаційні задачі, на змінні яких не накладаються обмеження, розв'язують методами класичної математики. Оптимізацією з обмеженнями-рівностями виконують методами зведеного градієнта, скажімо методом Якобі, та множників Лагранжа. У задачах оптимізації з обмеженнями-нерівностями досліджують необхідні та достатні умови існування екстремуму Куна—Таккера. Розглянемо метод множників Лагранжа на прикладі такої задачі нелінійного програмування: Z =f (х1, х2... хп) — > mах (min) за умов q1(x1,x2,…xn)=bi,i=1, де функція f (х1, x2,..., хп) i q1(x1, x2, …xn) диференційовані. Ідея методу множників Лагранжа полягає в заміні даної задачі простішою: на знаходження екстремуму складнішої функції, але без обмежень. Ця функція називається функцією Лагранжа і подається у вигляді
де λi— не визначені поки що величини, так звані множники Лагранжа. Знайшовши частинні похідні функції L за всіма змінними і прирівнявши їх до нуля:
запишемо систему
що є, як правило, нелінійною. Розв'язавши цю систему, знайдемо X* =(х1, x2,..., хп) i λ0= (λ1, λ 2,..., λm) — стаціонарні точки. Оскільки їх визначено з необхідної умови екстремуму, то в них можливий максимум або мінімум.
|
||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 539; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.242.160 (0.007 с.) |


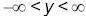 Ясно, що (0,0) є точкою глобального мінімуму функції f 0 (x) на множині X.
Ясно, що (0,0) є точкою глобального мінімуму функції f 0 (x) на множині X. (8.6)
(8.6)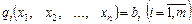 , (8.7)
, (8.7) і
і  мають бути диференційовними.
мають бути диференційовними.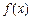 за умов виконання обмежень
за умов виконання обмежень  .
. (8.8)
(8.8) — деякі невідомі величини, що називаються множниками Лагранжа.
— деякі невідомі величини, що називаються множниками Лагранжа.
 (8.9)
(8.9) і
і 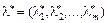 — стаціонарні точки. Оскільки, ці розв’язки отримані з необхідної умови екстремуму, то вони визначають максимум, мінімум задачі (8.6), (8.7) або можуть бути точками перегину (сідловими точками).
— стаціонарні точки. Оскільки, ці розв’язки отримані з необхідної умови екстремуму, то вони визначають максимум, мінімум задачі (8.6), (8.7) або можуть бути точками перегину (сідловими точками). існують другі частинні похідні і вони неперервні).
існують другі частинні похідні і вони неперервні). :
:
 , що складається з нульових елементів,
, що складається з нульових елементів, , елементи якої визначаються так:
, елементи якої визначаються так: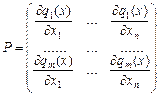 ,
,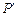 — транспонована матриця до Р розмірністю
— транспонована матриця до Р розмірністю  ,
,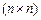 виду:
виду: , де
, де  .
.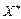 є точкою максимуму, якщо, починаючи з головного мінору порядку (m + 1), наступні (n – m) головних мінорів матриці Н утворюють знакозмінний числовий ряд, знак першого члена якого визначається множником
є точкою максимуму, якщо, починаючи з головного мінору порядку (m + 1), наступні (n – m) головних мінорів матриці Н утворюють знакозмінний числовий ряд, знак першого члена якого визначається множником  .
. .
.





