
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Властивості допоміжної задачі.Содержание книги
Поиск на нашем сайте
Справді, за умови yi ≥ 0 (i = 1, 2, …, m) завжди g ≥ 0. Отже, цільова функція цієї задачі обмежена знизу, а тому існує оптимальний розв’язок для задачі мінімізації.
Це твердження є очевидним. Отже, приймаючи α за початковий опорний розв’язок, можна розв’язати задачу (4) симплекс – методом. Нехай β = ( 3. Якщо Справді, за цієї умови γ, по - перше, є розв’язком задачі (3). По – друге, всі основні змінні допоміжної задачі для β знаходяться серед xj (j = 1, 2, …, n) і отже є основними змінними для γ. Тому всі вільні змінні γ дорівнюють нулю, тобто цей розв’язок є опорним. 4. Якщо серед чисел Справді, за цієї умови оптимальне значення g > 0. Якщо ж існує бодай один допустимий розв’язок ( Таким чином, метод штучного базису дає змогу завжди або знайти початковий опорний розв’язок, або встановити її нерозв’язність. Розглянемо такий приклад. f = 3х1 + х2 (mах)
Ввівши нові змінні х3, х4, зведемо цю модель до канонічної: f = 3х1 + х2 (mах)
Її симплекс – таблиця виглядає так:
Розв’яжемо цю задачу, використовуючи метод штучного базису. Оскільки вектор умов змінної x4 уже виглядає належним чином, то можна обмежитись додатковою змінною у1: g = у1 (min) або g´ = – у1 (mах)
Запишемо її у електронну симплекс – таблицю:
Приведемо її до базису х4, у1: для цього додамо до четвертого рядка другий. Отже, виокремимо новий діапазон А6:G8, рядки 2 і 3 скопіюємо у рядки 6 і 7 відповідно, у чарунку Е8 задамо формулу =Е4 + Е2, а формули решти чарунок рядка 8 скопіюємо з неї. В результаті дістанемо:
Серед оцінок базису є додатні, тож згідно з ознакою оптимальності треба виконати крок симплекс – методу. 1) Вибираємо оцінку δ1 = 1, зафарбуємо її. 2), 3) Елементи у стовпці 2 додатні, отже треба застосувати умову допустимості:
5) Виконаємо жорданове перетворення з ведучим елементом у А7:
5) Маємо симплекс – таблицю з новим набором основних змінних х1, у1, новий опорний розв’язок (3; 0; 0; 0; 2), нове значення цільової функції g = 2. 6) Оскільки знову існує додатна оцінка δ2 = 0,5, то переходимо до другого кроку сиплекс – методу і починаємо його з перевірки умови допустимості. Ведучим обираємо рядок 11, звідси ведучий елемент В11; черговим жордановим перетворенням дістаємо:
Нарешті всі оцінки невід’ємні, отримуємо оптимальний розв’язок допоміжної задачі (0; 2; 0; 1), g = 1. Отже, оскільки у1 = 1 > 0, то початкова задача нерозв’язна. Точніше кажучи, множина допустимих розв’язків є пустою. Наприкінці розглянемо ще графічне розв’язання початкової задачі f = 3х1 + х2 (mах)
На рисунку 5 зображені прямі L1: х1 + 2х2 = 5 і L2: 2х1 + 3х2 = 6. Оскільки 0 + 2∙0 = 0 < 5, то множина Ω допустимих розв’язків цієї задачі повинна бути розміщена по інший бік від прямої L1, ніж початок координат О(0;0). Аналогічно множина Ω повинна бути розміщена по той самий бік від прямої L2, що і початок координат. Разом з тим Ω повинна міститись у першій чверті, оскільки х1 ≥ 0, х2 ≥ 0. Як видно з рисунку, ці умови одночасно не виконуються для жодної точки, що є зримим підтвердженням результатів, отриманих симплекс – методом.
L2
L1
О х1
Рисунок 5 Питання, тести
1. Дана задача. У господарстві є два вида кормів вартістю 20 та 30 гривен за одиницю корму відповідно. У першому кормі міститься 2 одиниці вітаміну А та 3 одиниці вітаміну В, у другому 5 одиниць А та 2 одиниці В. Раціон повинен містити не менш як 9 одиниць А та 8 одиниць В. Скласти найдешевший раціон, який задовольняє цим вимогам. Математична модель такої задачі це
А: f = 20хА + 30хВ (max) Б: f = 20хА + 30хВ (min)
В: f = 20хА + 30хВ (max) Г: f = 20хА + 30хВ (min)
2. Дана задача. Нехай з трьох пунктів відправлення Р1, Р2, Р3 треба перевезти однорідний вантаж до трьох пунктів призначення М1, М2, М3, в тому числі з пункту Р1 – 12 т, з пункту Р2 – 8 т, з пункту Р3 – 10 т. Вантаж повинен надійти за призначенням у пункт М1 – 6 т, пункт М2 – 9 т, пункт М3 – 15 т. Система обмежень такої задачі це А: В:
3. Дана задача. Для виготовлення продукції двох видів (А і Б) на заводі використовують сировину трьох типів (1, 2 и 3). Кількість одиниць сировини кожного типу, що витрачається на один виріб кожного виду, запаси сировини та прибуток від одиниці продукції кожного виду наведені у таблиці:
Математична модель такої задачі це А: f = 200 хА + 300 хБ (min) Б: f = 200 хА + 300 хБ (max)
В: f = 200 хА + 300 хБ (min) Г: f = 200 хА + 300 хБ (max)
4. Дана задача. Для виготовлення продукції використовують три вида сировини і чотири способи виробництва. Запаси сировини, її витрати на одиницю продукції та кількість виготовляємої продукції по кожному способу (за годину роботи) наведені у таблиці.
Треба знайти план виробництва, за яким буде отримана найбільша кількість продукції.
Математична модель такої задачі це
А: f = 18x1 + 30x2 + 40x3 (min) Б: f = 18x1 + 30x2 + 40x3 (max)
В: f = 12x1 + 7x2 + 18x3 + 10x4 (max) Г: f = x1 + 2x2 + 3x3 + 4x4 (max)
5. На рисунку зображені множина Ω допустимих розв’язків задачі максимізації лінійного програмування ОАВСД, лінія нульового рівня цільової функції цієї задачі L0, і її вектор нормалі N, L1, L2 ║ L0.
х1
Рисунок
Множина оптимальних розв’язків даної задачі це
6. На рисунку зображені множина Ω допустимих розв’язків задачі максимізації лінійного програмування АВСД, лінія нульового рівня цільової функції цієї задачі L0, і її вектор нормалі N, L1, L2 ║ L0.
Множина оптимальних розв’язків L2
В: точка В Г: не існує Д: відрізок ВС Ω
N
х1
Рисунок
7. На рисунку зображені множина Ω допустимих розв’язків задачі максимізації лінійного програмування ОАВС, лінія нульового рівня цільової функції цієї задачі L0 і її вектор нормалі N, L1 ║ L0.
Ω L2
L0 Рисунок
Множина оптимальних розв’язків даної задачі це
7. На рисунку зображені множина Ω допустимих розв’язків задачі максимізації лінійного програмування ВАСD, лінія нульового рівня цільової функції цієї задачі L0, і її вектор нормалі N, L1 ║ L0.
Ω L2
L0 C L1
О Рисунок
Множина оптимальних розв’язків даної задачі це
9. Канонічна форма даної задачі лінійного програмування f = 2х1 + 3х2 + х3 (min)
це А: f = 2х1 + 3х2 + х3 (min) Б: f = 2х1 + 3х6 – 3х7 + х3 (min)
В: f = 2х1 + 3х2 + х3 (min) Г: f = – 2х1 – 3х2 – х3 (max)
10. Канонічна форма даної задачі лінійного програмування f = 5x1 – 2х2 + 3х3 (max)
це А: f = 5x1 – 2х2 – 3х3 (max) Б: f = – 5x1 + 2х2 + 3х3 (min)
В: f = 5х1 – 3x3 – 2х4 + 2х5 (max) Г: f = 5x1 – 2х2 – 3х3 (max)
11. Задача лінійного програмування наведена у канонічній формі: А: f = 5x1 – 2х2 – 3х3 (max) Б: f = – 5x1 + 2х2 + 3х3 (min)
В: f = 2х1 + 3х6 – 3х7 + х3 (min) Г: f = 2х1 + 3х2 + х3 (min)
12. Знайти опорний розв’язок, до базису якого приведена дана симплекс – таблиця і значення цільової функції на цьому розв’язку.
Відповідь: х1 =___ х2 =___ х3 =___ х4 =___ х5 =___ х6 =___ х7 =___ f =___
13. Знайти опорний розв’язок, до базису якого приведена дана симплекс – таблиця і значення цільової функції на цьому розв’язку.
Відповідь: х1 =___ х2 =___ х3 =___ х4 =___ х5 =___ х6 =___ х7 =___ f =___
14. Знайти опорний розв’язок, до базису якого приведена дана симплекс – таблиця і значення цільової функції на цьому розв’язку.
Відповідь: х1 =___ х2 =___ х3 =___ х4 =___ х5 =___ х6 =___ х7 =___ f =___
15. Ведучий елемент наступного жорданова перетворення
знаходиться у чарунці А: В2 Б: D3 В: А4 Г: С2 16. Ведучий елемент наступного жорданова перетворення
знаходиться у чарунці А: А2 Б: Е2 В: С4 Г: не існує
17. Ведучий елемент наступного жорданова перетворення
знаходиться у чарунці А: А2 Б: В3 В: В4 Г: D3
18. Яку чарунку треба вибрати, щоб отримати опорний розв’язок транспортної задачі, заданої таблицею?
А: А2 Б: В1 В: С2 Г: D3
19. Розв’язок транспортної задачі, заданий у таблиці, є опорним:
А: Б:
В: Г:
20. Допустимий розв’язком задачі лінійного програмування у канонічній формі є оптимальним, якщо А: у нього існує невироджений базис Б: для нього виконуються умови допустимості В: всі його оцінки відмінні від нуля Г: всі його оцінки недодатні
А: всі його оцінки недодатні Б: серед оцінок існує додатна В: серед оцінок існує додатна, а решта елементів цього стовпця недодатні Г: всі його оцінки невід’ємні
А: серед модулів відношень вільних членів до відповідних елементів стовпця обираємо найменше Б: серед модулів відношень вільних членів до відповідних елементів стовпця обираємо найбільше В: серед відношень вільних членів до відповідних додатних елементів стовпця обираємо найменше Г: серед відношень вільних членів до відповідних додатних елементів стовпця обираємо найбільше
Завдання 1. Дана задача. Для виготовлення продукції двох видів (А і Б) на заводі використовують сировину трьох типів (1, 2 и 3). Кількість одиниць сировини кожного типу, що витрачається на один виріб кожного виду, запаси сировини та прибуток від одиниці продукції кожного виду наведені у таблиці: Розв’язати цю задачу графічним методом.
2. Дана задача. Для виготовлення продукції використовують три вида сировини і чотири способи виробництва. Запаси сировини, її витрати на одиницю продукції та кількість виготовляємої продукції по кожному способу (за годину роботи) наведені у таблиці.
Треба знайти план виробництва, за яким буде отримана найбільша кількість продукції. Розв’язати цю задачу симплекс – методом.
f = 200 х1 + 300 х2 (max)
використавши надбудову Excel “Пошук розв’язку”.
4. Розв’язати задачу лінійного програмування f = 20х1 + 30х2 (min)
використавши метод жорданових перетворень для пошуку початкового допустимого опорного розв’язку.
5. Розв’язати задачу лінійного програмування f = 3х1 + х2 (mах)
використавши метод штучного базису для пошуку початкового допустимого опорного розв’язку.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 338; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.156.35 (0.012 с.) |

 ;
;  ; …;
; …;  ;
; 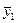 ;
; 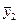 ; …;
; …; 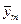 ) – це оптимальний розв’язок задачі (4).
) – це оптимальний розв’язок задачі (4).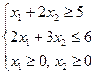 .
.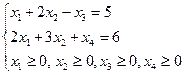 .
.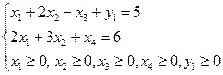 .
. х2
х2


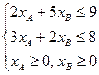

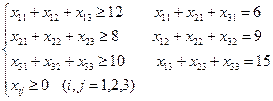
 Б:
Б: 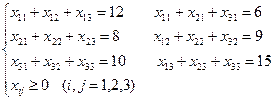
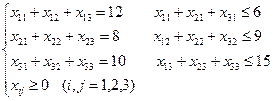 Г:
Г: 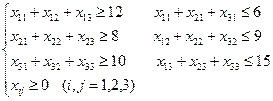

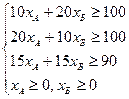
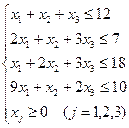

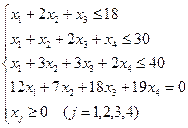

 х2
х2 L1 L2
L1 L2 А
А В
В Ω. С
Ω. С
 L0 N
L0 N О Д
О Д
 даної задачі це А
даної задачі це А А: точка А Б: точка Д L1
А: точка А Б: точка Д L1 В
В
 Д
Д L0 С
L0 С О
О х2
х2

 3 N(1;3)
3 N(1;3) A
A L1
L1 B
B
 O 1 C х1
O 1 C х1 х2
х2 B D
B D

 A N
A N х1
х1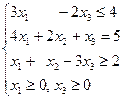


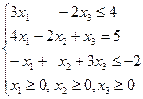
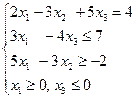
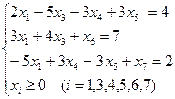
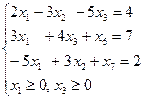
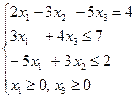

 ,
,


