
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод простої ітерації для СЛРСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Поширені методи розв’язування СЛР можна поділити на дві групи: точні й ітераційні. Точними називають такі методи, які дають змогу знайти точний розв’язок у припущенні, що всі обчислення проводяться без округлень, а коефіцієнти – точні числа. Тобто це такі методи обчислень, які не мають похибки методу. Прикладом точного методу є метод Гаусса, правило Крамера тощо. Ітераційними називають такі методи, які дають змогу знайти тільки наближений розв’язок системи із заздалегідь указаною точністю, хоч самі обчислення можуть проводитись і без округлень. Іншими словами, це методи, де крім похибок округлення треба враховувати також похибку метода. Проте, у реальних задачах не можливо обійтися без похибок округлення. Ці похибки в точних методах пропорційні кількості операцій, яка швидко зростає із зростанням кількості рівнянь і змінних. В ефективних ітераційних методах існує гранична обчислювальна похибка, яка майже не залежить від порядку рівняння. Крім того, ітераційні методи звичайно мають перевагу в ефективності, швидкості отримання наближеного розв’язку з указаною точністю. В ітераційних методах (або методах послідовних наближень) завжди формують послідовність хn наближень, де кожне наступне обчислюється з попередніх за певним (рекурентним) правилом; наближення хn збігаються до точного значення розв’язку. Але ж найчастіше в таких методах рівняння чи систему рівнянь F(x) = 0 замінюють еквівалентним х = Ф(х), де Ф(х) – деяка неперервна функція на множині W допустимих значень F. Далі обирають початкове наближення х0 Î W і послідовно обчислюють наступні наближення: хk = Ф(хk-1), k = 1,2,…. Якщо послідовність хk має границю х*, тобто Перехід від заданої СЛР Ах = b (А – матриця СЛР) до еквівалентної форми Ф(х) = 0 виконується практично так само, як і для рівняння в розділі. Покладемо С = Е – А, де Е – одинична матриця. Звідси b = Ах = (Е – (Е – А))х = (Е – С)х = х – Сх і отже х = Сх + b. Тут функція Ф(х) = Сх + b є неперервною на відповідному n – вимірному просторі L і визначає деякий ітераційний процес х = Ф(х). Для довільного початкового х0 Î L послідовність наближень хk = Ф(хk-1), k = 1,2,… буде збігатися до границі х*, якщо Ф(х) є стискуючим відображенням (за принцип стискуючих відображень Банаха: теорема 4 розділу). За означенням, Ф(х) є стискуючим, якщо для деякої норми ║ ║ на L і деякого числа q < 1 виконується нерівність ║Ф(х) – Ф(х')║ < q║x - x'║ при довільних х, х' Î L, звідки ║Ф(х) – Ф(х')║ = ║(Сх + b) – (Cx' + b)║ = ║Cx – Cx'║ = ║C(x – x')║ < q║x - x'║ (тобто якщо ║С║ < q). Тоді будуть виконуватись і всі наслідки принципу стискуючих відображень, у тому числі й оцінки похибок (теорема 6 розділу). Така норма ║ ║ та таке число q знайдуться завжди за умовою, що спектральний радіус С (тобто максимум модулів власних значень цієї матриці) не перевищує одиниці. Природним прикладом СЛР, де можна скористатися такою умовою є система Ах = b, для матриці системи A якої ô a iiô >
Якщо такі нерівності виконуються для СЛР Aх = b, то поділимо кожне рівняння цієї системи на a ii. Тоді для матриці А' отриманої еквівалентної системи А'х = b' діагональні елементи дорівнюють 1, для матриці С = Е – А' діагональні елементи дорівнюють нулю, а суми модулів недіагональних елементів Справді, нехай di = Задача 1. Розв’язати CЛР
Розв’язання. Оскільки 3,9 > 1,25 + 0,98, 3,45 > 0,74 + 0,84, 2,38 > 0,65 + 1,18, тобто виконана умова ô a iiô >
Поділимо кожний рядок цієї матриці на a ii:
В результаті отримаємо матрицю системи А' для СЛР А'х = b', еквівалентної даній.
Наступним кроком знайдемо матрицю С = Е – А'. Для цього спочатку помножимо А' на – 1
отримавши
а потім додамо одиничну матрицю: фактично ж задамо 0 замість – 1 у її діагональних елементах:
Тепер застосуємо ітераційний процес хk = Ф(хk-1), k = 1, 2, …, де Ф(х) = Сх + b'; за початкове наближення візьмемо b', яке знаходиться в діапазоні D5:D7: х0 = b'. Cпочатку розташуємо вектор b' у горизонтальному діапазоні А16:С16, тобто транспонуємо його за допомогою відповідного вбудованого оператора Excel. Для цього виділимо цей діапазон і задамо там оператор ТРАНСП(D5:D7). У наступному рядку задамо формули ітераційного процесу хk = Схk-1 + b': А17 = $А$16 + СУММПРОИЗВ($А$12:$С$12;А16:С16); В17 = $В$16 + СУММПРОИЗВ($А$13:$С$13;А16:С16); С17 = $С$16 + СУММПРОИЗВ($А$14:$С$14;А16:С16). У наступні рядки стовпців А, В, С ці формули треба копіювати (тобто протягувати). В результаті дістанемо:
У правильності отриманого розв’язку тут можна переконатись безпосередньою перевіркою:
звідки
Метод Зейделя Спочатку розглянемо метод Зейделя. Нехай задано СЛР Ах = b, де всі діагональні елементи відмінні від нуля. Якщо у m – вимірному просторі наближення хn = (хn1, хn2, …, хnm), то наступне наближення хn+1 = (хn+11, хn+12, …, хn+1m) визначається з такої системи рівнянь:
a21хn+11 + a22хn+12 + a23хn3 + … + a2mхnm = b2, (1) …………………………………………… am1хn+11 + am2хn+12 + am3хn+13 + … + ammхn+1m = bm.
Цю систему можна записати у вигляді Вхn+1 + Схn = b, де
a21 a22 0 … 0 0 0 a23 … a2m В = ………………., С = ……………….. am1 am2 am3 … amm 0 0 0 … 0
Звідси отримуємо хn+1 = – В-1Схn + В-1b. Отже, метод Зейделя є еквівалентним деякому методу простої ітерації. Звідси, зокрема, для його збіжності необхідно й достатньо, щоб всі власні значення матриці В-1С по модулю були менше 1. Оскільки ║– В-1С – λE║ = ║ В-1║×║C + λB║, то власні значення матриці В-1С є коренями рівняння ║C + λB║ = 0. Отже, необхідна й достатня умова збіжності методу Зейделя формулюється так: всі корені рівняння
a21λ a22λ a23 … a2m ……………………. = 0. am1λ am2λ am3λ … ammλ
Відзначимо також достатню умову збіжності методу Зейделя, аналогічну умові збіжності методу простої ітерації попереднього параграфу з аналогічним доведенням.
Теорема 1. Нехай для всіх і Задача розв’язання СЛР є модельною для більш складної задачі розв’язання систем нелінійних рівнянь і знаходження екстремуму функції багатьох змінних. Для перенесення методу Зейделя на ці більш складні задачі важливо зрозуміти найбільш загальні, якісні причини його збіжності, що можна здійснити за допомогою геометричної інтерпретації методу. Позначимо через Li площину
Рисунок 1. х1 Рисунок 2. х1
L2 L1
Рисунок 3.
Порівняння двох перших рисунків вказує на те, що збіжність методу Зейделя може змінитися при переміні місцями рівнянь системи. Цікава геометрична картина виникає у випадку, якщо матриця А симетрична, тобто (Ах, у) = (х, Ау) для довільних векторів х і у відповідної вимірності. Нехай А – дійсна, симетрична, додатне визначена матриця. Тоді метод Зейделя є еквівалентним задачі мінімізації функції F(y) = (A(y – x*), y – x*) – (Ax*, x*). Справді, для симетричної А маємо F(y) = (A(y – x*), y – x*) – (Ax*, x*) = (Ay, y) – 2(Ax*, y) = (Ay, y) – 2(b, y). Якщо А додатне визначена, то (A(y – x*), y – x*) > 0 за y ¹ x* і тому функція F(y) має мінімум, причому єдиний при y = x*. Отже, задача знаходження мінімуму функції F(y) рівносильна розв’язуванню рівняння Ах = b.
Рисунок 4. x1
Одним з методів мінімізації функції багатьох змінних є метод покоординатного спуску. Нехай маємо наближення (
Застосуємо метод покоординатного спуску для знаходження екстремуму функції F. Позначимо F(y) + (Ax*, x*) = (A(y – x*), y – x*) через F0(y). При мінімізації по змінній хk виконується зміщення по прямій, паралельній вісі хk до точки, де
Питання, тести
1. У які з m рівнянь CЛР треба підставити упорядковану сукупність n чисел, щоб довести, що вона є розв’язком цієї системи?
2. У CЛР
х1 – 2х2 + х3 = – 1 3х1 – х2 + 2х3 = 0
коефіцієнт а23 дорівнює
3. Елементарні операції над СЛР – це
4. СЛР може мати таку кількість розв’язків
5. В результаті кроку методу Гаусса отримаємо СЛР, у якій у порівнянні з СЛР, отриманій на попередньому кроці
6. Результатом методу Гаусса є зведення даної СЛР до рівносильної їй системи
А:
Б:
В:
Г:
Тоді перший крок алгоритму Гаусса реалізує така електронна таблиця: А:
Б:
В:
Г:
Тоді розв’язком даної СЛР є
Тоді це система трьох лінійних рівнянь з
Тоді останній крок алгоритму Гаусса реалізує така електронна таблиця: А:
Б:
В:
Г:
Тоді загальним розв’язком даної СЛР є
Тоді загальним розв’язком даної СЛР є
Скільки розв’язків має дана система?
Тоді для підрахунків матриці X = А:
Б:
В:
Г:
АЕ =
18. Задамо в електронній таблиці матрицю
Зведемо цю матрицю до діагональної форми методом Гаусса:
Тоді для матриць А =
19. Точними методами є
20. Ітераційними методами є
Тоді ітераційний процес хk = Схk-1 + b (k = 1, 2, …) визначається такими формулами А: А17 = $А$16 + СУММПРОИЗВ($А$12:$С$12;А16:С16); В17 = $В$16 + СУММПРОИЗВ($А$13:$С$13;А16:С16); С17 = $С$16 + СУММПРОИЗВ($А$14:$С$14;А16:С16). У наступні рядки стовпців А, В, С ці формули треба копіювати. Б: А17 = А16 + СУММПРОИЗВ($А$12:$С$12;А16:С16); В17 = В16 + СУММПРОИЗВ($А$13:$С$13;А16:С16); С17 = С16 + СУММПРОИЗВ($А$14:$С$14;А16:С16). У наступні рядки стовпців А, В, С ці формули треба копіювати. В: А17 = $А$16 + СУММПРОИЗВ($А$12:$С$12;А15:С15); В17 = $В$16 + СУММПРОИЗВ($А$13:$С$13;А15:С15); С17 = $С$16 + СУММПРОИЗВ($А$14:$С$14;А15:С15). У наступні рядки стовпців А, В, С ці формули треба копіювати. Г: А17 = $А$16 + СУММПРОИЗВ(А12:С12;А16:С16); В17 = $В$16 + СУММПРОИЗВ(А13:С13;А16:С16); С17 = $С$16 + СУММПРОИЗВ(А14:С14;А16:С16). У наступні рядки стовпців А, В, С ці формули треба копіювати.
Завдання
1. Розв’язати СЛР 2. Знайти матрицю X = 3. Знайти матрицю, обернену до матриці А = 4. Розв’язати СЛР 5. Розв’язати CЛР
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 609; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.228.61 (0.013 с.) |

 = х*, то ця границя буде розв’язком рівняння х = Ф(х). Справді, х* =
= х*, то ця границя буде розв’язком рівняння х = Ф(х). Справді, х* =  хk =
хk =  . Такі нерівності виконуються, наприклад, для матриць теорії інформації, де діагональні елементи a ii є ймовірністю правильного кодування повідомлення з номером i, а a ij з j ¹ i – ймовірності обрання альтернативних помилкових кодів.
. Такі нерівності виконуються, наприклад, для матриць теорії інформації, де діагональні елементи a ii є ймовірністю правильного кодування повідомлення з номером i, а a ij з j ¹ i – ймовірності обрання альтернативних помилкових кодів. < 1. Як і вище, СЛР А'х = b' еквівалентна рівності х = Ф(х) = Сх + b'. У якості норми в L візьмемо максимум модулів координат вектора: ║х║ = max ôxjô. Тоді для деякого числа q < 1 ║Сx║ < q║x║ при кожному х Î L, що означає: Ф – стискуюче відображення, а ітераційний процес хk = Ф(хk-1), k = 1, 2, … завжди буде збігатися при довільному х0 Î L.
< 1. Як і вище, СЛР А'х = b' еквівалентна рівності х = Ф(х) = Сх + b'. У якості норми в L візьмемо максимум модулів координат вектора: ║х║ = max ôxjô. Тоді для деякого числа q < 1 ║Сx║ < q║x║ при кожному х Î L, що означає: Ф – стискуюче відображення, а ітераційний процес хk = Ф(хk-1), k = 1, 2, … завжди буде збігатися при довільному х0 Î L. < 1, х = (х1, х2, …, хn) Î L. Тоді для вектора y = Cx маємо
< 1, х = (х1, х2, …, хn) Î L. Тоді для вектора y = Cx маємо  =
=  £
£  = di ×
= di ×  £ di ×
£ di ×  = di × ║x║. Остання нерівність випливає з того, що
= di × ║x║. Остання нерівність випливає з того, що  = 1, а опукла комбінація чисел ôxjô не перевищує
= 1, а опукла комбінація чисел ôxjô не перевищує  < 1, то отримуємо ║Cx║ = ║у║ =
< 1, то отримуємо ║Cx║ = ║у║ =  £ q ×║x║, що й потрібно.
£ q ×║x║, що й потрібно. методом простої ітерації.
методом простої ітерації. a11хn+11 + a12хn2 + a13хn3 + … + a1mхnm = b1,
a11хn+11 + a12хn2 + a13хn3 + … + a1mхnm = b1,

 a11 0 0 … 0 0 a12 a13 … a1m
a11 0 0 … 0 0 a12 a13 … a1m


 = bi. При отримані наближення (хn+11; хn+12; …; хn+1i-1; хn+1i; …; хn+1m) з наближення (хn+11; хn+12; …; хn+1i-1; хni; …; хn+1m) згідно з (1) наближення переміщується паралельно вісі хi до перетину з площиною Li. Отже, метод Зейделя геометрично складається з циклічних переміщень паралельно координатним осям хi до перетину з площинами Li. Наступні рисунки ілюструють при m = 2 випадки, коли метод Зейделя збігається, розбігається або має цикл.
= bi. При отримані наближення (хn+11; хn+12; …; хn+1i-1; хn+1i; …; хn+1m) з наближення (хn+11; хn+12; …; хn+1i-1; хni; …; хn+1m) згідно з (1) наближення переміщується паралельно вісі хi до перетину з площиною Li. Отже, метод Зейделя геометрично складається з циклічних переміщень паралельно координатним осям хi до перетину з площинами Li. Наступні рисунки ілюструють при m = 2 випадки, коли метод Зейделя збігається, розбігається або має цикл.
 х2 х1
х2 х1


 L1
L1





 L2 L1
L2 L1

 х2
х2
 х1
х1  x2
x2

 x0
x0

 ,
,  , …,
, …,  ) до точки екстремуму функції F(х1, х2, …, хm). Розглянемо функцію F(х1,
) до точки екстремуму функції F(х1, х2, …, хm). Розглянемо функцію F(х1,  її мінімуму. Потім, виходячи з наближення (
її мінімуму. Потім, виходячи з наближення ( , …,
, …, 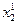 ,
,  = 0. Нове значення хk визначається з рівняння
= 0. Нове значення хk визначається з рівняння  2х1 – 3х2 + 4х3 = 2
2х1 – 3х2 + 4х3 = 2
 . Матриця цієї системи – це
. Матриця цієї системи – це 









 ,
,  і
і  у діапазонах А2:С3, А5:С6, А8:С9 відповідно так, як указано в наступній таблиці
у діапазонах А2:С3, А5:С6, А8:С9 відповідно так, як указано в наступній таблиці у діапазоні А11:С12 можна використати таку таблицю:
у діапазоні А11:С12 можна використати таку таблицю: , АЕ – 3 ´ 6 матриця,
, АЕ – 3 ´ 6 матриця,  . Зведемо матрицю АЕ до діагональної форми методом Гаусса: вона дістане вигляд ЕВ =
. Зведемо матрицю АЕ до діагональної форми методом Гаусса: вона дістане вигляд ЕВ =  , де В – деяка 3 ´ 3 матриця. Нехай Е – діагональна 3 ´ 3 матриця, Е =
, де В – деяка 3 ´ 3 матриця. Нехай Е – діагональна 3 ´ 3 матриця, Е =  . Тоді
. Тоді у діапазоні А1:С3 і В у діапазоні D13:F15
у діапазоні А1:С3 і В у діапазоні D13:F15
 методом Гаусса.
методом Гаусса. ×
×  – 5 ×
– 5 ×  , використавши вбудовані оператори Excel.
, використавши вбудовані оператори Excel. методом Гаусса.
методом Гаусса.


