
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Інші приклади ітераційних методів.Содержание книги
Поиск на нашем сайте
Все це зовсім не означає, що метод Ньютона безумовно краще, ніж метод лінійного інтерполювання або метод ітерації із сталим λ; насправді кожен має свої переваги. Так, наприклад, у методі Ньютона на відміну від інших методів на кожній ітерації треба обчислювати значення похідної, що може виявитись значно складнішим від обчислення функції. Якщо похідна мало змінюється на відрізку ізоляції, то можна спробувати замість значень f ′ (xk) в ітераціях xk скористатись значенням f ′ (x0) похідної у точці x0, тобто xk+1 = xk – У всіх цих методах збіг до кореня монотонний і з того боку від нього, де f (х) ∙ f ′′(х) > 0. А ітерації методу хорд збігаються з протилежного боку (див. попередній розділ). Тому іноді корисно об’єднати обидва методи і наближатися до кореня рівняння з двох боків, дістаючи наближення з недостачею і надлишком одночасно. За початкове наближення в методі хорд вибирають точку
y
f ′′(x) > 0
0
Рисунок 1.
На відрізку bk+1 = bk – Порівнюючи цю формулу для а k+1 з формулою класичного метода хорд, бачимо тільки одну різницю: на місці нерухомої точки с тут точка bk+1, яка збігається до кореня із швидкістю метода Ньютона. Отже швидкість цього метода повинна бути принаймні не меншою швидкості метода Ньютона. Перевіримо це безпосередньо на прикладі. Для застосування цього метода необхідно забезпечити наступні передумови. 1. Треба знайти відрізок ізоляції шуканого кореня. 2. Треба забезпечити, щоби на відрізку ізоляції не змінювався знак у f′′ (х), зменшуючи при необхідності початковий відрізок. 3. За початкове наближення а можна брати будь – яку точку відрізку ізоляції, у якій виконується умова f (а) ∙ f′′ (а) < 0. 4. За початкове наближення b можна взяти будь – яку точку відрізку ізоляції, у якій виконується умова f (b) ∙ f′′ (b) > 0. Розглянемо застосування методу на попередньому прикладі: розв‘язати рівняння f (x) = 2х + 5x – 3 = 0 з точністю e = 0,5*10-5. 1. Відрізок ізоляції для єдиного кореня цього рівняння [a;b] = [0;1]. 2. f′′ (х) > 0 при всіх х. 3,4. Оскільки f (0) = –2, f (1) = 4, то за початкові наближення можна взяти а = 0, b = 1. Нарешті знайдемо корінь з точністю e = 0.5*10-5 комбінованим методом за допомогою Excel. Надамо чарункам електронної таблиці таких значень:
Тут стовбці C, D і E ідентичні відповідним стовбцям електронної таблиці для метода Ньютона: С1 містить початкову точку b = 1, D1 значення f (b), Е1 значення f ′ (b), С2 формулу метода Ньютона. Разом з тим стовбці А, В, С і D містять інформацію, майже ідентичну відповідним стовбцям електронної таблиці методу лінійного інтерполювання: відмінність лише в тому, що у стовбцях С і D тепер змінні значення, отримані методом Ньютона. А саме у чарунку А1 початкова точка а = 0, у В1 значення f (а), у А2 формула метода хорд, де місце нерухомої точки зайняли значення з рядка 2 метода Ньютона: тобто спочатку працює цей метод, а далі його результати використовує метод хорд. В результаті отримуємо:
Тут додатково введений ще стовбець F, де підраховується різниця між значеннями у стовбцях С і А, тобто різниця εk між наближенням з надлишком, яке дає метод Ньютона, і наближенням з недостачею, яке забезпечує метод лінійного інтерполювання. Із цих даних безпосередньо видно, що збіжність методу квадратична: εk+1 ≈ εk2, тобто кількість значущих цифр наближення подвоюється з кожним кроком. Уже у рядку 4 (скоріше навіть класичного метода Ньютона) значення у стовбцях С і А не відрізняються з максимально можливим у комп’ютері числі значущих цифр. Тому подальші обчислення величини a k у стовбці А по формулі (6) призводять до повідомлення про помилку #ДЕЛ/0! (ділення на 0): надалі величина f (bk+1) – f (a k) у знаменнику цієї формули уже не відрізняється від нуля. Всі розглянуті вище методи вимагали передумовою попереднє відокремлення коренів. Нарешті розглянемо метод, який дозволяє розв’язувати рівняння f (х) = 0 на відрізку у
а а1 х1* а2 х2* х3* а3 b Рисунок 2.
З рисунку видно, що до першого кореня х1* збігається будь – який процес xk+1 = φ(xk), що починається в його околі між а та другим коренем х2*, наприклад, у точках а1 або а2. Тобто х1* – стійка нерухома точка процесу, так само і третій корінь х3*. Другий корінь х2* – нестійка нерухома точка, до неї не збігається жоден процес окрім того, що починається безпосередньо в точці х2*. Легко зрозуміти, що у загальному випадку стійкі та нестійкі нерухомі точки чергуються: за стійкою нестійка і навпаки. Якщо змінити знак λ, тобто розглянути процеси xk+1 = φ1(xk), де φ1(х) = х + λ∙ f (x), то стійкі нерухомі точки перетворяться на нестійкі і навпаки. Отже або процес xk+1 = φ(xk), або xk+1 = φ1(xk) збігається до кожного кореня f (x) на Можна впевнено стверджувати, що побудова, модифікація та реалізація алгоритмів, аналіз їх ефективності – це найкращий шлях вивчення обчислювальних методів.
Питання, тести
1. Відрізок [a;b] є відрізком ізоляції кореня рівняння
2. Нехай графік функції
3. Нехай графік функції А:
Б:
В:
Г:
4. Нехай на інтервалі (a;b) графік функції
5. Нехай на інтервалі (0;1) графік функції А:
Б:
В:
Г:
6. В наступній таблиці у стовпці А значення аргументу, у стовпці В відповідні значення функції
7. В наступній таблиці у стовпці А значення аргументу, у стовпці В відповідні значення функції
8. За таким варіантом наступного рисунку ітераційний процес х = φ(х) з початковою точкою А0 (х0, φ(х0)) збігається:
в г
10. Нехай │φ′(х)│< 1 на відрізку [a; b], φ(х*) = х* для деякого х* Î [a; b]. Тоді
11. Для ефективних ітераційних методів (тобто з малою константою Ліпшиця q) після деякої кількості кроків
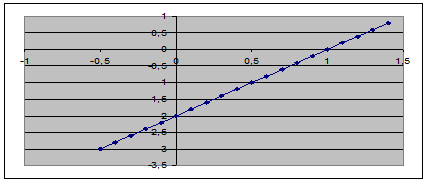
13. Нехай рівняння f (x) = 0 має корінь на відрізку його ізоляції [-1;-0,6], │ f ′(-1)│≈ 3,08 │ f ′(-0,6)│≈ 2,85; графік похідної f ′(x) наведений далі.
Тоді збіг ітераційного процесу хn+1 = φ(хn), де φ(х) = х – λ f (x) до кореня рівняння f (x) = 0 буде найшвидшим, якщо λ =
14. Рівняння f (x) = 2sin x – x2 + 2 = 0 має корінь на відрізку його ізоляції [1,8; 2,2], │ f ′(1,8)│≈ 4,05; │ f ′(2,2)│≈ 5,57; графік похідної f ′(x) наведений далі.
Тоді наступна таблиця визначає ітераційний процес хn+1 = φ(хn), де φ(х) = х – λ f (x), збіг якого до кореня рівняння f (x) = 0 буде найшвидшим:
А:
Б:
В:
Г:
15. Нехай хn+1 = φ(хn) – ітераційний процес, де φ(х) = х – λ f (x). Тоді за методом Ньютона λ =
16. [0; 1] є відрізком ізоляції кореня рівняння f (x) = 2х + 5x – 3 = 0. На цьому відрізку
17. [0;1] є відрізком ізоляції кореня рівняння f (x) = 2х + 5x – 3 = 0. Наступна таблиця визначає ітераційний процес пошуку кореня рівняння f (x) = 0 методом Ньютона:
А:
Б:
В:
Г:
18. Збіг ітераційного процесу хk = φ(хk-1) тим швидший, чим порядок його збіжності
19. Порядок збіжності ітераційного процесу α дорівнює
20. [0; 1] є відрізком ізоляції кореня рівняння f (x) = 2х + 5x – 3 = 0. На цьому відрізку
21. [0;1] є відрізком ізоляції кореня рівняння f (x) = 2х + 5x – 3 = 0. Наступна таблиця визначає ітераційний процес пошуку кореня рівняння f (x) = 0 методом хорд: А:
Б:
В:
Г:
Завдання 1. Відокремити корені рівняння 2соs x – x2 + 2 = 0 графічним методом. 2. Відокремити корені рівняння f (x) = sinx – x + 1 = 0 аналітичним методом. 3. Відокремити корені рівняння x2 – 3 соs x – 2 комбінованим методом. 4. Розв‘язати рівняння f (x) = 3х + 6x – 3 = 0 з точністю e = 0.5*10-5 методом дихотомії. 5. Методом простої ітерації розв‘язати рівняння f (x) = 3 ∙ sin x – x2 + 2 = 0 з точністю e = 0,5*10-5. 6. Методом Ньютона розв‘язати рівняння f (x) = 5х + 5x – 5 = 0 з точністю e = 0,5*10-5. 7. Методом хорд розв‘язати рівняння f (x) = 3х + 6x – 3 = 0 з точністю e = 0,5*10-5.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 710; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.33 (0.009 с.) |

 (k = 0,1,2,…). Ця формула визначає спрощений метод Ньютона. Очевидно, це метод ітерації із сталим λ =
(k = 0,1,2,…). Ця формула визначає спрощений метод Ньютона. Очевидно, це метод ітерації із сталим λ =  , а тому із лінійною збіжністю. Більш поширений метод полягає у тому, щоби похідну замінити її наближеним значенням:
, а тому із лінійною збіжністю. Більш поширений метод полягає у тому, щоби похідну замінити її наближеним значенням:  . Підставивши це наближення у формулу методу Ньютона, отримуємо xk+1 = xk –
. Підставивши це наближення у формулу методу Ньютона, отримуємо xk+1 = xk –  . Метод, що визначається такою формулою, називають методом січних. Річ у тому, що наближення xk+1 дістають як абсцису точки перетину осі Ох і січної, що проходить через точки (xk-1; f (xk-1)) та (xk; f (xk)), тобто з рівняння
. Метод, що визначається такою формулою, називають методом січних. Річ у тому, що наближення xk+1 дістають як абсцису точки перетину осі Ох і січної, що проходить через точки (xk-1; f (xk-1)) та (xk; f (xk)), тобто з рівняння  =
=  , де покладаємо у = 0.
, де покладаємо у = 0. де f (а) ∙ f ′′(а) < 0, а в методі Ньютона – точку
де f (а) ∙ f ′′(а) < 0, а в методі Ньютона – точку  , де f (b) ∙ f ′′(b) > 0.
, де f (b) ∙ f ′′(b) > 0.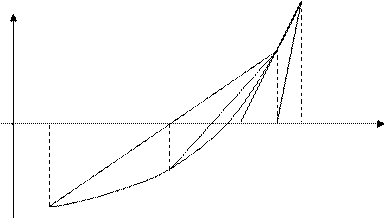
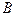










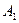

 застосовують спочатку метод дотичних, а потім – хорд. У результаті дістають нові наближення
застосовують спочатку метод дотичних, а потім – хорд. У результаті дістають нові наближення 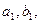 і початковий відрізок ізоляції кореня звузився. Для знаходження нових наближень застосовують метод дотичних і хорд уже на відрізку
і початковий відрізок ізоляції кореня звузився. Для знаходження нових наближень застосовують метод дотичних і хорд уже на відрізку  Такий процес продовжують доти, поки довжина відрізка
Такий процес продовжують доти, поки довжина відрізка 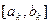 стане меншою величини
стане меншою величини  де
де  – наперед задана точність кореня. Формули цього комбінованого методу Ньютона та лінійного інтерполювання мають виглядати так:
– наперед задана точність кореня. Формули цього комбінованого методу Ньютона та лінійного інтерполювання мають виглядати так: , а k+1 = a k –
, а k+1 = a k –  (k = 0,1,2,…). (6)
(k = 0,1,2,…). (6) . З таким λ ітераційний процес xk+1 = φ(xk) при будь – якому початковому x0 є
. З таким λ ітераційний процес xk+1 = φ(xk) при будь – якому початковому x0 є  = х*. Звідси φ(х*) = х*, тобто f (x*) = 0. Справді, φ(х*) = φ(
= х*. Звідси φ(х*) = х*, тобто f (x*) = 0. Справді, φ(х*) = φ( хk) =
хk) =  х
х , якщо
, якщо перетинає вісь абсцис на (a;b)
перетинає вісь абсцис на (a;b)
 перетинає вісь абсцис на (a;b)
перетинає вісь абсцис на (a;b)



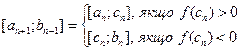




 . При цьому
. При цьому  < 0
< 0






