

Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
|
Подвійний перерахунок для методів Рунге – Кутта
Нехай задані послідовність х0, х1, …, хn рівновіддалених точок: хk = х0 + kh з кроком інтегрування диференціального рівняння h і послідовність  , ,  , …, , …,  з кроком h/2 так, щоби з кроком h/2 так, щоби  = хk (k = 0, 1, …, n). Розглянемо задачу Коші (1) у´ = f (x, y); у(х0) = у( = хk (k = 0, 1, …, n). Розглянемо задачу Коші (1) у´ = f (x, y); у(х0) = у( ) = у0, її чисельні розв’язки у0, у1, …, уn з кроком h і ) = у0, її чисельні розв’язки у0, у1, …, уn з кроком h і 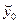 , ,  , …, , …,  з кроком h/2, отримані деяким методом Рунге – Кутта порядку точності s. Нехай εk = уk – у(хk) і з кроком h/2, отримані деяким методом Рунге – Кутта порядку точності s. Нехай εk = уk – у(хk) і  = =  – у(хk) відповідні похибки наближених значень уk та – у(хk) відповідні похибки наближених значень уk та  у деякій точці хk = у деякій точці хk =  . .
Метод подвійного перерахунку для методів Рунге – Кутта є узагальненням такого методу для інтегрування функцій і теж ґрунтується на двох аналогічних формулах.
1. ε = –  ≈ ≈  (правило Рунге) (6) (правило Рунге) (6)
2. у(хk) ≈  + ε = + ε =  + +  (аналог формули екстраполяції за Річардсоном). (7) (аналог формули екстраполяції за Річардсоном). (7)
Практичне застосування цих формул розглянемо в наступному параграфі. Тут далі наведені обґрунтування цих формул і, як результат, їх точне формулювання.
На кожному з відрізків [хk; хk+1] (k = 0, 1, …, n) завдовжки h розглянемо задачу Коші (1) у´ = f (x, y); у(хk) = уk і заданим методом Рунге – Кутта дістанемо наближене значення розв’язку у(хk + h) в точці хk+1, яке за умовою дорівнює уk+1 та похибку методу на кроці φk(h) = уk+1 – у(хk + h) =  hs+1 (0 < θk < 1) згідно з (4). Зокрема, на першому кроці φ0(h) = у1 – у(х0 + h) = hs+1 (0 < θk < 1) згідно з (4). Зокрема, на першому кроці φ0(h) = у1 – у(х0 + h) =  hs+1 (0 < θ0 < 1), на другому φ1(h) = у2 – у(х1 + h) = hs+1 (0 < θ0 < 1), на другому φ1(h) = у2 – у(х1 + h) =  hs+1 (0 < θ1 < 1). Як було зазначено та й видно безпосередньо, величина похибки методу Рунге – Кутта порядку точності s на кроці має порядок s + 1: φk(h) = О(hs+1). Розглянемо перетворення Tmk(z) (m < k), яке кожній початковій умові z для задачі Коші у´ = f (x, y); у(хm) = z ставить у відповідність значення розв’язку в точці хk: у(хk) = Tmk(z). Тоді під дією диференціального рівняння відрізок [у1; у(х0 + h)] між точним та наближеним значенням, отриманими на кроці 1, за другий крок пересунеться в [T12(у1); T12(у(х0 + h)) ]. Довжина цього відрізку ôT12(у1) – T12(у(х0 + h))ô = А12ôу1 – у(х0 + h)ô = А12ôφ0(h)ô, де А12 > 0 – стала. Оскільки ôT12(у1) – T12(у(х0 + h))ô = ô hs+1 (0 < θ1 < 1). Як було зазначено та й видно безпосередньо, величина похибки методу Рунге – Кутта порядку точності s на кроці має порядок s + 1: φk(h) = О(hs+1). Розглянемо перетворення Tmk(z) (m < k), яке кожній початковій умові z для задачі Коші у´ = f (x, y); у(хm) = z ставить у відповідність значення розв’язку в точці хk: у(хk) = Tmk(z). Тоді під дією диференціального рівняння відрізок [у1; у(х0 + h)] між точним та наближеним значенням, отриманими на кроці 1, за другий крок пересунеться в [T12(у1); T12(у(х0 + h)) ]. Довжина цього відрізку ôT12(у1) – T12(у(х0 + h))ô = А12ôу1 – у(х0 + h)ô = А12ôφ0(h)ô, де А12 > 0 – стала. Оскільки ôT12(у1) – T12(у(х0 + h))ô = ô  ô = ôT´12(ζ)ô∙ôу1 – у(х0 + h)ô = ôT´12(ζ)ô∙ôφ0(h)ô, то А12 = ôT´12(ζ)ô, де ζ Î [у1; у(х0 + h)]. Сумарна похибка на другому кроці ε2 = у2 – у(х2) дорівнює сумі похибки на цьому кроці φ1(h) і похибки на першому кроці φ0(h), перетвореній за другий крок диференціальним рівнянням, тобто перетворенням T12: ε2 = у2 – у(х2) = φ1(h) + А12 φ0(h). На третьому кроці сумарна похибка дорівнює сумі похибки на цьому кроці φ2(h), похибки на другому кроці φ1(h), перетвореній за третій крок диференціальним рівнянням, тобто перетворенням T23 та похибки на першому кроці φ0(h), перетвореній за другий та третій кроки дією T13: ε3 = у3 – у(х3) = φ2(h) + А23 φ1(h) + А13 φ0(h), де А13 = ôT´13(ζ13)ô, ζ13 Î [у1; у(х0 + h)], А23 = ôT´23(ζ)ô, ζ Î [у2; у(х1 + h)]. У загальному випадку сумарна похибка на кроці k ô = ôT´12(ζ)ô∙ôу1 – у(х0 + h)ô = ôT´12(ζ)ô∙ôφ0(h)ô, то А12 = ôT´12(ζ)ô, де ζ Î [у1; у(х0 + h)]. Сумарна похибка на другому кроці ε2 = у2 – у(х2) дорівнює сумі похибки на цьому кроці φ1(h) і похибки на першому кроці φ0(h), перетвореній за другий крок диференціальним рівнянням, тобто перетворенням T12: ε2 = у2 – у(х2) = φ1(h) + А12 φ0(h). На третьому кроці сумарна похибка дорівнює сумі похибки на цьому кроці φ2(h), похибки на другому кроці φ1(h), перетвореній за третій крок диференціальним рівнянням, тобто перетворенням T23 та похибки на першому кроці φ0(h), перетвореній за другий та третій кроки дією T13: ε3 = у3 – у(х3) = φ2(h) + А23 φ1(h) + А13 φ0(h), де А13 = ôT´13(ζ13)ô, ζ13 Î [у1; у(х0 + h)], А23 = ôT´23(ζ)ô, ζ Î [у2; у(х1 + h)]. У загальному випадку сумарна похибка на кроці k
εk = уk – у(хk) = φk-1(h) + Аk-1k φk-2(h) + Аk-2k φk-3(h) + … + А1k φ0(h) =  , ,
де Аkk = 1, а для i < k Аik = ôT´ik(ζik)ô, де ζik Î [уi; у(хi-1 + h)].
На кожному відрізку [хk; хk+1] розташовані два відрізка: [  ; ; 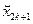 ] та [ ] та [ 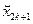 ; ;  ] (бо хk = ] (бо хk =  , хk+1 = , хk+1 =  ). Аналогічно попередньому на кожному з цих відрізків завдовжки h/2 розглянемо задачу Коші (1) у´ = f (x, y); у( ). Аналогічно попередньому на кожному з цих відрізків завдовжки h/2 розглянемо задачу Коші (1) у´ = f (x, y); у( ) = ) =  і у´ = f (x, y); у( і у´ = f (x, y); у(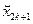 ) = ) = 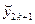 . Даним методом Рунге – Кутта дістанемо наближене значення розв’язку у( . Даним методом Рунге – Кутта дістанемо наближене значення розв’язку у( + h/2) у точці + h/2) у точці 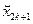 , яке за побудовою дорівнює , яке за побудовою дорівнює 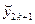 та наближене значення розв’язку у( та наближене значення розв’язку у(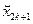 + h/2) у точці + h/2) у точці 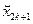 , яке дорівнює , яке дорівнює  . Дістанемо також похибки методу на кроці . Дістанемо також похибки методу на кроці  = = 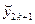 – у( – у( + h/2) = + h/2) =  (h/2)s+1 (0 < θ2k < 1/2) і (h/2)s+1 (0 < θ2k < 1/2) і  = =  – у( – у(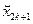 + h/2) = + h/2) =  (h/2)s+1 (0<θ2k+1<1/2), які мають порядок s + 1. Розглянемо також перетворення (h/2)s+1 (0<θ2k+1<1/2), які мають порядок s + 1. Розглянемо також перетворення  (m < k), яке кожній початковій умові z для задачі Коші у´ = f (x, y); у( (m < k), яке кожній початковій умові z для задачі Коші у´ = f (x, y); у( ) = z ставить у відповідність значення розв’язку в точці ) = z ставить у відповідність значення розв’язку в точці  : у( : у( ) = ) =  . Тоді . Тоді  – сумарна похибка на кроці 2k – це, як і вище, – сумарна похибка на кроці 2k – це, як і вище,  = =  – у(хk) = – у(хk) =  = =
=  + +   + +   + … + + … +  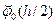 , ,
де  = 1, а для i < k = 1, а для i < k  = ô = ô  ô, ô,  Î [ Î [  ; y( ; y( + h/2)]. Отже, одночасно + h/2)]. Отже, одночасно
у(хk) = уk – εk = уk –  (8) (8)
у(хk) =  – –  = =  – –  . (9) . (9)
На відрізку [хi; хi+1] розташовані два відрізка [  ; ;  ] та [ ] та [  ; ;  ], (хi = ], (хi =  , хi+1 = , хi+1 =  ), тож доданку Аikφi-1(h) = Аik ), тож доданку Аikφi-1(h) = Аik  hs+1 (0 < θi-1 < 1) у (8) відповідають два доданки у (9): hs+1 (0 < θi-1 < 1) у (8) відповідають два доданки у (9):   = =   (h/2)s+1 (0 < θ2i-1 < 1/2) і (h/2)s+1 (0 < θ2i-1 < 1/2) і 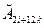  = = 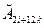 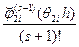 (h/2)s+1 (0 < θ2i < 1/2). Тут Аik = ôT´ik(ζik)ô, де ζik Î [уi; у(хi-1+ h)], (h/2)s+1 (0 < θ2i < 1/2). Тут Аik = ôT´ik(ζik)ô, де ζik Î [уi; у(хi-1+ h)],  =ô =ô  ô, де ô, де 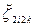 Î [ Î [  ;y( ;y( + h/2)], + h/2)], 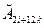 =ô =ô 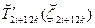 ô, де ô, де  Î [ Î [  ; y( ; y( + h/2)] відрізняються між собою величиною порядку h згідно з теоремою Лагранжа, оскільки за означенням Tik = + h/2)] відрізняються між собою величиною порядку h згідно з теоремою Лагранжа, оскільки за означенням Tik =  , а , а  відрізняється від відрізняється від  значеннями порядку h. Так само і величини значеннями порядку h. Так само і величини  , ,  і і  за означенням відрізняються між собою величиною порядку h згідно з теоремою Лагранжа. Тому спочатку знехтуємо відмінністю між величинами Аik за означенням відрізняються між собою величиною порядку h згідно з теоремою Лагранжа. Тому спочатку знехтуємо відмінністю між величинами Аik  , ,   , , 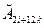  порядку h і покладемо Мi = Аik порядку h і покладемо Мi = Аik  ≈ ≈   ≈ ≈ 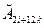 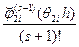 . Тоді (8) і (9) набувають вигляду . Тоді (8) і (9) набувають вигляду
у(хk) = уk – εk ≈ уk –  hs+1 = уk – Сhs (10) hs+1 = уk – Сhs (10)
у(хk) =  – –  ≈ ≈  – 2 – 2  (h/2)s+1 = (h/2)s+1 =  – С(h/2)s, (11) – С(h/2)s, (11)
де С =  h. (Якщо відрізок [х0, хk] вважати порядку одиниці, то k ~ h. (Якщо відрізок [х0, хk] вважати порядку одиниці, то k ~  , а отже і С = h , а отже і С = h  порядку одиниці). Відомими в (11) є уk, порядку одиниці). Відомими в (11) є уk,  , h і s, невідомими у(хk) та С. Отже, це система двох лінійних рівнянь з двома невідомими. Звідси , h і s, невідомими у(хk) та С. Отже, це система двох лінійних рівнянь з двома невідомими. Звідси  – С(h/2)s – (уk – Сhs) ≈ 0; – С(h/2)s – (уk – Сhs) ≈ 0;  – уk ≈ С( – уk ≈ С( )s – Сhs = С( )s – Сhs = С( )s(1 – 2s) = )s(1 – 2s) =  (1 – 2s), звідки знаходимо (6) (1 – 2s), звідки знаходимо (6)  ≈ – ≈ –  (правило Рунге). Тому (7): у(хk) ≈ (правило Рунге). Тому (7): у(хk) ≈  + +  (аналог формули екстраполяції за Річардсоном). Єдине неточне припущення, яке було зроблено в цьому доведенні – це рівність Аik (аналог формули екстраполяції за Річардсоном). Єдине неточне припущення, яке було зроблено в цьому доведенні – це рівність Аik  ≈ ≈   ≈ ≈ 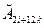 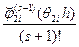 , насправді ці величини відрізняються між собою на величини порядку h. Тому різниці між величинами , насправді ці величини відрізняються між собою на величини порядку h. Тому різниці між величинами
Аikφi-1(h) = Аik  hs+1, hs+1,   = =   hs+1 і hs+1 і 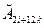  = = 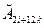 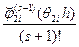 hs+1 – це величини порядку hs+2, а різниці між їх сумами по всім k = 0, 1, …, n – величини порядку hs+1. Врахування цих величин приводить до точного варіанту формул (6) і (7): hs+1 – це величини порядку hs+2, а різниці між їх сумами по всім k = 0, 1, …, n – величини порядку hs+1. Врахування цих величин приводить до точного варіанту формул (6) і (7):
1.  = – = –  + О(hs+1), 2. у(хk) = + О(hs+1), 2. у(хk) =  + +  + О(hs+1). (12) + О(hs+1). (12)
Отже,  = =  + +  – це наближення до точного розв’язку у(хk) порядку точності s + 1 у точці хk. Нехай ще дана послідовність рівновіддалених точок – це наближення до точного розв’язку у(хk) порядку точності s + 1 у точці хk. Нехай ще дана послідовність рівновіддалених точок  , ,  , …, , …,  з кроком інтегрування h/4 так, щоби з кроком інтегрування h/4 так, щоби  = хk (k = 0, 1, …, n). Розглянемо задачу Коші (1) у´ = f (x, y); у(х0) = у( = хk (k = 0, 1, …, n). Розглянемо задачу Коші (1) у´ = f (x, y); у(х0) = у( ) = у0, її чисельні розв’язки ) = у0, її чисельні розв’язки  , ,  , …, , …,  , отримані тим же методом Рунге – Кутта порядку точності s. Тоді метод подвійного перерахунку так само можна застосувати до цієї послідовності наближень і до попередньої , отримані тим же методом Рунге – Кутта порядку точності s. Тоді метод подвійного перерахунку так само можна застосувати до цієї послідовності наближень і до попередньої 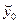 , ,  , …, , …,  з кроком h/2 у точках з кроком h/2 у точках  , ,  , …, , …,  ( ( = =  ). В результаті отримаємо оцінку похибки за правилом Рунге і уточнене значення за аналогом формули екстраполяції Річардсона: ). В результаті отримаємо оцінку похибки за правилом Рунге і уточнене значення за аналогом формули екстраполяції Річардсона:
1.  = – = –  + О(hs+1), 2. у(хk) = + О(hs+1), 2. у(хk) =  + +  + О(hs+1). (13) + О(hs+1). (13)
Тут 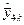 = =  – –  – це, як і – це, як і  , ще одне наближення порядку точності s + 1 до точного розв’язку у(хk) у точці хk. Тоді можна знову застосувати правило Рунге до цих двох уточнених наближень , ще одне наближення порядку точності s + 1 до точного розв’язку у(хk) у точці хk. Тоді можна знову застосувати правило Рунге до цих двох уточнених наближень 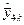 і і  : :  = – = –  + О(hs+2). Тобто + О(hs+2). Тобто  насправді виявиться похибкою порядку hs+1, а уточнене наближення насправді виявиться похибкою порядку hs+1, а уточнене наближення  = = 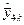 + +  буде мати порядок уже принаймні порядок точності s + 2. Процес можна продовжити і далі, отримуючи наближення порядку s + 3, s + 4, …. Доведення такого методу кратного перерахунку принципово таке ж, хоча вимагає значних технічних зусиль. Реалізацію цього метода за допомогою Excel розглянемо у наступному параграфі. буде мати порядок уже принаймні порядок точності s + 2. Процес можна продовжити і далі, отримуючи наближення порядку s + 3, s + 4, …. Доведення такого методу кратного перерахунку принципово таке ж, хоча вимагає значних технічних зусиль. Реалізацію цього метода за допомогою Excel розглянемо у наступному параграфі.
|



 ,
,  , …,
, …,  з кроком h/2 так, щоби
з кроком h/2 так, щоби  = хk (k = 0, 1, …, n). Розглянемо задачу Коші (1) у´ = f (x, y); у(х0) = у(
= хk (k = 0, 1, …, n). Розглянемо задачу Коші (1) у´ = f (x, y); у(х0) = у(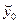 ,
,  , …,
, …,  з кроком h/2, отримані деяким методом Рунге – Кутта порядку точності s. Нехай εk = уk – у(хk) і
з кроком h/2, отримані деяким методом Рунге – Кутта порядку точності s. Нехай εk = уk – у(хk) і  =
=  – у(хk) відповідні похибки наближених значень уk та
– у(хk) відповідні похибки наближених значень уk та  (правило Рунге) (6)
(правило Рунге) (6) hs+1 (0 < θk < 1) згідно з (4). Зокрема, на першому кроці φ0(h) = у1 – у(х0 + h) =
hs+1 (0 < θk < 1) згідно з (4). Зокрема, на першому кроці φ0(h) = у1 – у(х0 + h) =  hs+1 (0 < θ0 < 1), на другому φ1(h) = у2 – у(х1 + h) =
hs+1 (0 < θ0 < 1), на другому φ1(h) = у2 – у(х1 + h) =  hs+1 (0 < θ1 < 1). Як було зазначено та й видно безпосередньо, величина похибки методу Рунге – Кутта порядку точності s на кроці має порядок s + 1: φk(h) = О(hs+1). Розглянемо перетворення Tmk(z) (m < k), яке кожній початковій умові z для задачі Коші у´ = f (x, y); у(хm) = z ставить у відповідність значення розв’язку в точці хk: у(хk) = Tmk(z). Тоді під дією диференціального рівняння відрізок [у1; у(х0 + h)] між точним та наближеним значенням, отриманими на кроці 1, за другий крок пересунеться в [T12(у1); T12(у(х0 + h)) ]. Довжина цього відрізку ôT12(у1) – T12(у(х0 + h))ô = А12ôу1 – у(х0 + h)ô = А12ôφ0(h)ô, де А12 > 0 – стала. Оскільки ôT12(у1) – T12(у(х0 + h))ô = ô
hs+1 (0 < θ1 < 1). Як було зазначено та й видно безпосередньо, величина похибки методу Рунге – Кутта порядку точності s на кроці має порядок s + 1: φk(h) = О(hs+1). Розглянемо перетворення Tmk(z) (m < k), яке кожній початковій умові z для задачі Коші у´ = f (x, y); у(хm) = z ставить у відповідність значення розв’язку в точці хk: у(хk) = Tmk(z). Тоді під дією диференціального рівняння відрізок [у1; у(х0 + h)] між точним та наближеним значенням, отриманими на кроці 1, за другий крок пересунеться в [T12(у1); T12(у(х0 + h)) ]. Довжина цього відрізку ôT12(у1) – T12(у(х0 + h))ô = А12ôу1 – у(х0 + h)ô = А12ôφ0(h)ô, де А12 > 0 – стала. Оскільки ôT12(у1) – T12(у(х0 + h))ô = ô  ô = ôT´12(ζ)ô∙ôу1 – у(х0 + h)ô = ôT´12(ζ)ô∙ôφ0(h)ô, то А12 = ôT´12(ζ)ô, де ζ Î [у1; у(х0 + h)]. Сумарна похибка на другому кроці ε2 = у2 – у(х2) дорівнює сумі похибки на цьому кроці φ1(h) і похибки на першому кроці φ0(h), перетвореній за другий крок диференціальним рівнянням, тобто перетворенням T12: ε2 = у2 – у(х2) = φ1(h) + А12 φ0(h). На третьому кроці сумарна похибка дорівнює сумі похибки на цьому кроці φ2(h), похибки на другому кроці φ1(h), перетвореній за третій крок диференціальним рівнянням, тобто перетворенням T23 та похибки на першому кроці φ0(h), перетвореній за другий та третій кроки дією T13: ε3 = у3 – у(х3) = φ2(h) + А23 φ1(h) + А13 φ0(h), де А13 = ôT´13(ζ13)ô, ζ13 Î [у1; у(х0 + h)], А23 = ôT´23(ζ)ô, ζ Î [у2; у(х1 + h)]. У загальному випадку сумарна похибка на кроці k
ô = ôT´12(ζ)ô∙ôу1 – у(х0 + h)ô = ôT´12(ζ)ô∙ôφ0(h)ô, то А12 = ôT´12(ζ)ô, де ζ Î [у1; у(х0 + h)]. Сумарна похибка на другому кроці ε2 = у2 – у(х2) дорівнює сумі похибки на цьому кроці φ1(h) і похибки на першому кроці φ0(h), перетвореній за другий крок диференціальним рівнянням, тобто перетворенням T12: ε2 = у2 – у(х2) = φ1(h) + А12 φ0(h). На третьому кроці сумарна похибка дорівнює сумі похибки на цьому кроці φ2(h), похибки на другому кроці φ1(h), перетвореній за третій крок диференціальним рівнянням, тобто перетворенням T23 та похибки на першому кроці φ0(h), перетвореній за другий та третій кроки дією T13: ε3 = у3 – у(х3) = φ2(h) + А23 φ1(h) + А13 φ0(h), де А13 = ôT´13(ζ13)ô, ζ13 Î [у1; у(х0 + h)], А23 = ôT´23(ζ)ô, ζ Î [у2; у(х1 + h)]. У загальному випадку сумарна похибка на кроці k ,
,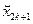 ] та [
] та [  ] (бо хk =
] (бо хk = 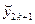 . Даним методом Рунге – Кутта дістанемо наближене значення розв’язку у(
. Даним методом Рунге – Кутта дістанемо наближене значення розв’язку у( . Дістанемо також похибки методу на кроці
. Дістанемо також похибки методу на кроці  =
=  (h/2)s+1 (0 < θ2k < 1/2) і
(h/2)s+1 (0 < θ2k < 1/2) і  =
=  (h/2)s+1 (0<θ2k+1<1/2), які мають порядок s + 1. Розглянемо також перетворення
(h/2)s+1 (0<θ2k+1<1/2), які мають порядок s + 1. Розглянемо також перетворення  (m < k), яке кожній початковій умові z для задачі Коші у´ = f (x, y); у(
(m < k), яке кожній початковій умові z для задачі Коші у´ = f (x, y); у( ) = z ставить у відповідність значення розв’язку в точці
) = z ставить у відповідність значення розв’язку в точці  : у(
: у( =
= +
+ 
 +
+ 
 + … +
+ … + 
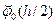 ,
, = 1, а для i < k
= 1, а для i < k  = ô
= ô  ô,
ô,  Î [
Î [  ; y(
; y( + h/2)]. Отже, одночасно
+ h/2)]. Отже, одночасно ;
;  ] та [
] та [  ], (хi =
], (хi =  hs+1 (0 < θi-1 < 1) у (8) відповідають два доданки у (9):
hs+1 (0 < θi-1 < 1) у (8) відповідають два доданки у (9): 
 =
=  (h/2)s+1 (0 < θ2i-1 < 1/2) і
(h/2)s+1 (0 < θ2i-1 < 1/2) і 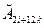
 =
= 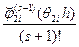 (h/2)s+1 (0 < θ2i < 1/2). Тут Аik = ôT´ik(ζik)ô, де ζik Î [уi; у(хi-1+ h)],
(h/2)s+1 (0 < θ2i < 1/2). Тут Аik = ôT´ik(ζik)ô, де ζik Î [уi; у(хi-1+ h)],  ô, де
ô, де 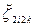 Î [
Î [  ;y(
;y( + h/2)],
+ h/2)], 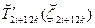 ô, де
ô, де  Î [
Î [  ; y(
; y( , а
, а  відрізняється від
відрізняється від  ,
,  і
і  за означенням відрізняються між собою величиною порядку h згідно з теоремою Лагранжа. Тому спочатку знехтуємо відмінністю між величинами Аik
за означенням відрізняються між собою величиною порядку h згідно з теоремою Лагранжа. Тому спочатку знехтуємо відмінністю між величинами Аik  hs+1 = уk – Сhs (10)
hs+1 = уk – Сhs (10) , а отже і С = h
, а отже і С = h  )s – Сhs = С(
)s – Сhs = С( =
=  =
=  =
=  ,
,  , …,
, …,  з кроком інтегрування h/4 так, щоби
з кроком інтегрування h/4 так, щоби  = хk (k = 0, 1, …, n). Розглянемо задачу Коші (1) у´ = f (x, y); у(х0) = у(
= хk (k = 0, 1, …, n). Розглянемо задачу Коші (1) у´ = f (x, y); у(х0) = у( ,
,  , …,
, …,  , отримані тим же методом Рунге – Кутта порядку точності s. Тоді метод подвійного перерахунку так само можна застосувати до цієї послідовності наближень і до попередньої
, отримані тим же методом Рунге – Кутта порядку точності s. Тоді метод подвійного перерахунку так само можна застосувати до цієї послідовності наближень і до попередньої  = –
= –  + О(hs+1), 2. у(хk) =
+ О(hs+1), 2. у(хk) =  +
+ 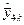 =
=  = –
= –  + О(hs+2). Тобто
+ О(hs+2). Тобто  =
= 


