
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод Ньютона. Порядок збіжності ітераційного процесу.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Розглянемо класичний ітераційний метод обчислення кореня х* рівняння f (x) = 0 на відрізку ізоляції [a;b], який є простим і дуже ефективним одночасно – метод Ньютона. Нехай хk – відоме k– е наближення кореня, треба знайти хk+1. Будемо вважати, що f (x) двічі диференційовна на [a;b] і застосуємо формулу Тейлора в околі точки хk: f (x) = f (хk) + f′ (хk)(х – хk) + ½ f′′ (хk)(х – хk)2 + … = 0. Нехтуючи нелінійними відносно х – хk додатками, отримаємо f (хk) + f′ (хk)(х – хk) = 0, звідки х = хk – хk+1 = хk – Ця формула і визначає ітераційний метод Ньютона: тут φ(х) = х – λ(х) ∙ f (x), λ(х) = Метод Ньютона має просту геометричну інтерпретацію. Рівняння y = f (хk) + f′ (хk)(х – хk) – це рівняння дотичної до графіку функції y = f (х) у точці хk, а отже вище знайдене хk+1 є точкою перетину цієї дотичної з віссю абсцис. Тому метод Ньютона називають ще методом дотичних. Будемо вважати, що не тільки f′ (х), але й f′′ (х) не змінює знак на [a;b], тобто що f′′ (х*) ≠ 0 і відрізок ізоляції обрано достатньо малим. Тож можливі чотири варіанти залежно від знаків f′ (х) та f′′ (х). Наприклад, якщо f′ (х) > 0, f′′ (х) < 0, то функція f (х) є зростаючою та опуклою, як це зображено на наступному рисунку 1. З нього можна
Рисунок 1.
Рисунок 2.
Рисунок 3.
Рисунок 4.
безпосередньо побачити, що для всіх можливих варіантів з одного боку відрізка ізоляції ітерації монотонно збігаються до кореня х*, а з другого можуть опинитись за межами відрізку вже на першому кроці. Легко переконатись (рисунки 1 – 4), що збіг спостерігається при всіх варіантах на тому боці, де виконується умова f (х) ∙ f′′ (х) > 0. Отже, для застосування метода Ньютона необхідно забезпечити наступні передумови. 1. Треба знайти відрізок ізоляції шуканого кореня. 2. Треба забезпечити, щоби на відрізку ізоляції не змінювався знак у f′′ (х), зменшуючи при необхідності початковий відрізок. 3. За початкове наближення можна брати будь – яку точку х відрізку ізоляції, у якій виконується умова f (х) ∙ f′′ (х) > 0. Розглянемо застосування методу Ньютона на прикладі задачі: розв‘язати рівняння f (x) = 2х + 5x – 3 = 0 з точністю e = 0,5*10-5. 1. Ця задача уже була розв’язана методом дихотомії і там був знайдений відрізок ізоляції [a;b] = [0;1] для єдиного кореня цього рівняння. 2. f′ (х) = 2х(ln 2) + 5, f′′ (х) = 2х(ln 2)2 > 0 при всіх х. Отже на [0;1] знак f′′ (х) не змінюється. 3. Як з графіку функції у = f (x), так і обраховуючи безпосередньо, отримаємо f (0) = –2, f (1) = 4. Тому за початкове наближення можна взяти точку b = 1. 4. Нарешті знайдемо корінь на [0;1] з точністю e = 0.5*10-5 методом Ньютона за допомогою Excel. Надамо чарункам електронної таблиці таких значень:
Тут у А1 початкова точка b = 1, у В1 значення f (x) при х = А1, у С1 – значення f′ (х) при х = А1, у А2 задано формулу метода Ньютона хk+1 = хk –
Тут стабілізація здійснилась за п’ять кроків при максимально можливому для комп’ютера числі значущих цифр у чарунку на відміну від методу дихотомії, де вона відбулась лише при 23 ітераціях, та й то з меншим числом значущих цифр. Перевіримо такий ефект, порівнявши результати метода Ньютона з тим алгоритмом, який був викладений у попередньому розділі.
Задача. Знайти корінь рівняння 2∙sin x –x2 +2 = 0 з точністю e = 0,5*10-5. За змістом тут досить знайти будь – який один корінь рівняння. Як уже відомо, існує два корені у відрізках ізоляції [-1;-0,6] і [1,8;2,2]. Обираємо другий: у ньому кількість ітерацій була дещо більшою і дорівнювала 12. 1. Отже [a;b] = [1,8;2,2]. 2. f′ (х) = 2 ∙ cos x – 2x, f′′ (x) = – 2 ∙ sin x – 2 ≤ 0 при всіх х. Отже на [1,8;2,2] знак f′′ (х) не змінюється. 3. З графіку функції у = f (x) бачимо, що f (1,8) > 0, f (2,2) < 0. Тому за початкове наближення можна взяти точку b = 2,2. 4. Відповідна електронна таблиця:
В результаті отримуємо:
Стабілізація знову на п’ятому кроці! Схоже на то, що метод Ньютона більш ефективний, ніж попередні. Формалізуємо це спостереження. Означення. Нехай хk (k = 0,1,2,…) – значення ітерації деякого процесу без урахування похибок обчислень, Якщо α = 1, то кажуть, що ітераційний процес збігається лінійно; якщо α = 2, то квадратично і так далі. Наприклад, якщо хk – це процес простої ітерації, тобто хk = φ(хk-1) (k = 0,1,2,…) і функція φ(х) задовольняє умові Ліпшиця з константою Ліпшиця q, то │хk – х*│ = │φ(хk-1) – φ(х*)│ ≤ q│хk-1 – х*│. Звідси видно, що будь – який процес простої ітерації має принаймні лінійну збіжність.
Теорема 7. Ітераційний процес метода Ньютона збігається квадратично. 1. Спочатку розглянемо довільний процес простої ітерації: хk = φ(хk-1) на відрізку ізоляції [a;b] кореня х*, φ′(х*) = φ′′(х*) = … = φ(m-1)(х*) = 0, φ(m)(х*) ≠ 0. (3) За формулою Тейлора φ(х) – х* = (х – х*)φ′(х*) + │хk – х*│ ≤ С│хk-1 – х*│m, де С = Отже з (3) випливає, що порядок збіжності α процесу хk = φ(хk-1) дорівнює m. 2. Тож для доведення теореми достатньо порахувати похідні функції φ(х) = х – φ′(х*) = (х – φ′′(х*) = ( оскільки у методі Ньютона за умовою f′ (x*) ≠ 0, f′′ (x*) ≠ 0. Теорема доведена. З формули (4) випливає також, що │хk – х*│ ≤ С ∙│хk-1 – х*│2, де С =
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 695; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.130.127 (0.007 с.) |

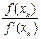 . Знайдене значення х і будемо вважати рівним хk+1:
. Знайдене значення х і будемо вважати рівним хk+1: . Від прикладів попередніх розділів він відрізняється лише тим, що тут λ залежить від х.
. Від прикладів попередніх розділів він відрізняється лише тим, що тут λ залежить від х.



 хk= х*. Порядок збіжності ітераційного процесу – це таке найбільше натуральне число α, що │хk – х*│≤ С│хk-1 – х*│α (k = 0,1,2,…), де С > 0 – деяка стала.
хk= х*. Порядок збіжності ітераційного процесу – це таке найбільше натуральне число α, що │хk – х*│≤ С│хk-1 – х*│α (k = 0,1,2,…), де С > 0 – деяка стала. φ′′(х*) + … +
φ′′(х*) + … +  φ(m-1)(х*) +
φ(m-1)(х*) +  φ(m)(ξ) = =
φ(m)(ξ) = =  [a;b]. Зокрема при х = хk-1, φ(хk-1) = хk маємо хk – х* =
[a;b]. Зокрема при х = хk-1, φ(хk-1) = хk маємо хk – х* =  φ(m)(ξk), де ξk є [хk; x*]
φ(m)(ξk), де ξk є [хk; x*]  │φ(m)(ξ)│ ≠ 0. (4)
│φ(m)(ξ)│ ≠ 0. (4)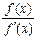 , яка визначає метод Ньютона, у корені х* (f (x*) = 0). Отже
, яка визначає метод Ньютона, у корені х* (f (x*) = 0). Отже │х* =
│х* =  │х* = 0.
│х* = 0. + f(x) ∙ (
+ f(x) ∙ ( )′)│х* =
)′)│х* =  ≠ 0,
≠ 0, │
│ 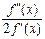 │. Отже, якщо наближення хk-1 має m правильних десяткових знаків, то хk у методі Ньютона щонайменше матиме 2m правильних десяткових знаків. Однак, у теоремі 7 врахована тільки похибка методу і згідно з висновком теореми 6 цей найшвидший збіг триватиме лише доти, доки похибка методу за величиною не зрівняється з похибкою обчислень.
│. Отже, якщо наближення хk-1 має m правильних десяткових знаків, то хk у методі Ньютона щонайменше матиме 2m правильних десяткових знаків. Однак, у теоремі 7 врахована тільки похибка методу і згідно з висновком теореми 6 цей найшвидший збіг триватиме лише доти, доки похибка методу за величиною не зрівняється з похибкою обчислень.


