
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Чисельне інтегрування. Квадратурні формулиСодержание книги
Поиск на нашем сайте
Якщо функція f (х) неперервна на відрізку [a; b] і відома її первісна F, то справедлива формула Ньютона – Лейбниця Означення 1. Квадратурні формули – це формули вигляду Крім похибки методу, тобто залишкового члена Rn(f), треба враховувати й інші похибки розв’язку, згадані в розділі 1. Це, по – перше, так звана неусувна похибка, яка зумовлена наближеними значеннями f (хk). Якщо абсолютні похибки значень f (хk) дорівнюють Δ, то абсолютна похибка квадратурної суми Найпростіші квадратурні формули можна отримати з наочних міркувань. Так, якщо f (х) ≈ const, то на відрізку [a; b] можна покласти I = I = (b – a) f ( Нехай функція f (х) близька до лінійної. Тоді природно замінити інтеграл площею трапеції з висотою b – a та основами f (a) і f (b).
a b
Рисунок 1.
Отримаємо формулу трапецій: I = (b – a) З наочних міркувань ясно, що й формула прямокутників теж дає непоганий результат в цьому випадку: (b – a) f (
Квадратурні формули Ньютона – Котеса Нехай обчислюється інтеграл
D (d0, d1, …, dn) = Отже, ôRn(f)ô ≤ Нехай всі dj різні. Тоді згідно з означенням 3 розділу Ln(х) = Після тої ж заміни х =
Отже, побудована тим самим квадратурна формула має вигляд
Означення 2. 1)Квадратурну формулу (9), коефіцієнти якої Di обчислюють за формулою (8) називають інтерполяційною. 2) Якщо вузли формули (9) рівновіддалені, то інтерполяційна квадратурна формула називається формулою Ньютона – Котеса, а її коефіцієнти Di називаються коефіцієнтами Котеса. Наведемо декілька елементарних квадратурних формул – прикладів цієї конструкції. 1. Формула прямокутників. Нехай n = 0, d0 = 0. Тоді згідно з (6) D(d0) = 2. Формула трапецій. Нехай n = 1, d0 = – 1, d1 = 1. Тоді згідно з (6) D(d0, d1) = Аналогічно можна отримати й оцінку ôR(f)ô ≥ 3. Формула Сімпсона. Нехай n = 3, d0 = – 1, d1 = 0, d2 = 1, d3 = 0. Тоді згідно з (6) D (d0, d1, d2, d3) = Згідно з теоремою 2.2 розділу L3(x) – L2(x) = f (x0; x1; x2; x3)(х – x0)(х – x1)(х – x2) = f (a; b;
Аналогічно можна отримати й оцінку ôR(f)ô ≥
|
|||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 513; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.234.56 (0.008 с.) |

 . Проте цією формулою неможливо скористатися, якщо первісну F не можна виразити у відомих (традиційно в елементарних) функціях, або якщо функцію f задано таблично або графічно. У цих випадках необхідно будувати методи для наближеного обчислення визначених інтегралів. Найчастіше застосовують квадратурні формули.
. Проте цією формулою неможливо скористатися, якщо первісну F не можна виразити у відомих (традиційно в елементарних) функціях, або якщо функцію f задано таблично або графічно. У цих випадках необхідно будувати методи для наближеного обчислення визначених інтегралів. Найчастіше застосовують квадратурні формули. ≈
≈  . Суму в правій частині формули
. Суму в правій частині формули  . Треба враховувати також похибку обчислення R2, що виникає за рахунок округлення проміжних результатів. Отже, повна похибка чисельного інтегрування R дорівнює R = Rn(f) + R1 + R2.
. Треба враховувати також похибку обчислення R2, що виникає за рахунок округлення проміжних результатів. Отже, повна похибка чисельного інтегрування R дорівнює R = Rn(f) + R1 + R2. ).
).

 f (a)
f (a) f (b)
f (b)
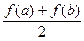 .
. dj (j = 0, 1, …, n). Шукаємо
dj (j = 0, 1, …, n). Шукаємо  . Звідси Rn(f) =
. Звідси Rn(f) =  . Різницю f (х) – Ln(х) можна оцінити, скориставшись оцінкою похибки інтерполяційного многочлена Лагранжа Ln(х) (теорема 1 розділу 2): Rn(f, x) =
. Різницю f (х) – Ln(х) можна оцінити, скориставшись оцінкою похибки інтерполяційного многочлена Лагранжа Ln(х) (теорема 1 розділу 2): Rn(f, x) =  ωn+1(х), де ξ = ξ (x) є [a; b], ωn+1(х) = (x – x0)(x – x1)…(x – xn). Звідси ôRn(f)ô ≤
ωn+1(х), де ξ = ξ (x) є [a; b], ωn+1(х) = (x – x0)(x – x1)…(x – xn). Звідси ôRn(f)ô ≤  )
)  . Замінимо змінну в останньому інтегралі: х =
. Замінимо змінну в останньому інтегралі: х =  = D(d0, d1, …, dn) (
= D(d0, d1, …, dn) ( . (6)
. (6) f (xi).
f (xi). , Di =
, Di =  . (8)
. (8) = 1, згідно з (8) D0 =
= 1, згідно з (8) D0 =  = 2. Отже, згідно з (9) маємо квадратурну формулу
= 2. Отже, згідно з (9) маємо квадратурну формулу 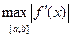 ) (
) ( =
=  =
=  . Згідно з (8) D0 =
. Згідно з (8) D0 =  =
=  = 1, D1 =
= 1, D1 =  = 1. Отже, згідно з (9) справді маємо квадратурну формулу трапецій:
= 1. Отже, згідно з (9) справді маємо квадратурну формулу трапецій:  )
)  =
=  .
.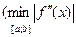 )
) 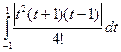 =
=  =
= 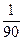 .
. = 0; тому
= 0; тому  =
=  . Многочлен L2(x) = f (x0; x1; x2)(х – x0)(х – x1) = f (a; b;
. Многочлен L2(x) = f (x0; x1; x2)(х – x0)(х – x1) = f (a; b;  =
= 
 =
=  , D1 =
, D1 =  =
=  =
=  , D2 =
, D2 =  =
=  =
=  (f (a) + 4 f (
(f (a) + 4 f ( )
)  .
. )
) 


