
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Пошук початкового опорного розв’язку. Метод штучного базисуСодержание книги
Поиск на нашем сайте
Для того, щоби застосувати симплекс – метод до задачі лінійного програмування у канонічній формі, необхідно спочатку знайти деякий початковий допустимий опорний розв’язок. У попередньому прикладі це було досягнуто завдяки безпосередньому розповсюдженню симплекс – метода (метода жорданових перетворень). Розглянемо це більш докладно на прикладі задачі про раціон, математична модель якої отримана у §1: f = 20х1 + 30х2 (min)
Ввівши нові змінні х3, х4 і змінивши знаки коефіцієнтів у цільової функції, зведемо цю модель до канонічної: f ´ = – 20х1 – 30х2 (mах)
Запишемо її у електронну симплекс – таблицю:
Ця симплекс – таблиця не приведена до початкового опорного розв’язку. Проте будемо діяти у відповідності з симплекс – методом. Змінні x3, x4 не можна безпосередньо використати у якості основних, оскільки тоді їх значення будуть від’ємними, а відповідні розв’язки не допустимими. Спробуємо x1 у якості основної. Щоби знайти ведучий елемент у стовпці А перевіримо умову допустимості.
Отже, виокремимо нову симплекс – таблицю в діапазоні А6: F8. Надамо чарункам електронної таблиці таких значень:
Звичайно, спочатку діємо у рядку 7, а потім у решті. В результаті дістанемо:
У якості другої основної змінної спробуємо x2. Щоби знайти ведучий елемент у стовпці В перевіримо умову допустимості.
Нам пощастило: ведучий елемент виявився саме на необхідному місці. Якщо б замість 3,666667 значення у чарунці В6 дорівнювало скажімо 0,1, то нам залишилося б замість x2 спробувати якусь іншу змінну. Тепер виконаємо чергове жорданове перетворення з ведучим елементом у В6:
Нарешті симплекс – таблиця виявляється приведеною до базису А1, А2 опорного розв’язку. Всі оцінки не додатні. Згідно з теоремою 1 це означає, що розв’язок є оптимальним, на цьому симплекс – метод припиняє роботу. Значення цільової функції із зміненими коефіцієнтами f ´ = – 27,27273, отже f = 27,27273. Разом з тим зауважимо, що оцінка δ3 = 0, отже цільова функція, виражена через вільні змінні х4, х3 має вигляд f ´ = 27,27 – 5,45х4. Тому, якщо обрати за нову основну змінну х3, то хоча її значення і стане додатним замість нульового, але значення цільової функції f ´ не зміниться і ми дістанемо новий оптимальний опорний розв’язок. Отже, виконаємо жорданове перетворення ще раз. У стовпці С додатним є лише значення у чарунці С11, тому вона і є ведучим елементом. В результаті дістанемо:
Отже, існують принаймні два різних оптимальних опорних розв’язка, а тому існує нескінченна множина оптимальних розв’язків даної задачі – всі точки на відрізку між цими опорними розв’язками. Загалом процес перетворень виглядає так:
Звичайно, застосований тут метод не є ефективним алгоритмом пошуку початкового опорного розв’язку. Фактично ми просто пробували деякі пари змінних у якості основних і такий процес перебору може тривати дуже довго. Справжнім ефективним алгоритмом є наступний метод штучного базису.
Розглянемо задачу лінійного програмування у канонічній формі (3): f =
xj ≥ 0 (j = 1, 2, …, n).
Як і завжди, вважаємо, що всі bi ≥ 0. Для пошуку початкового опорного розв’язку побудуємо допоміжну задачу g =
xj ≥ 0 (j = 1, 2, …, n), yi ≥ 0 (i = 1, 2, …, m). (4)
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 340; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.241.124 (0.008 с.) |

 .
. .
. (max)
(max)
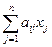 = bi (i = 1, 2, …, m)
= bi (i = 1, 2, …, m) (min)
(min)


