
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розділ 7. Чисельні методи розв’язування звичайних диференціальних рівняньСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Метод Ейлера Звичайним диференціальним рівнянням називають таке рівняння, що зв’язує незалежну змінну х, невідому функцію у(х) і її похідні у´, у´´, …, у(n). Загальний вигляд звичайного диференціального рівняння F(x, y, у´, у´´, …, у(n)) = 0. Його порядок – це порядок вищої похідної, що входить до нього. Розв’язком диференціального рівняння є дозвільна функція у(х), підстановка якої у це рівняння перетворює його у тотожність. Наприклад, у´ = cos x – звичайне диференціальне рівняння першого порядку. Воно еквівалентне твердженню, що функція у(х) є первісною cos x і отже у(х) = Означення 1. Задача Коші для звичайного диференціального рівняння першого порядку у´ = f (x, y); у(х0) = у0 (1) полягає в тому, щоб знайти розв’язок у(х) цього рівняння, який задовольняє початкову умову у(х0) = у0. Геометрично це означає, що треба знайти ту інтегральну криву у(х) рівняння у´ = f (x, y), яка проходить через точку (х0; у0). Теорема (існування та єдності розв’язку задачі Коші для звичайного диференціального рівняння першого порядку). Якщо функція f (x, y) і її часткова похідна Отже, на відміну від квадратного рівняння диференціальне рівняння практично завжди має розв’язок і при тому єдиний. Насправді, проінтегрувати диференціальне рівняння у скінченому вигляді, “на папері” вдається дуже рідко, лише для певних спеціальних класів рівнянь. Фактично здебільшого застосовують наближене інтегрування. Мабуть найкращий шлях зрозуміти теорему існування та єдності диференціального рівняння – це розібрати найстаріший та найпростіший метод його чисельного інтегрування – метод Ейлера.
Означення 2. 1) Розв’язати задачу Коші (1) чисельно означає для заданої послідовності х0, х1, …, хn значень незалежної змінної х і числа у0 знайти числову послідовність у0, у1, …, уn так, щоб уk з заданою точністю наближав у(хk) для всіх k, де у(х) – єдиний розв’язок задачі Коші з початковою умовою у(х0) = у0. 2) Різницю уk – у(хk) називають похибкою наближеного значення уk в точці хk. 3) Якщо всі точки х0, х1, …, хn рівновіддалені: хk = х0 + kh, то величину h називають кроком інтегрування диференціального рівняння. Спочатку зауважимо, що оскільки кутовий коефіцієнт дотичної до інтегральної кривої у(х) у точці (хk; уk) дорівнює у´ = f (хk; уk), то рівняння дотичної у (хk; уk) матиме вигляд у – уk = f (хk; уk)(х – хk). Геометричний зміст диференціального рівняння у´ = f (x, y) в тому, що воно визначає напрям інтегральної кривої в кожній точці площини в деякому околі початкової точки (х0; у0). Отже, рівняння дотичної у початковій точці М0(х0; у0) має вигляд у – у0 = f (х0; у0)(х – х0). Зафіксуємо крок інтегрування h і на цій дотичній знайдемо точку М1(х1; у1) з х1 = х0 + h. Звідси у1 = у0 + f (х0; у0)h. Рівняння дотичної у М1(х1; у1) – це у – у1 = f (х1; у1)(х – х1). На цій дотичній точка М2(х2; у2) з абсцисою х2 = х1 + h = х0 + 2h має ординату у2 = у1 + f (х1; у1)h, …. На дотичній у точці Мk(хk; уk), де хk = х0 + kh обираємо точку Мk+1(хk+1; уk+1), де хk+1 = хk + h = х0 + (k+1)h, звідки уk+1 = уk + f (хk; уk)h. В результаті дістанемо ламану, яка сполучає точки Мk(хk; уk) відрізками дотичних і наближено зображує інтегральну криву шуканого розв’язку y(x) задачі Коші. Її назва – ламана Ейлера (див. рисунок 1).
y(x)
М5
x0 h h h h h h h h
Рисунок 1
Отже, метод Ейлера – це ітераційний метод, рекурентна формула якого має вигляд: xk+1 = xk + h, уk+1 = уk + f (хk; уk)h (k = 0, 1, 2, …, n – 1). (2) Зазначимо, що оскільки ламана Ейлера складається з відрізків дотичних, то похибка наближеного значення уk на кожному кроці k є величина порядку O(h2). З переходом від точки до точки ця похибка систематично зростає і на відрізку завдовжки одиниця сумарна похибка є величиною порядку O(h), оскільки ітерацій з кроком інтегрування h на такому відрізку порядку
Очевидною причиною похибки на кожному кроці є те, що нахил інтегральної кривої неперервно змінюється в той час як нахил ламаної Ейлера є незмінним на кроці. Тому можна сподіватись, що похибка дещо зменшиться, якщо на кожному кроці нахил відрізку дотичної буде співпадати з нахилом інтегральної кривої не на початку, а в середині кроку. Точніше кажучи, спочатку за формулою (1) знайти точку М(хk + ½; уk + ½) посередині відрізку МkМk+1: хk+½ = хk +
yk
xk xk + ½ xk + 1
Рисунок 2.
Такий дещо модифікований алгоритм називають удосконаленим методом Ейлера. Отже, його рекурентну формулу можна записати так: уk + ½ = уk + Чи справді таке удосконалення призведе до помітного зменшення похибки? Несподівано виявляється, що похибка наближеного значення уk на кожному кроці k є величиною порядку O(h3) і отже на відрізку завдовжки одиниця сумарна похибка є величиною порядку O(h2) (на відміну від О(h) для методу Ейлера).
|
||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 493; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.38.165 (0.012 с.) |

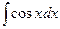 = sin x + C, де С – довільна стала. Цей приклад з’ясовує традиційну термінологію: звичайно розв’язування диференціального рівняння ще називають інтегруванням, його розв’язок – інтегралом, а графік розв’язку – інтегральною кривою. Ще один приклад: у´ = 2у – це теж звичайне диференціальне рівняння першого порядку, його розв’язок у(х) = Се2х, де С – довільна стала. В цьому можна переконатись прямою підстановкою згідно з означенням розв’язку. В обох прикладах розв’язок залежить не тільки від х, але й від довільної сталої. Розв’язок виявиться єдиним, якщо він додатково задовольняє початкову умову у(х0) = у0. Так у першому прикладі, якщо у(0) = 0, то у(х) = sin x – єдиний розв’язок. Якщо у(0) = 1, то у(х) = е2х – це єдиний розв’язок у другому прикладі.
= sin x + C, де С – довільна стала. Цей приклад з’ясовує традиційну термінологію: звичайно розв’язування диференціального рівняння ще називають інтегруванням, його розв’язок – інтегралом, а графік розв’язку – інтегральною кривою. Ще один приклад: у´ = 2у – це теж звичайне диференціальне рівняння першого порядку, його розв’язок у(х) = Се2х, де С – довільна стала. В цьому можна переконатись прямою підстановкою згідно з означенням розв’язку. В обох прикладах розв’язок залежить не тільки від х, але й від довільної сталої. Розв’язок виявиться єдиним, якщо він додатково задовольняє початкову умову у(х0) = у0. Так у першому прикладі, якщо у(0) = 0, то у(х) = sin x – єдиний розв’язок. Якщо у(0) = 1, то у(х) = е2х – це єдиний розв’язок у другому прикладі. (x, y) неперервні у точці (х0; у0), то існує єдиний розв’язок у(х) рівняння у´ = f (x, y), який задовольняє початкову умову у(х0) = у0.
(x, y) неперервні у точці (х0; у0), то існує єдиний розв’язок у(х) рівняння у´ = f (x, y), який задовольняє початкову умову у(х0) = у0. y
y

 М2 O(h)
М2 O(h)



 O(h2) М1 М3 М8
O(h2) М1 М3 М8
 М7
М7




 y0 М6
y0 М6 x
x . Коли h ® 0, то ламана Ейлера з початковою умовою у(х0) = у0 збігається до інтегральної кривої єдиного розв’язку задачі Коші для диференціального рівняння з такою початковою умовою.
. Коли h ® 0, то ламана Ейлера з початковою умовою у(х0) = у0 збігається до інтегральної кривої єдиного розв’язку задачі Коші для диференціального рівняння з такою початковою умовою. h, уk + ½ = уk +
h, уk + ½ = уk +  y Mk+1
y Mk+1 L
L yk + ½ Mk+½
yk + ½ Mk+½
 x
x f (хk; уk); уk+1 = уk + f (хk +
f (хk; уk); уk+1 = уk + f (хk + 


