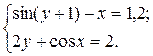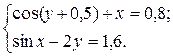Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розв’язок систем лінійних рівняньСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
ВСТУП
Сучасна обчислювальна техніка вимагає від інженерів знання основ обчислювальної математики (чисельних методів) та застосування цих знань до вирішення різних практичних задач. Обчислювальна математика – одна з основних дисциплін, що необхідна для підготовки спеціалістів, які працюють в різних галузях науки та господарчо-промислового комплексу. Дані методичні вказівки є керівництвом до виконання курсової роботи, присвяченої важливому розділу обчислювальної математики, а саме чисельним методам розв’язку систем рівнянь. Вказівки складено на основі лекційного курсу у відповідності до робочої навчальної програми для студентів денної форми навчання напрямів підготовки 6.050201 «Системна інженерія», спеціалізація «Системи управління та автоматика» та 6.050903 «Телекомунікації», спеціалізація «Телекомунікаційні системи та мережі». Розділ обчислювальної математики, що розглядається, обумовив таку структуру роботи. Частина 1 присвячена методам розв’язку систем лінійних рівнянь. Розглянуто методи перевірки існування розв’язку; прямі методи розв’язку, такі як метод зворотної матриці, метод Крамера, методи Гауса; числові методи розв’язку – уточнення коренів, простої ітерації, Зейделя. Частина 2 вказівок містить числові методи розв’язку систем нелінійних рівнянь, а саме метод Ньютона, метод ітерацій та Зейделя. В частині 3 розглянуто числові методи розв’язку задачі Коші для систем диференціальних рівнянь (ДР), а також рівнянь вищих порядків, розв’язок яких зводиться до розв’язку систем ДР. Наведено методи Ейлера, Рунге-Кута, багатокрокові методи Адамса. Крім того, наведено метод розв’язку крайової задачі для рівняння ІІ порядку. Додаток містить вимоги до оформлення пояснювальної записки до курсової роботи відповідно до стандартів ДСТУ 3008-95. Також під час виконання курсової роботи студентам необхідно наводити алгоритми згідно з ГОСТ 19.701-90. Розв’язок систем лінійних рівнянь
Постановка задачі
Система з
Сукупність коефіцієнтів цієї системи запишемо у виді таблиці
Дана таблиця з Використовуючи поняття матриці
де
Сукупність чисел
Для існування єдиного розв’язку системи лінійних рівнянь (1.1) необхідно і достатньо, щоб визначник матриці
Методи розв’язку систем лінійних рівнянь поділяються на дві групи – прямі та ітераційні. Прямі (точні) методи використовують кінцеві співвідношення (формули) для обчислення невідомих. Вони дають розв’язок після виконання наперед відомого числа операцій. Приклади цих методів: метод зворотної матриці, метод Крамера, метод Гауса. Ітераційні методи – це методи послідовних наближень, що вимагають деякого початкового наближення. За допомогою певного алгоритму проводиться один цикл обчислень, який називається ітерацією. Після виконання ітерації буде знайдено нове наближення. Ітерації проводяться до одержання розв’язку з необхідною точністю. До цієї групи методів належать, наприклад, метод простих ітерацій і метод Зейделя.
Метод зниження порядку
Полягає в обчисленні Мінором Алгебраїчним доповненням
Властивість 9. Визначник дорівнює сумі добутків елементів будь-якого рядка (стовпця) на їхні алгебраїчні доповнення.
Ця властивість називається розкладанням визначника по елементах рядка (стовпця). Використовуючи наведені властивості, можна зручно обчислювати визначники вищих порядків. Метод зниження порядку – добитися, щоб в деякому рядку (стовпці) стало якомога більше нулів, і розкласти визначник по елементах цього рідка (стовпця). Зрозуміло, що формула (1.4) значно спрощується, якщо всі крім одного елементи рядку або стовпця дорівнюють 0 (метод ефективного зниження порядку).
Прямі методи
Метод Крамера
Згідно даного методу кожне невідоме системи (1.1) представляється у виді відношення визначників. Запишемо його для системи рівнянь порядку
Тоді
де В методі Крамера необхідно обчислити (
Метод зворотної матриці
Якщо система рівнянь – невироджена, тобто визначник матриці системи За умови
або
Формула (1.5) дає розв’язок рівняння (1.3).
Метод Гауса
– За схемою одиничного ділення Метод заснований на приведенні матриці системи Зворотний хід методу Гауса полягає в послідовному обчисленні невідомих: розв’язуючи останнє рівняння, знаходимо єдине невідоме Розглянемо схему застосування методу Гауса для системи з трьох рівнянь:
Для виключення де
Помноживши друге рівняння системи (1.7) на де
Система (1.8) має трикутний вид. На цьому закінчується прямий хід методу Гауса. Зазначимо, що в процесі виключення невідомих, доводиться виконувати операції ділення на коефіцієнти Зворотний хід починається з рішення третього рівняння системи (1.8):
Використовуючи це значення, можна знайти
Аналогічно будується обчислювальний алгоритм для лінійної системи з довільним числом рівнянь.
– З вибором головного елементу Ця модифікація методу Гауса полягає в тому, що вимога нерівності 0 коефіцієнтів
– За схемою Жордана Також є модифікацією метода Гауса. В цьому випадку матриця системи Алгоритм розв’язку системи (1.1) методом Гауса-Жордана. 1. Нехай 2. Перевірити, чи відмінний діагональний елемент 3. Якщо відмінний, то 4. Для
де
аналогічно представимо нові праві частини рівнянь:
5. Збільшуємо
6. Обчислення вектора-розв’язку
– Метод прогонки Модифікація методу Гауса. Цей метод використовується для розв’язку частинного випадку розріджених систем лінійних рівнянь – рівнянь з тридіагональною матрицею. Такі системи виникають при числовому розв’язку крайових задач для диференціальних рівнянь. Запишемо систему рівнянь в виді:
де Метод прогонки складається з двох етапів – прямої прогонки (аналог прямого ходу методу Гауса) та зворотної прогонки (аналогу зворотного ходу методу Гауса). Пряма прогонка полягає в вираженні кожного невідомого
З першого рівняння
Оскільки З другого рівняння:
Так само Аналогічно можна обчислити прогоночні коефіцієнти для будь-якого
де Отже,
Далі виконується зворотна прогонка, для чого спочатку обчислюється
Потім
та формулами прогоночних коефіцієнтів. Під час обчислення
Числові методи
Метод уточнення коренів
Цей метод дозволяє уточнити розв’язок, отриманий за допомогою прямого методу. Метод уточнення коренів дає можливість зменшити помилки обчислень, а саме помилки округлення. Розглянемо систему лінійних рівнянь (1.1):
Нехай за допомогою будь-якого прямого методу (наприклад, методу Гауса), були обчислені наближені значення невідомих
Введемо позначення Віднімаючи з вихідної системи систему рівнянь з наближеними значеннями коренів, отримаємо таку систему:
Розв’язуючи цю систему знаходимо значення похибок
В той самий спосіб можна знайти поправки до розв’язку Зазначимо, що для знаходження певного значення похибок (поправок) розв’язуються системи лінійних рівнянь з тією самою матрицею
Метод простої ітерації
Проілюструємо цей метод на прикладі розв’язку системи:
Збіжність даного методу гарантується, якщо діагональні елементи
причому хоча б для одного рівняння нерівність має виконуватися строго. Зазначимо, що будь-які системи лінійних рівнянь можна звести до потрібного для збіжності виду за допомогою лінійних перетворень (додавання, вирахування, множення на константу) над рівняннями системи. Припустимо, що для даної системи умова збіжності виконується. Виразимо невідомі
Задамо деякі початкові (нульові) наближення значень невідомих. В якості нульових значень можуть бути обрані: стовпець вільних членів Підставляючи ці значення в праву частину рівнянь системи (1.10), одержуємо нове (перше) наближення для невідомих
Використовуючи обчислені значення
Ітераційний процес продовжується доти, поки значення
або критерієм по відносних відхиленнях (при
де Описаний алгоритм може бути розширений на систему з
Метод Зейделя
Ітераційний метод Зейделя відрізняється від методу простої ітерації тим, що на
Зазначені вище умова збіжності та умова припинення обчислень для методу простої ітерації залишаються вірними для методу Зейделя.
Завдання
Розв’язати систему лінійних рівнянь: 1) прямими методами (зворотної матриці, Крамера, Гауса) з двома знаками після коми; 2) уточнити отриманий в п. 1) розв’язок числовими методами (уточнення коренів, ітерацій або Зейделя) з точністю 3) Навести блок-схеми алгоритмів використаних методів.
Постановка задачі Багато практичних задач зводиться до розв’язку систем нелінійних рівнянь. На відміну від систем лінійних рівнянь, не існує прямих методів розв’язку нелінійних систем. Загальний метод розв’язку системи рівнянь має складатися з двох етапів: відділення коренів і подальшого уточнення розв’язку. Для одержання розв’язку звичайно використовуються ітераційні методи. Вибір первинних наближень впливає на збіг ітераційного процесу; вони мають бути досить близькими до точного розв’язку. У протилежному випадку ітераційний процес може не збігтися. Первинне наближення знаходять графічно (для випадку двох рівнянь із двома невідомими) або іншими методами (аналітичними, методом проб) для систем з великою кількістю рівнянь. Розглянемо систему нелінійних рівнянь:
У матричному виді:
де
Метод Ньютона і методи простої ітерації та Зейделя є ітераційними методами. Метод Ньютона має велику швидкість збігу. У той же час метод простої ітерації має більш прості умови збіжності і є менш критичним до вибору первинного наближення. Тому для високоточних обчислень рекомендується застосовувати спочатку метод простої ітерації. Після того, як знайдені наближення, досить близькі до точних, використовувати метод Ньютона. Числові методи розв’язку Метод Ньютона
Якщо знайдені
де Розкладаючи ліву частину
у ряд Тейлора, обмежуючись лінійними членами розкладання, одержуємо систему лінійних рівнянь відносно виправлень:
Розв’язувати отриману систему лінійних рівнянь можна будь-яким методом з розглянутих в розділі 1. При розв’язанні системи методом зворотної матриці отримаємо рекурентну формулу для обчислення виправлень, а звідси і формулу ітераційного процесу визначення розв’язку системи (2.1) або (2.2), яка отримала назву методу Ньютона:
де
Якщо в формулі (2.5) матрицю, зворотну до матриці Якобі, обчислювати на кожній ітерації в фіксованій початковій точці Процес ітерації (2.5) триває доти, поки не буде справедлива нерівність:
де Зауваження Метод Ньютона ефективний тільки при достатній близькості первинного наближення до розв’язку системи. Вимоги до збіжності методу досить жорсткі, теореми про швидкість збіжності, стійкість наведені у [7]. Практично метод Ньютона застосовується для уточнення розв’язку, отриманого яким-небудь іншим методом. Матриця Якобі містить частинні похідні першого порядку. Оскільки аналітичне диференціювання в загальних випадках небажано, окремі похідні заміняють їх наближеними кінцево-різницевими значеннями:
Метод простої ітерації
Для розв’язку системи нелінійних рівнянь методом простої ітерації необхідно навести її у виді:
Ітераційний процес реалізується наступними формулами:
Ітераційний процес продовжується доки не буде досягнуте виконання умов (2.11) або (2.12): · критерій з абсолютних відхилень:
· критерій з відносних відхилень (якщо
де Умова збіжності методу визначається формулою
де
матриця частинних похідних правих частин Метод Зейделя
Метод Зейделя є модифікованим методом простої ітерації, на відміну від якого, уточнені значення коренів відразу підставляються в наступні рівняння. Послідовні наближення визначаються із співвідношень:
Все сказане відносно збіжності методу простої ітерації в п. 2.2.2, вірно і для методу Зейделя, тобто умова збіжності залишається такою самою.
Завдання
Розв’язати систему нелінійних рівнянь з точністю до 1) За методом Ньютона отримати систему лінійних рівнянь та розв’язати ії прямим методом з завдання 1.5 п. 1); 2) Розв’язати систему ітераційним методом (ітерацій або Зейделя). Метод вказано в таблиці варіантів; 3) Порівняти результати, отримані за пп. 1) і 2); 4) Навести блок-схеми алгоритмів використаних методів.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 626; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.171.121 (0.009 с.) |

 лінійних алгебраїчних рівнянь з
лінійних алгебраїчних рівнянь з  . (1.1)
. (1.1)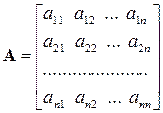 . (1.2)
. (1.2) елементів, що складається з
елементів, що складається з 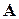 , систему рівнянь (1.1) можна записати в матричному виді:
, систему рівнянь (1.1) можна записати в матричному виді: . (1.3)
. (1.3) и
и  – вектор-стовпець невідомих і вектор-стовпець правих частин відповідно:
– вектор-стовпець невідомих і вектор-стовпець правих частин відповідно: ,
,  .
. (або, коротше, вектор
(або, коротше, вектор 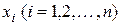 – її коренями.
– її коренями. .
.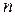 визначників
визначників  -го порядку.
-го порядку. елемента
елемента  визначника
визначника 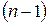 -го порядку, який утворюється з заданого визначника шляхом викреслювання
-го порядку, який утворюється з заданого визначника шляхом викреслювання  -го рядка та
-го рядка та  -го стовпця.
-го стовпця. елемента
елемента  визначника називається відповідний мінор
визначника називається відповідний мінор  , взятий з певним знаком
, взятий з певним знаком
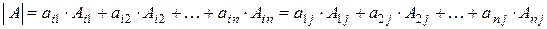 . (1.4)
. (1.4) :
: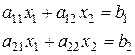
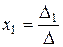 ,
,  ,
, ,
,  ,
,  .
.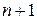 ) визначник
) визначник  , то система (1.1) або еквівалентне їй матричне рівняння (1.3), має єдиний розв’язок.
, то система (1.1) або еквівалентне їй матричне рівняння (1.3), має єдиний розв’язок. . Помноживши обидві частини рівняння (1.3) зліва на матрицю
. Помноживши обидві частини рівняння (1.3) зліва на матрицю 
 . (1.5)
. (1.5) із усіх наступних рівнянь системи. Потім за допомогою другого рівняння перетвореної системи виключається
із усіх наступних рівнянь системи. Потім за допомогою другого рівняння перетвореної системи виключається  із третього і всіх наступних рівнянь. Цей процес, називаний прямим ходом методу Гауса, продовжується доти, поки в лівій частині останнього (
із третього і всіх наступних рівнянь. Цей процес, називаний прямим ходом методу Гауса, продовжується доти, поки в лівій частині останнього ( , тобто матриця системи буде приведена до трикутного виду.
, тобто матриця системи буде приведена до трикутного виду.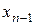 і т.д. Останнім знаходимо
і т.д. Останнім знаходимо  (1.6)
(1.6)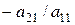 і
і  відповідно. Одержимо рівносильну систему виду:
відповідно. Одержимо рівносильну систему виду: , (1.7)
, (1.7) ,
, 
 ,
, 
 і додавши результат до третього рівняння, виключимо тим самим
і додавши результат до третього рівняння, виключимо тим самим  , (1.8)
, (1.8) ,
, .
. ,
,  і т.д. Тому вони мають бути відмінні від нуля. В іншому випадку необхідно відповідним чином переставити рівняння системи.
і т.д. Тому вони мають бути відмінні від нуля. В іншому випадку необхідно відповідним чином переставити рівняння системи. .
. ,
, .
. замінюється на більш жорстку: зі всіх елементів, що залишилися в
замінюється на більш жорстку: зі всіх елементів, що залишилися в  -му стовпці, необхідно обрати найбільший за модулем, і переставити рівняння системи так, що цей елемент став діагональним.
-му стовпці, необхідно обрати найбільший за модулем, і переставити рівняння системи так, що цей елемент став діагональним. приводиться до діагонального виду, тобто всі елементи, окрім елементів головної діагоналі, дорівнюють 0. Особливих переваг немає: полегшується зворотний хід, проте через збільшення кількості операцій, ускладнюється прямий хід.
приводиться до діагонального виду, тобто всі елементи, окрім елементів головної діагоналі, дорівнюють 0. Особливих переваг немає: полегшується зворотний хід, проте через збільшення кількості операцій, ускладнюється прямий хід. .
.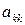 від
від  .
. , то необхідно замінити
, то необхідно замінити  -й (
-й ( ), в якій
), в якій 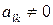 .
. обчислюємо нові матричні елементи, які позначимо, подібно попереднім, за правилом:
обчислюємо нові матричні елементи, які позначимо, подібно попереднім, за правилом: , якщо
, якщо  ,
,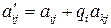 , якщо
, якщо 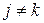 ,
, ;
; .
. , и переходимо до пункту 2. Це приведе до того, що всі елементи
, и переходимо до пункту 2. Це приведе до того, що всі елементи  .
. :
: .
.
 .
. через
через  за допомогою прогоночних коефіцієнтів:
за допомогою прогоночних коефіцієнтів: .
.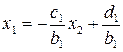 .
. , отже:
, отже: 
 .
. ,
, ,
, ,
, .
. :
: 
 , де
, де 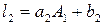 .
. .
.
 ,
, .
.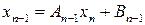 .
. з останнього рівняння:
з останнього рівняння: ,
, ,
, ,
, ,
, .
. за формулою
за формулою та
та  необхідно враховувати можливість ділення на 0. Щоб запобігти цьому бажано, щоб в таких системах виконувалась умова переважання діагональних елементів, тобто
необхідно враховувати можливість ділення на 0. Щоб запобігти цьому бажано, щоб в таких системах виконувалась умова переважання діагональних елементів, тобто 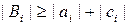 і хоча б для одного
і хоча б для одного 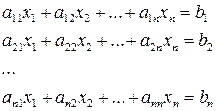 .
. . Підставивши ці розв’язки в ліві частини системи, отримаємо значення
. Підставивши ці розв’язки в ліві частини системи, отримаємо значення  , що відрізняються від
, що відрізняються від 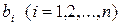 :
: .
. – похибка значень невідомих,
– похибка значень невідомих,  ,
,  .
.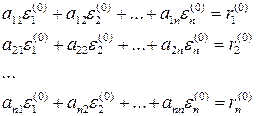 .
. (
(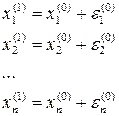 .
. (
( і т.д. Процес продовжується доти, поки всі чергові значення похибок (поправок)
і т.д. Процес продовжується доти, поки всі чергові значення похибок (поправок) 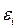 не стануть достатньо малими (такими, що задовольняють нас).
не стануть достатньо малими (такими, що задовольняють нас). не дорівнюють 0 і для них виконується умова:
не дорівнюють 0 і для них виконується умова: ,
, з першого, другого і третього рівнянь системи (1.9) відповідно:
з першого, другого і третього рівнянь системи (1.9) відповідно: . (1.10)
. (1.10) , відношення
, відношення  , а також будь-які інші значення (наприклад, нульові), тому що виконання умови збіжності забезпечує досягнення результату при будь-яких початкових умовах.
, а також будь-які інші значення (наприклад, нульові), тому що виконання умови збіжності забезпечує досягнення результату при будь-яких початкових умовах. . (1.11)
. (1.11) ,
,  ,
,  , можна тим саме способом провести другу ітерацію, у результаті якої будуть знайдені другі наближення до розв’язку
, можна тим саме способом провести другу ітерацію, у результаті якої будуть знайдені другі наближення до розв’язку  ,
,  ,
,  . Наближення з номером
. Наближення з номером  можна представити у виді:
можна представити у виді: . (1.12)
. (1.12) ,
,  ,
,  , не стануть близькими з заданою похибкою до значень
, не стануть близькими з заданою похибкою до значень  ,
,  ,
, 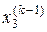 , що можна перевірити критерієм по абсолютних відхиленнях
, що можна перевірити критерієм по абсолютних відхиленнях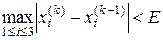 , (1.13)
, (1.13) )
)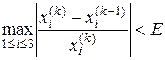 , (1.14)
, (1.14)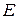 – задана похибка невідомих. При виконанні умови (1.13) або (1.14) процес ітерацій припиняється і за шукані розв’язки приймаються їх останні обчислені значення.
– задана похибка невідомих. При виконанні умови (1.13) або (1.14) процес ітерацій припиняється і за шукані розв’язки приймаються їх останні обчислені значення. використовуються значення
використовуються значення  ,
,  , обчислені на тій самій ітерації. Наближення на
, обчислені на тій самій ітерації. Наближення на  , (1.15)
, (1.15) ;
;











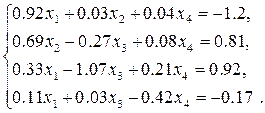




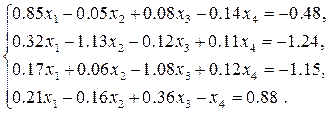


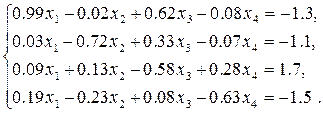








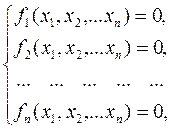 (2.1)
(2.1) (2.2)
(2.2) ,
,  (2.3)
(2.3) , можна записати точний розв’язок
, можна записати точний розв’язок  системи (2.1) у виді:
системи (2.1) у виді: ,
,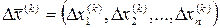 – виправлення до розв’язку, що шукається.
– виправлення до розв’язку, що шукається. (2.4)
(2.4) .
. (2.5)
(2.5) , (2.6)
, (2.6)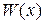 – матриця Якобі,
– матриця Якобі, – матриця, зворотна до матриці Якобі.
– матриця, зворотна до матриці Якобі. замість
замість  (тобто використовуємо зафіксовану зворотну матрицю), отримаємо модифікований метод Ньютона. Очевидно, цей метод вимагає менше обчислень, але й дає меншу точність.
(тобто використовуємо зафіксовану зворотну матрицю), отримаємо модифікований метод Ньютона. Очевидно, цей метод вимагає менше обчислень, але й дає меншу точність. (2.7)
(2.7) , (2.8)
, (2.8) .
. (2.9)
(2.9)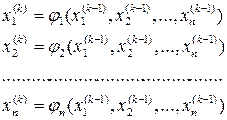 (2.10)
(2.10) (2.11)
(2.11) ):
): (2.12)
(2.12) , (2.13)
, (2.13) ,
,  – перша або друга норма матриці
– перша або друга норма матриці 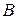 ,
, (2.14)
(2.14) ,
,  , системи (2.9), обчислених у точці первинного наближення
, системи (2.9), обчислених у точці первинного наближення  ,
,  , …,
, …,  .
. (2.15)
(2.15) .
.