
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Рішення лінійної системи методом ГаусаСодержание книги Поиск на нашем сайте
Функція augment(A,b) формує розширену матрицю системи додаванням до матриці системи справа стовпця правих частин. Функція rref приводить розширену матрицю системи до ступінчастого вигляду, виконуючи прямий і зворотний ходи гауссова виключення. Останній стовпець містить рішення системи.
3.3. Решение системы методом Крамера Порядок выполнения работы. 1. Вычисляем D определитель матрицы А. 2. Зададим матрицу DX1, заменой первого столбца матрицы А, матрицей b. Вычисляем определитель матрицы DX1. 3. Зададим матрицу DX2, заменой второго столбца матрицы А, матрицей b. Вычисляем определитель матрицы DX2. 4. Зададим матрицу DX3, заменой третьего столбца матрицы А, матрицей b. Вычисляем определитель матрицы DX3. 5.
Определяем решение системы линейных уравнений x1, x2, x3.
Рішення системи лінійній алгебрі рівняння методом простих ітерацій Порядок виконання завдання 1. Введіть матриці C і d. 2. Преобразуйте исходную систему Cx=d до вигляду x=b+Ax. 3. Визначте нульове наближення рішення. 4. Задайте кількість ітерацій. 5. Обчисліть послідовні наближення. Рішення системи лінійних рівнянь алгебри методом Зейделя Порядок виконання завдання 1. Введіть матриці С і d. 2. Перетворіть систему Cx=d до вигляду x=b+A1x+A2x.
5. Обчисліть послідовні наближення.
Початкові дані для розв’язку рівнянь і систем:
Лабораторна робота №3 Тема: Рішення систем лінійних рівнянь Методи рішення систем лінійних рівнянь
або у векторному вигляді можна розділити на дві основні групи: прямі методи і ітераційні. Прямі методи дають точне рішення за кінцеве число операцій; до них відносяться, наприклад, методи Крамера і Гауса. Ітераційні методи дають рішення системи рівнянь як межу послідовних наближень. Для ітераційних методів необхідне виконання умов збіжності і додаткових перетворень системи в еквівалентну їй.
Завдання 1 1. Вирішити систему лінійних рівнянь методом Гауса. Завдання приведені в таблиці 2. Коментар. Контроль виконуваних обчислень є важливим елементом рішення будь-якої обчислювальної задачі. Для контролю прямого ходу користуються контрольними сумами, які є сумами коефіцієнтів при невідомих і вільного члена для кожного рівняння заданої системи. Для контролю обчислень в основній частині схеми єдиного ділення (стовпці коефіцієнтів при невідомих і вільних членів) над контрольними сумами виконують ті ж дії, що і над рештою елементів того ж рядка. За відсутності обчислювальних помилок контрольна сума для кожного рядка в межах впливах погрішностей округлення і їх накопичення повинна співпадати з рядковою сумою - другим стовпцем контролю. Рядкові суми є сумами всіх елементів з основної частини цього рядка. Завдання 2 Вирішити систему (2.1) методом простій ітерації. Передбачається надалі, що матриця А квадратна і невироджена. Заздалегідь приведемо систему (2.2) до ітераційного вигляду:
Для довільного початкового вектора
сходиться, якщо виконана одна з умов [2] а) б) в) Процес обчислень закінчуємо при виконанні умови де Завдання 3 Вирішити систему (2.1) методом Зейделя. Метод Зейделя відрізняється від методу простій ітерації тим, що знайшовши якесь значення для компоненти, ми на наступному кроці використовуємо його для відшукання наступною компоненти. Обчислення ведуться по формулі Кожна з умов (2.4) -(2.6) є достатнім для збіжності ітераційного процесу по методу Зейделя. Практично ж зручніше наступне перетворення системи (2.2). Домножая обидві частини (2.2) на АТ, одержимо еквівалентну нею систему
где
ПРИБЛИЗНИЙ варіант виконання лабораторної роботи
Приклад. Розв’яжіть систему рівнянь X1+2X2+3X3=7, X1-3X2+2X3=5, X1+X2+X3=3.
|
||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 218; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.174.253 (0.006 с.) |








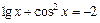



 (перші три корені)
(перші три корені)

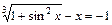



 (перші три корені)
(перші три корені)





 (2.1)
(2.1) (2.2)
(2.2) (2.3)
(2.3) ітераційний процес
ітераційний процес
 (2.4)
(2.4) (2.5)
(2.5) (2.6)
(2.6) (2.7)
(2.7) (i=1,2,3)- одна з метрик, визначувана лівою частиною (2.4)-(2.6), по якій була встановлена збіжність,
(i=1,2,3)- одна з метрик, визначувана лівою частиною (2.4)-(2.6), по якій була встановлена збіжність,  - задана точність (
- задана точність ( ).
). (2.8)
(2.8) ,
, =
=  и d =
и d =  . Далі, поділивши кожне рівняння на, приведемо систему до вигляду (2.8). Подібне перетворення також гарантує збіжність ітераційного процесу.
. Далі, поділивши кожне рівняння на, приведемо систему до вигляду (2.8). Подібне перетворення також гарантує збіжність ітераційного процесу.


