
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Рішення задач лінійної алгебри. Операцї над векторами таСодержание книги
Поиск на нашем сайте
Обчислювальна математика Методичні вказівки до лабораторних робіт
для студентів спеціальностей напрямку 6.100102 "Процеси, машини та обладнання агропромислового виробництва"
Затверджено на засіданні кафедри ОТ і ПМ. Протокол № 1 від 27.08.2010 р.
Кіровоград – 2010 Обчислювальна математика. Методичні вказівки до лабораторних робіт для студентів спеціальностей напрямку 6.100102 "Процеси, машини та обладнання агропромислового виробництва" / К.М. Марченко – Кіровоград: КНТУ, 2010. – 68 с.
Для студентів спеціальностей напрямку 6.100102 "Процеси, машини та обладнання агропромислового виробництва" при вивченні навчальної дисципліни„Обчислювальна математика”. Визначено тематику лабораторних робіт, подано довідку про необхідний для їх виконання обсяг знань, приведені варіанти індивідуальних робіт.
Автор-укладач: Марченко Костянтин Миколайович - канд. техн. наук, доцент кафедри обчислювальної техніки та прикладної математики Зміст Вступ................................................................................................................... 3 Лабораторна робота №1. Метоли дослідження математичних функцій................................................................................................................ 4 Лабораторна робота №2. Рішення задач лінійної алгебри. Операцї над векторами та матрицями....................................................... 8 Лабораторна робота №3. Обчислення коренів поліному. Розв’язування систем лінійних рівнянь...................................................... 12 Лабораторна робота №4. Розв’язування нелінійних рівнянь та систем нелінійних рівнянь.............................................................................. 16 Лабораторна робота №5. Розв’язування дифференційних рівнянь та систем дифференційних рівнянь............................................................. 20 Лабораторна робота №6. Чисельне інтегрування та дифферен-ціювання функцій 24 Лабораторна робота №7. Методи інтерполяції функцій...................... 28 Лабораторна робота №8. Аппроксимація залежностей за масивами даних................................................................................................ 32 Лабораторна робота №9. Рішення задач оптимізаційного типу........ 36 Література......................................................................................................... 40 Вступ Обчислювальна математика (ОМ) - це розділ математики, що включає коло питань, зв'язаних з використанням електронних обчислювальних машин (ЕОМ). Часто термін ОМ розуміється також як теорія чисельних методів і алгоритмів вирішення типових математичних завдань. В ОМ можна виділити наступні три великі розділи. Перший пов'язаний із вживанням ЕОМ в різних областях наукової і практичної діяльності і може бути охарактеризований як аналіз математичних моделей. Другий — з розробкою методів і алгоритмів вирішення типових математичних задач, що виникають при дослідженнях математичних моделей. Третій розділ пов'язаний з питанням про спрощення взаємин людини з ЕОМ, включаючи теорію і практику програмування завдань для ЕОМ, у тому числі автоматизацію програмування завдань. Аналіз математичних моделей включає вивчення постановки задачі, вибір моделі, аналіз і обробку вхідної інформації, чисельне рішення математичних задач, що виникають у зв'язку з дослідженням моделі, аналіз результатів обчислень, і, нарешті, питання, пов'язані з реалізацією отриманих результатів. Використання математичних моделей дозволяє виконувати дослідження не з реаальними об’єктами, наприклад машинами під час їх розробки та удосконалення, а з комп’ютерними програмами, що значно зменшує витрати коштів та часу. Вивчення реальних явищ на основі аналізу побудованих моделей як правило, вимагає розвитку чисельних методів і залучення ЕОМ. Таким чином, в ОМ важливе місце займають чисельні методи вирішення поставлених математичних задач. Як приклад типових задач ОМ можна назвати задачі лінійної алгебри, чисельні методи диференціювання і інтегрування функцій одної або декількох змінних; чисельні методи рішення звичайних диференціальних рівнянь. Значне число досліджень присвячене чисельним методам вирішення рівнянь з частковими похідними. Тут великий напрям складають «економічні методи», тобто методи, що дозволяють отримувати результати при відносно малому (економному) числі операцій. Напрямом ОМ, що швидко розвивається, є чисельні методи оптимізації. Завдання оптимізації полягає у вивченні екстремальних (найбільших або найменших) значень функціоналів на певній множині. Одним із спеціалізованих середовищ для рішення задач обчислювальної математики на ЕОМ є пакет прикладних програм автоматизованих математичних розрахунків MathCad. Робота з документами MATHCAD не вимагає обов'язкового використання можливостей головного меню, оскільки основні з них дублюються кнопками швидкого управління, які розташовані в зручних переміщуваних за допомогою миші набірних панелях-палітрах. Набірні панелі з'являються у вікні редагування документів при активізації кнопок-піктограм. Вони служать для виведення заготовок-шаблонів математичних знаків (цифр, знаків арифметичних операцій, матриць, знаків інтеграла, похідних, границь та ін.). Основні математичні панелі інструментів наведені на рис. 1:
Рисунок 1 – Основні математичні панелі інструментів MathCad Лабораторна робота №1 Рішення задач лінійної алгебри. Операцї над векторами та Матрицями Для дій із векторами та матрицями використовується панель інструментів Matrix:
а також меню команд Symbolics/ Matrix. Приклади операцій над векторами і матрицями можна переглянути у середовищі MathCad Help/ Resource Center/ Quick Sheets/ Vectors and Matrices. Функії для операцій із веторами:
Функії для операцій із матрицями:
Специальні характеристики матриць:
Функції для сортування векторів і матриць:
Завдання: Виконати операції над векторамим та матрицями згідно варіантам (для застосування деяких функцій вектори-рядки при необхідності транспонувати у вектори-стовпці): Таблиця 7 – Початкові дані для обробки векторів і матриць:
Продовження таблиці 7
Таблиця 8 – Приклади дій над векторами і матрицями:
Контрольні питання: 1. Способи створення вектора та матриці у середовищі MathCad. 2. Які інструменти MathCad служать для обробки векторів і матриць? 3. Як відсортувати матрицю за заданим рядком? 4. Як додати у кінець матриці вектор-стовпчик? 5. Що виконує вираз reverse(sort(V))? 6. Як з матриці виділити другий стовпчик у вигляді окремого вектора? 7. Як розрахувати функцію від всіх елементів матриці одночасно? 8. Вивести на екран індекс останнього елемента вектора. З якої цифри починається нумерація елементів вектора або матриці? 9. Як виділити з матриці, що складається з комплексних елементів, дійсну та уявну частини? 10. Як знайти матрицю обернену до заданої? Як обчислити визначник матриці? Лабораторна робота №3 Завдання 1 1. Вирішити систему лінійних рівнянь методом Гауса. Завдання приведені в таблиці 2. Коментар. Контроль виконуваних обчислень є важливим елементом рішення будь-якої обчислювальної задачі. Для контролю прямого ходу користуються контрольними сумами, які є сумами коефіцієнтів при невідомих і вільного члена для кожного рівняння заданої системи. Для контролю обчислень в основній частині схеми єдиного ділення (стовпці коефіцієнтів при невідомих і вільних членів) над контрольними сумами виконують ті ж дії, що і над рештою елементів того ж рядка. За відсутності обчислювальних помилок контрольна сума для кожного рядка в межах впливах погрішностей округлення і їх накопичення повинна співпадати з рядковою сумою - другим стовпцем контролю. Рядкові суми є сумами всіх елементів з основної частини цього рядка. Завдання 2 Вирішити систему (2.1) методом простій ітерації. Передбачається надалі, що матриця А квадратна і невироджена. Заздалегідь приведемо систему (2.2) до ітераційного вигляду:
Для довільного початкового вектора
сходиться, якщо виконана одна з умов [2] а) б) в) Процес обчислень закінчуємо при виконанні умови де Завдання 3 Вирішити систему (2.1) методом Зейделя. Метод Зейделя відрізняється від методу простій ітерації тим, що знайшовши якесь значення для компоненти, ми на наступному кроці використовуємо його для відшукання наступною компоненти. Обчислення ведуться по формулі Кожна з умов (2.4) -(2.6) є достатнім для збіжності ітераційного процесу по методу Зейделя. Практично ж зручніше наступне перетворення системи (2.2). Домножая обидві частини (2.2) на АТ, одержимо еквівалентну нею систему
где
Порядок виконання роботи. КОНТРОЛЬНІ ПИТАННЯ Лабораторна робота №4 Приклад 1
Приклад 2
Обчислити інтеграл від заданої функції на відрізку [a,b] по формулі трапецій і прямим способом. Приклад 1 Вирішити диференціальне рівняння y’=f(x,y) методом Ейлера на відрізку [a,b] з кроком h з початковою умовою y(a)=y0 , f(x,y)=(3x-y)/(x2+y), a=2, b=3, h=0.1, y0=1.
Приклад 2 Вирішити диференціальне рівняння y’=f(x,y) методом Рунге-Кутта на відрізку [a,b] з кроком h з початковою умовою y(a)=y0.
Завдання: Знайти значення визначених інтегралів Таблиця 1
2. Знайти рішення диференціального рівняння y′=f(x,y) методом Ейлера на відрізку [а,b] з кроком h з початковою умовою у(a)=y0, f(x,y)=(3x-y)/(x2+y), a=2, b=3, h=0.1, y0=1. 3. Розв’язати диференціальне рівняння y’=f(x,y) методом Рунге-Кутта на відрізку [а,b] з кроком h з початковою умовою у(a)=y0. Таблиця 2
Лабораторная работа №5 Задание 1 По заданной таблице значений функции составить формулу интерполяционного многочлена Лагранжа (3.2) и построить график
Tаблица 3.1.
Задание 2 Вычислить одно значение заданной функции для промежуточного значения аргумента (
Для погрешности
где Таблица 3.2
Таблица 3.3
Таблица 3.4
Таблица 3.5
Таблица 3.6
Задание 3. Уплотнить часть таблицы заданной на отрезке
где
где Формула (3.5) называется первой интерполяционной формулой Ньютона. Если вычисляемое значение переменной ближе к концу отрезка
где
Таблица 3.7
Таблица 3.8
КОНТРОЛЬНІ ПИТАННЯ 1. У чому особливість наближення табличний заданої функції методом інтерполяції? 2. Як обгрунтовується існування і єдиність інтерполяційного многочлена? 3. Який зв'язаний ступінь інтерполяційного многочлена з кількістю вузлів інтерполяції? 4. Як будуються інтерполяційні многочлени Лагранжа і Ньютона? 5. У чому особливості цих двох способів інтерполяції? 6. Як проводиться оцінка погрішності методу інтерполяції многочленом Лагранжа? 7. Як використовується метод інтерполяції для уточнення таблиць функцій? 8. У чому відмінність між першою і другою інтерполяційними формулами Ньютона?
Лабораторна робота №6 Завдання 1 У MathCad побудувати методом найменших квадратів дві емпіричні формули: лінійну і квадратичну. У разі лінійної функції
а у разі квадратичної залежності
Вибрати з двох функцій найбільш відповідну. Для цього скласти таблицю для підрахунку суми квадратів відхилень по формулі:
Приклад 1:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 317; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.42.247 (0.012 с.) |








 V1+V2
V1+V2
 X+Y
X+Y
 T+U
T+U
 Z+S
Z+S
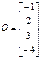 R+O
R+O
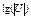






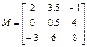



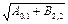









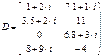



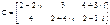
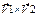
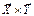
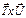


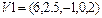



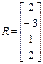
 V1+V2
V1+V2
 X+Y
X+Y
 T+U
T+U
 Z+S
Z+S
 R+S
R+S
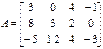
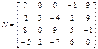









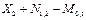
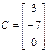





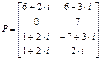
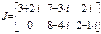

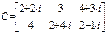


 (2.3)
(2.3) ітераційний процес
ітераційний процес
 (2.4)
(2.4) (2.5)
(2.5) (2.6)
(2.6) (2.7)
(2.7) (i=1,2,3)- одна з метрик, визначувана лівою частиною (2.4)-(2.6), по якій була встановлена збіжність,
(i=1,2,3)- одна з метрик, визначувана лівою частиною (2.4)-(2.6), по якій була встановлена збіжність,  - задана точність (
- задана точність ( ).
). (2.8)
(2.8) ,
, =
=  и d =
и d =  . Далі, поділивши кожне рівняння на, приведемо систему до вигляду (2.8). Подібне перетворення також гарантує збіжність ітераційного процесу.
. Далі, поділивши кожне рівняння на, приведемо систему до вигляду (2.8). Подібне перетворення також гарантує збіжність ітераційного процесу.




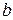


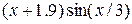




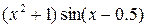





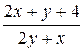







 Исходные данные берутся из таблицы 3.1.
Исходные данные берутся из таблицы 3.1.
 +
+ 
 +
+ 
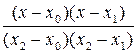 (3.2)
(3.2)


 (3.3)
(3.3)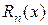 выполняется неравенство
выполняется неравенство ,
,  (3.4)
(3.4)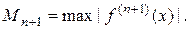


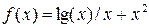


 функции, используя интерполяционный многочлен Ньютона (3.5) и оценить погрешность интерполяции D (формула (3.6)). Таблицу 3.7 конечных разностей просчитать вручную на отрезке
функции, используя интерполяционный многочлен Ньютона (3.5) и оценить погрешность интерполяции D (формула (3.6)). Таблицу 3.7 конечных разностей просчитать вручную на отрезке  +
+ 
 3 y 0, (3.5)
3 y 0, (3.5) .
. , (3.6)
, (3.6)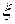 – некоторая внутренняя точка наименьшего промежутка, содержащего все узлы
– некоторая внутренняя точка наименьшего промежутка, содержащего все узлы  и x.
и x. , то применяют вторую формулу Ньютона – интерполирование назад (формула (3.6)).
, то применяют вторую формулу Ньютона – интерполирование назад (формула (3.6)).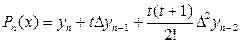 +
+ 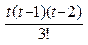

 3 y n-3 (3.6)
3 y n-3 (3.6)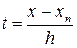 и
и 




 =
= 


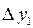 =
= 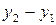


 =
= 



 задача зводиться знаходженню параметрів
задача зводиться знаходженню параметрів 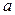 і
і  із системи лінійних рівнянь
із системи лінійних рівнянь , де
, де ,
,  ,
,  , My=
, My=  i
i до знаходження параметрів
до знаходження параметрів  із системи рівнянь:
із системи рівнянь: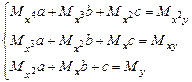 , де
, де ,
,  ,
, 


 Варіанти завдань:
Варіанти завдань:
 №
№



