
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема: Интерполирование функцийСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть функция Классический подход к решению задачи построения приближающей функции основывается на требование строгого совпадения значений
В этом случае нахождение приближенной функции называют интерполяцией (или интерполированием), точки Часто интерполирование ведется для функций, заданных таблицами с равноотстоящими значениями аргумента
Задание 1 По заданной таблице значений функции составить формулу интерполяционного многочлена Лагранжа (3.2) и построить график
Tаблица 3.1.
Задание 2 Вычислить одно значение заданной функции для промежуточного значения аргумента (
Для погрешности
где Таблица 3.2
Таблица 3.3
Таблица 3.4
Таблица 3.5
Таблица 3.6
Задание 3. Уплотнить часть таблицы заданной на отрезке
где
где Формула (3.5) называется первой интерполяционной формулой Ньютона. Если вычисляемое значение переменной ближе к концу отрезка
где
Таблица 3.7
Таблица 3.8
Приблизний фрагмент виконання роботи
КОНТРОЛЬНІ ПИТАННЯ 1. У чому особливість наближення табличний заданої функції методом інтерполяції? 2. Як обгрунтовується існування і єдиність інтерполяційного многочлена? 3. Який зв'язаний ступінь інтерполяційного многочлена з кількістю вузлів інтерполяції? 4. Як будуються інтерполяційні многочлени Лагранжа і Ньютона? 5. У чому особливості цих двох способів інтерполяції? 6. Як проводиться оцінка погрішності методу інтерполяції многочленом Лагранжа? 7. Як використовується метод інтерполяції для уточнення таблиць функцій? 8. У чому відмінність між першою і другою інтерполяційними формулами Ньютона?
Лабораторна робота №6 Тема: Апроксимація залежностей методом найменших квадратів Завдання 1 У MathCad побудувати методом найменших квадратів дві емпіричні формули: лінійну і квадратичну. У разі лінійної функції
а у разі квадратичної залежності
Вибрати з двох функцій найбільш відповідну. Для цього скласти таблицю для підрахунку суми квадратів відхилень по формулі:
Приклад 1:
Реалізація методу найменших квадратів в табличному процесорі Microsoft Excel: Завдання 2 Визначити математичну залежність кількості виїздів пожежних частин від календарного року, використовуючи метод найменших квадратів. Скласти прогноз на 2011 рік. У наведених залежностях n – число пар точок х та у. Коефіцієнт а знаходимо у клітині В11 за формулою: =(7*СУММПРОИЗВ($B$3:$H$3;$B$4:$H$4)-СУММ($B$4:$H$4)* СУММ($B$3:$H$3))/(7*СУММПРОИЗВ($B$3:$H$3;$B$3:$H$3)-СУММ($B$3:$H$3)^2). Коефіцієнт b знаходимо у клітині В12 за формулою: =(СУММ($B$4:$H$4)-B11*СУММ($B$3:$H$3))/7. Перевірку знайденої залежності виконуємо шляхом порівняння значень у діапазонах B4:H4 I B14:H14. Похибку можна оцінити в процентах за формулою: =ABS(B4-B14)/B4*100 для кожної пари значень або графічно. Прогноз на 2008 рік знаходимо в клітині В17 за формулою =В11*В16+В12.
Множинна лінійна регресія Приклад 2. Припустимо, що забудовник оцінює вартість групи невеликих офісних будинків у традиційному діловому районі. Забудовник може використовувати множинний регресійний аналіз для оцінки ціни офісного будинку в заданому районі на основі наступних змінних.
У цьому прикладі передбачається, що існує лінійна залежність між кожної незалежної перемінною (x1, x2, x3 і x4) і залежної перемінний (y), тобто ціною будинку під офіс у даному районі. Забудовник навмання вибирає 11 будинків з наявних 1500 і одержує наступні дані.
Рисунок 18 – Таблиця статистичних даних «Пів-входу» (1/2) означає вхід тільки для доставки кореспонденції. Виділяємо клітини А14:Е18 і вводимо у них як масив приведену нижче функцію: ЛИНЕЙН(E2:E12;A2:D12;ИСТИНА;ИСТИНА)Функція повертає наступні результати:
Обчислені коефіцієнти рівняння регресії Рівняння множинної регресії y = m1*x1 + m2*x2 + m3*x3 + m4*x4 + b тепер може бути отримане з рядка 14: y = 27,64*x1 + 12530*x2 + 2553*x3 - 234,24*x4 + 52318 Тепер забудовник може визначити оцінну вартість будинку під офіс у тім же районі, що має площу 2500 квадратних метрів, три офіси, два входи, будинку 25 років, використовуючи наступне рівняння y = 27,64*2500 + 12530*3 + 2553*2 - 234,24*25 + 52318 = 158 261. Завдання 3 1. Підібрати залежність ціни автомобіля від початкової ціни, року випуску, пробігу та оцінки стану у балах:
Виконати перевірку знайденої залежності за рядками таблиці. Обчислити похибку за кожним рядком у процентах. Побудувати графіки поточної ціни за табличними даними та розраховані за знайденою залежністю.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 611; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.140.196.222 (0.012 с.) |

 задана таблично, либо вычисление ее требует громоздких выкладок. Заменим приближенно функцию
задана таблично, либо вычисление ее требует громоздких выкладок. Заменим приближенно функцию  , так, чтобы отклонение
, так, чтобы отклонение  и
и  (
( , т. е.
, т. е. . (3.1)
. (3.1) – узлами интерполяции.
– узлами интерполяции. . В этом случае шаг таблицы
. В этом случае шаг таблицы 
 является величиной постоянной. Для таких таблиц построение интерполяционных формул (как, впрочем, и вычисление по этим формулам) заметно упрощается.
является величиной постоянной. Для таких таблиц построение интерполяционных формул (как, впрочем, и вычисление по этим формулам) заметно упрощается. Исходные данные берутся из таблицы 3.1.
Исходные данные берутся из таблицы 3.1.
 +
+ 
 +
+ 
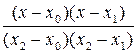 (3.2)
(3.2)



 ) с помощью интерполяционного многочлена Лагранжа (3.3) и оценить погрешность интерполяции. Для выполнения задания исходные данные берутся из таблицы 3.2, 3.3 или 3.4.
) с помощью интерполяционного многочлена Лагранжа (3.3) и оценить погрешность интерполяции. Для выполнения задания исходные данные берутся из таблицы 3.2, 3.3 или 3.4.
 (3.3)
(3.3)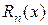 выполняется неравенство
выполняется неравенство ,
,  (3.4)
(3.4)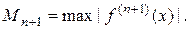

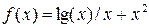


 функции, используя интерполяционный многочлен Ньютона (3.5) и оценить погрешность интерполяции D (формула (3.6)). Таблицу 3.7 конечных разностей просчитать вручную на отрезке
функции, используя интерполяционный многочлен Ньютона (3.5) и оценить погрешность интерполяции D (формула (3.6)). Таблицу 3.7 конечных разностей просчитать вручную на отрезке 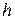 . Для выполнения задания исходные данные берутся из таблиц 3.8, 3.5 и 3.6.
. Для выполнения задания исходные данные берутся из таблиц 3.8, 3.5 и 3.6. +
+ 
 3 y 0, (3.5)
3 y 0, (3.5) .
. , (3.6)
, (3.6)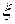 – некоторая внутренняя точка наименьшего промежутка, содержащего все узлы
– некоторая внутренняя точка наименьшего промежутка, содержащего все узлы  и x.
и x. , то применяют вторую формулу Ньютона – интерполирование назад (формула (3.6)).
, то применяют вторую формулу Ньютона – интерполирование назад (формула (3.6)).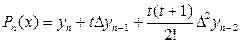 +
+ 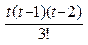

 3 y n-3 (3.6)
3 y n-3 (3.6)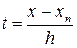 и
и 




 =
= 


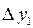 =
= 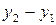


 =
= 


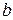

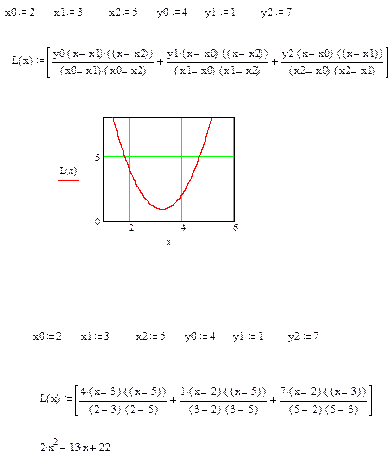
 задача зводиться знаходженню параметрів
задача зводиться знаходженню параметрів 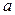 і
і  із системи лінійних рівнянь
із системи лінійних рівнянь , де
, де ,
,  ,
,  , My=
, My=  i
i до знаходження параметрів
до знаходження параметрів  із системи рівнянь:
із системи рівнянь: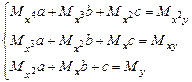 , де
, де ,
,  ,
, 


 Варіанти завдань:
Варіанти завдань:
 №
№






