Задаємо область пошуку максимуму усередині блоку given

 

Знаходимо максимум функції в заданій області

У разі функції однієї змінної задаємо функцію і початкове наближення

Знаходимо максимум

Якщо ми хочемо знайти максимальне або мінімальне значення функції на деякому інтервалі, то необхідно визначити цей інтервал в блоці given

На приведеному нижче графіку видно, що перший із знайдених максимумів відповідав випадку, коли похідна звертається в нуль; другий максимум лежить на межі інтервалу.

Оптимізація в табличному процесорі Excel

Приклад 1. Визначення оптимального плану виробництва

В умовах ринкових відносин планування виробництва передбачає вивчення попиту на продукцію та визначення обсягів випуску продукції, за яких буде отриманий максимальний прибуток. Розглянемо типовий приклад. Підприємство виготовляє чотири види виробів – насос шестеренчастий, гідромотор, гідроциліндр, гідророзподілювач. Відома кількісна оцінка ресурсів підприємства: сировини, фінансів, праці, які задіяні на виготовлення одного виробу відповідного виду, відома також вартість реалізації кожного виробу (готової продукції): числові дані наведені в таблиці 1. При виготовленні названих виробів, необхідно виходити із наявних ресурсів. Задача полягає в тому, щоб визначити, яку кількість яких виробів треба виготовити, щоб отримати максимальний прибуток

Таблиця 1 – Початкові дані

Категорія	Найменування виробів	Умова	Наявність ресурсу
Насос	Мотор	Циліндр	Розпо-ділювач
Прибуток					max	-
Ресурс	Праця					£
Сировина					£
Фінанси					£

Стосовно ситуації, що аналізується, математична модель задачі матиме такий вигляд:

F=60*X₁+70*X₂+120*X₃+130*X₄ ® MAX

1*X₁ + 1*X₂ + 1*X₃ + 1*X₄ £ 16

6*X₁ + 5*X₂ + 4*X₃ + 3*X₄ £ 110

4*X₁ + 6*X₂ +10*X₃ +13*X₄ £ 100.

Для розв’язку цієї задачі в Excel необхідно виконати наступні дії.

Рисунок 10 – Перший крок: створюємо форму для уведення умов задачі

Рисунок 11 – Другий крок: уводимо початкові дані.

Третій крок: уводимо залежності.

А) Уведення залежностідля цільової функції.

Клітину F6 виберемо як базову, у яку згодом буде поміщено максимальне значення цільової функції. Зафіксувавши її, здійснюємо виклик кнопки “Мастер функций” і вибираємо функцію СУММПРОИЗВ із категорії «Математические». У полі «Массив1» вказуємо блок клітин $В$3:$Е$3, до яких буде введено шукані змінні x(1),x(2),x(3),x(4), у полі «Массив2» – блок клітин В6:Е6, у яких указано коефіцієнти цільової функції.

Б) Уведення лівих частин системи обмежень.

Блок клітин F9:F11 виберемо базовими для лівих частин обмежень. До них також заносяться формули, аналогічні формулі з клітини F6. Для цього досить виставити курсор «миші» на клітину F6 і скопіювати вміст її до блоку клітин F9:F11. Тоді база даних матиме наступний вигляд

Рисунок 12 – Третій крок: уводимо залежності

Четвертий крок: пошук розв’язку задачі.

Для знаходження розв’язку потрібно відкрити діалогове вікно “ Поиск решения ” з меню “ Сервис ”. У поле вікна “Установить целевую функцию” вказати клітину, яку вибрано як базову, тобто F6, а нижче – установити перемикач на одному з напрямків цієї функції. А до поля “Изменяя ячейки” потрібно ввести адреси шуканих змінних – B3:E3:

Після натиску кнопки “Добавить” відкривається діалогове вікно «Добавление ограничения», до якого вносяться граничні умови окремо для кожної змінної B3>=B4, C3>=C4, D3>=D4, E3>=E4 а також для F9<=H9, F10<=H10, F11<=H11 через кнопку «Добавить».

Після введення останнього обмеження здійснити натиск кнопки OK. При цьому вікно «Поиск решения» з граничними умовами матиме наступний вигляд:

Рисунок 13 – Четвертий крок: пошук розв’язку задачі

Кінцевим результатом роботи є наступна таблиця:

Рисунок 14 – Результати оптимізації

Розглянуті методи оптимізації можуть бути застосовані також у математиці, наприклад, для розв’язування рівнянь.

Приклад 2

Ілюструє розв’язування квадратного рівняння х² + 4 ∙ х + 2 = 0 за допомогою таких методів: а) теорема Вієтта; б) команда Данные/ Под-бор параметра; в) команда Данные/ Поиск решения. Виконана графічна перевірка знайдених коренів х1 = -3,14 та х2 = -0,59.

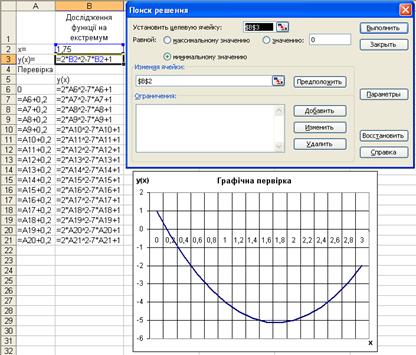
Рисунок 15 – Методи розв’язування рівнянь

Приклад 3

Відшукати екстремум (мінімальне значення) функції 2 ∙ х² – 7 ∙ х + 1.

Рисунок 16 – Пошук екстремуму функції

Завдання:

1. Знайти екстремуми функцій в MathCad/

2. Мале мебельне підприємство виготовляє стільці та крісла. Вартість стільця А гривень, вартість крісла В гривень. Для їх виробництва використовуються матеріали трьох найменувань, які є на складі: с1 кг матеріалу першого найменування, с2 кг – другого та с3 кг третього найменування. Витрати цих матеріалів складають: на стілець – а1 кг матеріалу першого найменування, а2 кг – другого, а3 кг третього найменування; на крісло, відповідно, матеріалу першого найменування - в1 кг, другого – в2 кг, третього – в3 кг. Встановити такий план випуску виробів, щоб підприємство від їх реалізації одержало максимальний прибуток.

 

Варіанти завдань:

Вар.	А1	а2	а3	в1	в2	в3	с1	с2	с3	А	В

3. Розв’язати рівняння та знайти екстремум функції в Excel:

Вар.	Вигляд рівняння	Вигляд функції
	2·х^2 - 5·х + 1 = 0	F(x)= 2·х^2- 5·х + 1
	х^2- 8·х + 2 = 0	F(x)= х^2- 8·х + 2
	-2·х^2 - 6·х - 1 = 0	F(x)= -2·х^2 - 6·х - 1
	4·х^2 + 12·х - 3 = 0	F(x)= 4·х^2 + 12·х - 3
	3·х^2 - 15·х + 4 = 0	F(x)= 3·х^2 - 15·х + 4
	-4·х^2 - 25·х + 11 = 0	F(x)= -4·х^2 - 25·х + 11
	7·х^2 + 14·х - 2 = 0	F(x)= 7·х^2 + 14·х - 2
	х^2 - 6·х + 2 = 0	F(x)= х^2 - 6·х + 2 = 0
	-2·х^2 - 15·х + 7 = 0	F(x)= -2·х^2 - 15·х + 7
	12·х^2 + 15·х + 1 = 0	F(x)= 12·х^2 + 15·х + 1
	6·х^2 - 17·х + 4 = 0	F(x)= 6·х^2 - 17·х + 4
	-3·х^2 + 5·х + 1 = 0	F(x)= -3·х^2 + 5·х + 1
	8·х^2 - 15·х - 2 = 0	F(x)= 8·х^2 - 15·х - 2
	2·х^2 + 13·х + 4 = 0	F(x)= 2·х^2 + 13·х + 4
	-2·х^2 + 5·х -1 = 0	F(x)= -2·х^2 + 5·х -1

Контрольні питання:

1. Що називається оптимізацією?

2. Дати визначення цільової функції.

3. Що таке впливові фактори? На що вони впливають?

4. Що називається системою обмежень?

5. Охарактеризувати декілька сучасних методів оптимізації.

6. Для чого застосовується команда «Сервис/ Поиск решения»? Описати порядок використання методу «Поиск решения».

7. Для чого використовується «Сервис/ Підбор параметра»? Описати порядок використання методу «Поиск решения».

8. Чим відрізняються методи «Поиск решения» і «Підбор параметра»?

9. Як розв’язати нелінійне рівняння в табличному процесорі Ecxel?

10. Як виконати графічну перевірку знайдених у табличному процесорі Ecxel коренів рівняння?

 

 

Література

1. Плис А.И., Сливина Н.А. Mathcad: математический практикум. – М.: Финансы и Статистика. – 1999.

2. Очков В.Ф.. MathCad 7 Pro для студентов и инженеров. – М.: КомпьютерПресс, 1998. – 384 с.

3. Дьяконов В.П. Справочник по MathCAD PLUS 7.0 PRO. – М.: CK Пресс, 1998. – 352 c.

4. Дьяконов В. П., Абраменкова И. В. MathCAD 7 в математике, в физике и в Internet. – М.: Нолидж.- 1998. – 352 с.

5. Тейлор Дж. Введение в теорию ошибок. Пер. с англ. – М.: Мир, 1985. – 272 с., ил.

6. Ортега Дж., Пул У. Введение в численные методы решения дифференциальных уравнений/ Пер. с англ.; Под ред. А. А. Абрамова. – М.: Наука. Гл. физ.-мат. лит., 1986. – 288 с.

7. Заварыкин В. М., Житомирский В. Г., Лапчик М. П. Численные методы: Учеб. пособие для студентов физ.-мат. спец. пед. ин-тов. – М.; Просвещение, 1990. – 176 с.

8. Демидович Б. П., Марон И. А. Основы вычислительной математики. – М.: Наука. Гл. ред. физ.-мат. лит., 1966.

9. Демидович Б. П., Марон И. А., Шувалова Э. З. Численные методы анализа. – М.: Наука. Физматгиз, 1962.