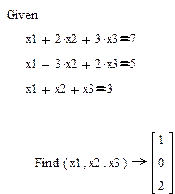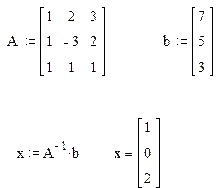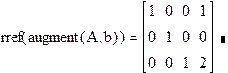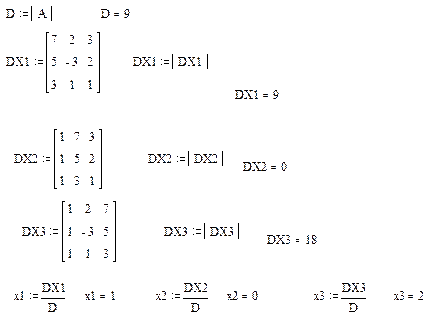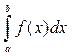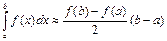Символьне рішення систем рівнянь

Фрагмент робочого документа з відповідними обчисленнями приведений нижче. Тут = - логічна рівність.

 

2. Рішення системи лінійних рівнянь алгебри як матричне рівняння Ax=b

Порядок виконання завдання.

1. Встановіть режим автоматичних обчислень.

2. Введіть матрицю системи і матрицю-стовпчик правих частин.

3. Обчисліть рішення системи за формулою x=A^-1b.

4. Перевірте правильність рішення множенням матриці системи на вектор-стовпець рішення.

5. Знайдіть рішення системи за допомогою функції lsolve і порівняйте результати.

Вирішимо систему за допомогою функції lsolve і порівнянний результат з рішенням x=A^-1b.

Рішення лінійної системи методом Гауса

Коментарі. Функція augment(A,b) формує розширену матрицю системи додаванням до матриці системи справа стовпця правих частин. Функція rref приводить розширену матрицю системи до ступінчастого вигляду, виконуючи прямий і зворотний ходи гауссова виключення. Останній стовпець містить рішення системи.

Рішення системи методом Крамера

Порядок виконання роботи.

Обчислюваний D визначник матриці А.

Задамо матрицю DX1, заміною першого стовпця матриці А, матрицею b. Обчислюємо визначника матриці DX1.

Задамо матрицю DX2, заміною другого стовпця матриці А, матрицею b. Обчислюємо визначника матриці DX2.

Задамо матрицю DX3, заміною третього стовпця матриці А, матрицею b. Обчислюємо визначника матриці DX3.

5. Визначаємо рішення системи лінійних рівнянь x_1, x₂, x₃.

 

 

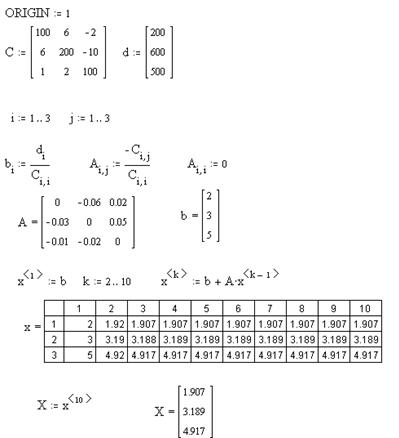
Рішення системи лінійній алгебрі рівняння методом простих ітерацій

Порядок виконання завдання

1. Введіть матриці C і d.

2. Перетворіть початкову систему Cx=d к виду x=b+Ax.

3. Визначте нульове наближення рішення.

4. Задайте кількість ітерацій.

5. Обчисліть послідовні наближення.

Рішення системи лінійних рівнянь алгебри методом Зейделя

 

Порядок виконання завдання

1. Введіть матриці С і d.

2. Перетворіть систему Cx=d до вигляду x=b+A1x+A2x.

3. Визначте нульове наближення рішення.

4. Задайте кількість ітерацій.

Обчисліть послідовні наближення.

 

Таблица 2

№ вар.
	0.35 0.12 - 0.13	0.12 0.71 0.15	- 0.13 0.15 0.63	0.10 0.26 0.38
	0.71 0.10 - 0.10	0.10 0.34 0.64	0.12 - 0.04 0.56	0.29 0.32 - 0.10
	0.34 - 0.04 0.06	- 0.04 0.44 0.56	0.10 - 0.12 0.39	0.33 - 0.05 0.28
	0.10 - 0.04 - 0.43	- 0.04 0.34 0.05	- 0.63 0.05 0.13	- 0.15 0.31 0.37
	0.63 0.05 0.15	0.05 0.34 0.10	0.15 0.10 0.71	0.34 0.32 0.42
	1.20 - 0.50 - 0.30	- 0.20 1.70 0.10	0.30 - 1.60 - 1.50	- 0.60 0.30 0.40
	0.30 - 0.10 - 1.50	1.20 - 0.20 - 0.30	- 0.20 1.60 0.10	- 0.60 0.30 0.70
	0.20 0.58 0.05	0.44 - 0.29 0.34	0.91 0.05 0.10	0.74 0.02 0.32
	6.36 7.42 1.77	1.75 19.03 0.42	1.0 1.75 6.36	41.70 49.49 27.67
	3.11 - 1.65 0.60	- 1.66 3.15 0.78	- 0.60 - 0.78 - 2.97	- 0.92 2.57 1.65

КОНТРОЛЬНІ ПИТАННЯ

До якого типу - прямому або ітераційному - відноситься метод Гауса?

У чому полягає прямий і зворотний хід в схемі єдиного ділення?

Як організовується, контроль над обчисленнями в прямому і зворотному ході?

Як будується ітераційна послідовність для знаходження рішення системи лінійних рівнянь?

Як формулюється достатні умови збіжності ітераційного процесу?

Як ці умови пов'язані з вибором метрики простору?

У чому відмінність ітераційного процесу методу Зейделя від аналогічного процесу методу простій ітерації?

Лабораторна робота №4

Тема:Чисельне інтегрування і диференціювання

Обчислення визначених інтегралів

Хай потрібно обчислити визначений інтеграл на інтервалі [a;b].

Далеко не завжди завдання може бути вирішене аналітично. Зокрема, чисельне рішення потрібне у тому випадку, коли подинтегральная функція задана табличний. Для чисельної інтеграції подинтегральную функцію апроксимують якій-небудь більш простій функцією, інтеграл від якої може бути обчислений. Зазвичай як апроксимуюча функція використовують поліном. У разі полінома нульового ступеня метод чисельної інтеграції називають методом прямокутників, у разі полінома першого ступеня - методом трапецій, у разі полінома другого ступеня - методом Симпсона. Всі ці методи є окремими випадками формул квадратури Ньютона-котеса.

Отже, в методі трапецій подинтегральную функцію апроксимують поліномом першого ступеня, тобто прямою лінією. Це означає, що замість площі криволінійної трапеції ми шукатимемо площу прямокутної трапеції. Наближене значення інтеграла рівне