
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференциальное исчисление функций нескольких переменныхСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть каждой упорядоченной паре чисел Геометрически область определения функции обычно представляет собой некоторую часть плоскости Пример 2.1. Найти область определения
Если переменной
Аналогично, если переменная
Если существуют пределы:
они называются частными производными функции Замечание 2.1. Аналогично определяются частные производные функций любого числе независимых переменных. Замечание 2.2. Так как частная производная по любой переменной является производной по этой переменной при условии, что остальные переменные – постоянны, то все правила дифференцирования функций одной переменной применимы для нахождения частных производных функций любого числа переменных. Пример 2.2. Найти частные производные функции Решение. Находим:
Пример 2.3. Найти частные производные функции Решение. Находим:
Полным приращением функции
Главная часть полного приращения функции
где Аналогично для функции трех переменных
Пусть функция Замечание 2.3. Символ « Пример 2.4. Найти градиент функции Решение. Найдем частные производные:
и вычислим их значения в точке
Следовательно,
Производной функции
Если функция
где В случае функции трех переменных
где Пример 2.5. Найти производную функции Решение. Найдем вектор
Вычислим значения частных производных в точке
Подставляя в (2.1), получаем
Частными производными второго порядка называют частные производные, взятые от частных производных первого порядка:
Частные производные Пример 2.6. Найти частные производные второго порядка функции Решение. Вычислим предварительно частные производные первого порядка:
Продифференцировав их еще раз, получим:
Сравнивая последние выражения, видим, что Пример 2.7. Доказать, что функция
Решение. Находим:
Тогда
Точка
Максимум или минимум функции называется ее экстремумом. Точка, в которой достигается экстремум функции, называется точкой экстремума функции.
Теорема 2.1 (Необходимые условия экстремума). Если точка Точки, для которых эти условия выполнены, называются стационарными, или критическими. Точки экстремума всегда являются стационарными, но стационарная точка может и не быть точкой экстремума. Чтобы стационарная точка была точкой экстремума, должны выполняться достаточные условия экстремума. Введем предварительно следующие обозначения:
Теорема 2.2 (Достаточные условия экстремума). Пусть функция 1. Если 2. Если 3. Если Пример 2.8. Исследовать на экстремум функцию Решение. Так как в данном случае частные производные первого порядка всегда существуют, то для нахождения стационарных (критических) точек решим систему:
откуда Находим:
Для точки Дифференциальные уравнения Рассмотрим основные виды дифференциальных уравнений первого порядка.
|
|||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 1044; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.200.6 (0.012 с.) |

 из некоторой области
из некоторой области  соответствует определенной число
соответствует определенной число  . Тогда
. Тогда 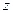 называется функцией двух переменных
называется функцией двух переменных  и
и  ,
,  - независимыми переменными или аргументами,
- независимыми переменными или аргументами,  всех значений функции - областью ее значений и обозначают
всех значений функции - областью ее значений и обозначают  .
.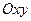 , ограниченную линиями, которые могут принадлежать или не принадлежать этой области.
, ограниченную линиями, которые могут принадлежать или не принадлежать этой области.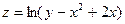 .
.
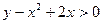 , или
, или  . Точки плоскости, для которых
. Точки плоскости, для которых  , образуют границу области
, образуют границу области  .
.
 , а
, а 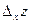 , называемое частным приращением функции
, называемое частным приращением функции 
 , а
, а 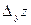 , называемое частным приращением функции
, называемое частным приращением функции 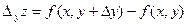 .
. ,
, ,
, .
. ,
, .
. .
. ,
, ,
,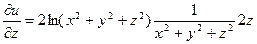 .
. .
.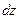 . Если функция имеет непрерывные частные производные, то полный дифференциал существует и равен
. Если функция имеет непрерывные частные производные, то полный дифференциал существует и равен ,
, ,
,  - произвольные приращения независимых переменных, называемые их дифференциалами.
- произвольные приращения независимых переменных, называемые их дифференциалами. полный дифференциал определяется выражением
полный дифференциал определяется выражением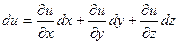 .
. имеет в точке
имеет в точке  частные производные первого порядка по всем переменным. Тогда вектор
частные производные первого порядка по всем переменным. Тогда вектор 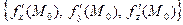 называется градиентом функции
называется градиентом функции  или
или 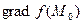 .
. » называется оператором Гамильтона и произносится «намбла».
» называется оператором Гамильтона и произносится «намбла». в точке
в точке  .
. ,
, 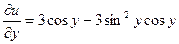 ,
, 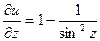
 ,
, 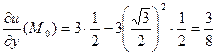 ,
, 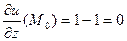 .
. .
.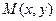 по направлению вектора
по направлению вектора  называют предел отношения
называют предел отношения 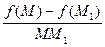 при
при  :
: , где
, где  .
. дифференцируема, то производная в данном направлении вычисляется по формуле
дифференцируема, то производная в данном направлении вычисляется по формуле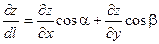 ,
, ,
,  - углы, который вектор
- углы, который вектор  образует с осями
образует с осями  и
и  соответственно.
соответственно. ,
,
 - направляющие косинусы вектора
- направляющие косинусы вектора  в точке
в точке  в направлении вектора
в направлении вектора  , где
, где  .
.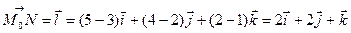 ,
, 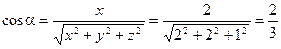 ,
,  ,
,  .
. ,
, 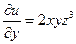 ,
, 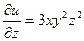 ;
; 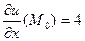 ,
, 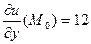 ,
,  .
. .
. ,
, ,
, ,
,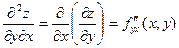
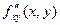 ,
,  называются смешанными. Значения смешанных производных равны в тех точках, в которых эти производные непрерывны.
называются смешанными. Значения смешанных производных равны в тех точках, в которых эти производные непрерывны.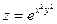 .
. ,
,  .
. ,
, 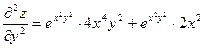 ,
, ,
,  .
. .
. .
. ,
,  .
. ,
, 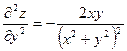 .
.
 .
. называется точкой локального максимума (минимума) функции
называется точкой локального максимума (минимума) функции  (
( ).
).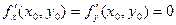 или хотя бы одна из этих производных не существует.
или хотя бы одна из этих производных не существует. ,
,  ,
, 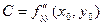 ,
,  .
. , то точка
, то точка  будет точкой максимума при
будет точкой максимума при 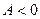 (
( ) и точкой минимума при
) и точкой минимума при  (
( ).
). , то в точке
, то в точке 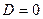 , то экстремум может быть, а может и не быть.
, то экстремум может быть, а может и не быть.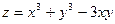 .
. ,
,  ,
, ,
,  ,
, 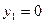 ,
,  . Таким образом, получили две стационарные точки:
. Таким образом, получили две стационарные точки: 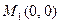 ,
,  .
. ,
,  ,
,  .
. , то есть в этой точке экстремума нет. Для точки
, то есть в этой точке экстремума нет. Для точки 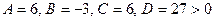 и
и 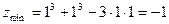 .
.


