
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Системы функций алгебры логикиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Любая булева функция может быть представлена аналитически одной из вышерассмотренных нормальных форм, которые используют ограниченное число элементарных булевых функций. Например, для СДНФ такими функциями являются "конъюнкция", "дизъюнкция" и "отрицание". Следовательно, существуют системы булевых функций, с помощью которых можно аналитически представить любую сколь угодно сложную булеву функцию. Проектирование цифровых автоматов основано на знании таких систем булевых функций. Последнее особенно важно для определения набора элементарных логических схем, из которых можно построить произвольный цифровой автомат. Проблема функциональной полноты является центральной проблемой функциональных построений в алгебре логики. Функционально полной системой булевых функций (ФПСБФ) называется совокупность таких булевых функций (f1, f2,... fk), посредством которых можно записать произвольную булеву функцию f. Это обусловливает целесообразность постановки задачи определения свойств, которыми должны обладать функции, составляющие ФПСБФ. Решение этой задачи основано на понятии замкнутого относительно операции суперпозиции класса функций. Класс булевых функций, функционально замкнутый по операции суперпозиции, есть множество функций, любая суперпозиция которых дает функцию, также принадлежащую этому множеству. Среди функционально замкнутых классов выделяют классы обычного типа, называемые предполными, которые обладают следующими свойствами. Предполный класс S не совпадает с множеством Р всех возможных булевых функций, однако если в него включить любую не входящую в S булеву функцию, то новый функционально замкнутый класс будет совпадать с множеством Р. Проведенные исследования показали, что предполных классов пять, а для построения ФПСБФ необходимо и достаточно, чтобы ее функции не содержались полностью ни в одном из пяти предполных классов. Наряду с нормальными формами представления функций алгебры логики в вычислительной технике широко используются логические полиномиальные формы. Преобразования над формулами булевых функций иногда удобно выполнять в алгебре Жегалкина. Алгебра Жегалкина включает две двухместные операции: конъюнкцию и сложение по модулю 2, а также константу 1. Теорема Жегалкина. Любая функция алгебры логики может быть представлена многочленом вида
где ki – коэффициент, принимающий значения 0 или 1. Теорема позволяет представить любую ФАЛ в виде полиномов различной степени. Задача построения полинома Жегалкина сводится к нахождению коэффициентов ki. Для любых конституент единицы k1 и k2 имеет место следующее соотношение: k1 + k2 = k1 Å k2. Оно позволяет выполнить переход от СДНФ к полиному Жегалкина. Для этого достаточно заменить в СДНФ символ + (дизъюнкции) на символ Å и выполнить подстановку вида х=х Å 1 с последующими преобразованиями в алгебре Жегалкина.
Класс линейных функций. Функция алгебры логики называется линейной, если ее можно представить полиномом первой степени:
Примем без доказательства утверждение, что при суперпозиции линейных функций получаем линейную функцию. Существует восемь линейных функций от двух переменных (табл.10). Следовательно, в функционально полном базисе должна содержаться хотя бы одна нелинейная логическая функция. Класс функций, сохраняющих ноль. К булевым функциям, сохраняющим константу 0, относят такие булевы функции f(x1,...,xn), для которых справедливо соотношение f(0,...,0)=0. Класс функций, сохраняющих единицу. К булевым функциям, сохраняющим константу 1, относят такие булевы функции f(x1,...,xn), для которых справедливо соотношение f(1,...,1)=1. Таблица 10
Класс монотонных функций. Функция алгебры логики называется монотонной, если при любом возрастании набора аргументов значения этой функции не убывают.Двоичный набор A=<a1,a2,...,an> не меньше двоичного набора B=<b1,b2,...,bn>, если для каждой пары (ai,bi) i = 1...n справедливо соотношение ai ≥ bi. Если у двух наборов есть и большие и меньшие аргументы f(0,1) и f(1,0), то наборы считаются несравнимыми. Таким образом, если f(0,0)≥f(0,1) ≥ f(1,1) или f(0,0) ≥f(1,0) ≥f(1,1), то функция f является монотонной. Класс самодвойственных функций. Булевы функции f1(x1,...,xn) и f2(x1,...,xn) называются двойственными друг другу, если выполняется соотношение К самодвойственным булевым функциям относят такие булевы функции, которые двойственны по отношению к самим себе, то есть булева функция называется самодвойственной, если на любых двух противоположных наборах х1,х2,…,хn и Любая ФАЛ, полученная с помощью операции суперпозиции и подстановки из функций одного класса, принадлежит этому же классу. Базисом называется полная система ФАЛ, с помощью которой любая ФАЛ может быть представлена суперпозиций исходных функций. ТеоремаПоста−Яблонского. Для того чтобы система ФАЛ была полной, необходимо и достаточно, чтобы она содержала хотя бы одну функцию: не являющуюся линейной; не сохраняющую ноль; не сохраняющую единицу; не являющуюся монотонной; не являющуюся самодвойственной. Иначе говоря, система булевых функций является функционально полной тогда и только тогда, когда она целиком не содержится ни в одном из предполных классов. Рассмотрим примеры ФПСБФ. Для удобства изложения материала сведем элементарные булевы функции двух переменных и некоторые функции одной переменной в таблицу (табл.11), классифицируя каждую из них по признакам принадлежности к предполным классам. Таблица 11
Из таблицы видно, что каждая из функций F8 и F14 является ФПСБФ. Иными словами, используя, например, только булеву функцию F14 - "штрих Шеффера", можно записать в виде формулы любую булеву функцию. Признаком функциональной полноты, очевидно, является наличие плюса в каждом столбце таблицы, хотя бы для одной из составляющих систему булевых функций. К таким ФСПБФ, наиболее распространенным в практике построения цифровых автоматов, следует отнести: {Λ,V,не}, { Λ,Å,не}, { Λ,Å,1}, { Λ,не}, {V,не}. Иногда удобно строить ФПСБФ при наличии констант, то есть булевых функций "константа 0", "константа 1". Как следует из таблицы, функция "константа 0" несамодвойственна и не сохраняет 1; функция "константа 1" несамодвойственна и не сохраняет 0. Вместе с тем константы являются линейными и монотонными функциями. Отсюда непосредственно (на основании теоремы о функциональной полноте) вытекает следующее: система булевых функций является ослабленно функционально полной, если она содержит хотя бы одну нелинейную и хотя бы одну немонотонную булеву функцию. Примерами ослабленных ФПСБФ могут служить следующие системы: { Λ,Å}, { Λ,~}, { V, Å}, {V,~}, {®} Логические элементы, реализующие логические функции функционально полного набора, образуют функционально полный набор логических элементов, с помощью которых можно построить любую логическую схему. Базис может быть избыточным и минимальным. Минимальный базис – такой, что удаление одной (любой) функции превращает систему ФАЛ в неполную. Иначе говоря, функционально полный базис – это набор операций алгебры логики (и соответствующих им элементов), позволяющих построить любую функцию алгебры логики. Функционально полным базисом является базис И, ИЛИ, НЕ. В то же время он функционально избыточен. Удаление из него элемента И или ИЛИ превращает его в минимальный базис. Для примера рассмотрим базис, образованный, например, элементами И и НЕ. В этом базисе реализуем функцию ИЛИ, тем самым докажем функциональную полноту выбранного базиса (рис.14).
Минимизация ФАЛ При проектировании цифровых автоматов широко используются методы минимизации булевых функций, позволяющие получать экономичные схемы. Общая задача минимизации булевых функций может быть сформулирована следующим образом: найти аналитическое выражение заданной булевой функции в форме, содержащей минимально возможное число букв. Следует отметить, что в общей постановке данная задача пока не решена, однако достаточно хорошо исследована в классе дизъюнктивно-конъюнктивных форм. Минимальной дизъюнктивной нормальной формой (МДНФ) булевой функции называется ДНФ, содержащая наименьшее число букв (по отношению ко всем другим ДНФ, представляющим заданную булеву функцию). Булева функция g(x1,...,xn) называется импликантой булевой функции f(x1,...,xn), если для любого набора переменных, на котором g=1, справедливо f=1. Таблица 12
Импликанта g булевой функции f, являющаяся элементарной конъюнкцией, называется простой, если никакая часть импликанты g не является импликантой функции f. Из примера видно, что импликанты g3 = x1x2 и g5 = x2x3 являются простыми импликантами функции f. Импликанты g1, g2, g4, g6 не являются простыми, так как их части являются импликантами функции f, например g1 является частью g3. Приведем без доказательства два утверждения, полезные при получении минимальной ДНФ. 1. Дизъюнкция любого числа импликант булевой функции f также является импликантой этой функции. 2. Любая булева функция f эквивалентна дизъюнкции всех своих простых импликант. Такая форма представления булевой функции называется сокращенной ДНФ. Перебор всех возможных импликант для булевой функции f из рассмотренного примера дает возможность убедиться, что простых импликант всего две: g3 и g5. Следовательно, сокращенная ДНФ функции f имеет вид f= g3 + g5 = x1x2 + x2x3. Как видно из табл. 12, импликанты g3, g5 в совокупности покрывают своими единицами все единицы функции f. Получение сокращенных ДНФ является первым этапом отыскания минимальных форм булевых функций. Как уже отмечалось, в сокращенную ДНФ входят все простые импликанты булевой функции. Иногда из сокращенной ДНФ можно убрать одну или несколько простых импликант, удаление которых не приводит к изменению значений функции на всевозможных значениях ее переменных. Такие простые импликанты назовем лишними. Сокращенная ДНФ булевой функции называется тупиковой, если в ней отсутствуют лишние простые импликанты. Исключение лишних простых импликант из сокращенной ДНФ булевой функции не является однозначным процессом, то есть булева функция может иметь несколько тупиковых ДНФ. Тупиковые ДНФ булевой функции f, содержащие минимальное число букв, являются минимальными (МДНФ). МДНФ тоже может быть несколько. Минимизировать функции, то есть находить наиболее простое выражение для исходной функции, можно различными методами. Все они практически различаются лишь на первом этапе - этапе получения сокращенной ДНФ. Следует отметить, что, к сожалению, поиск МДНФ всегда связан с некоторым перебором решений. Рассмотрим некоторые из них.
Метод Квайна Теорема Квайна. Для получения минимальной формы логической функции необходимо в СДНФ произвести все возможные склеивания и поглощения, так чтобы в результате была получена сокращенная ДНФ. Сокращенная ДНФ в общем случае может содержать лишние простые импликанты, которые необходимо выявить на втором этапе минимизации. На первом этапе выполняется переход от функции, заданной в форме СДНФ, к сокращенной ДНФ. Это основано на использовании следующих соотношений: 1) соотношение неполного склеивания
2) соотношение поглощения
Справедливость обоих соотношений легко проверяется. Суть метода заключается в последовательном выполнении всех возможных склеиваний и затем всех поглощений, что приводит к сокращенной ДНФ. Метод применим к совершенной ДНФ. Из соотношения поглощения следует, что произвольное элементарное произведение поглощается любой его частью. Для доказательства достаточно показать, что произвольная простая импликанта р = xi1xi2... xin может быть получена. В самом деле, применяя к р операцию развертывания (обратную операции склеивания)
по всем недостающим переменным xik,..., xim исходной функции f, получаем совокупность S конституент единицы. При склеивании всех конституент из S получим импликанту р. Последнее очевидно, поскольку операция склеивания обратна операции развертывания. Множество S конституент обязательно присутствует в совершенной ДНФ функции f, поскольку р - ее импликанта. В результате выполнения склеивания получается конъюнкция n-1 ранга, а конъюнкции Склеивание и поглощение выполняются до тех пор, пока имеются члены, не участвовавшие в попарном сравнении. Термы, подвергшиеся операции склеивания, отмечаются. Неотмеченные термы представляют собой простые импликанты и включаются в сокращенную ДНФ. Все отмеченные конъюнкции ранга n-1 подвергаются вновь операции склеивания до получения термов n-2 ранга и так далее до тех пор, пока количество неотмеченных конъюнкций больше 2. В результате выполнения первого этапа получена сокращенная ДНФ. Полученное логическое выражение не всегда оказывается минимальным. На втором этапе переходят от сокращенной ДНФ к тупиковым ДНФ и среди них выбирают МДНФ. Для формирования тупиковых ДНФ строится импликантная таблица (матрица), строки которой отмечаются простыми импликантами сокращенной ДНФ, а столбцы − конституентами единицы исходной СДНФ. В строке напротив каждой простой импликанты ставится метка под теми наборами (конституентами единицы), на которых она принимает значение 1. Соответствующие конституенты поглощаются (покрываются) данной простой импликантой. Из общего числа простых импликант необходимо отобрать их минимальное число, исключив лишние. Формирование тупиковых форм и выбор минимального покрытия начинается с выявления обязательных простых импликант, то есть таких, которые (и только они) покрывают некоторый исходный набор. Рассмотрим пример минимизации методом Квайна логической функции:
1 2 3 4 5 Выполним операцию склеивания:
3 – 5 (x2) x1x3 3 4 – 5 (x3) x1x2 4 В результате выполнения первого шага склеивания получаем четыре новые конъюнкции, простых импликант не выявлено. Полученные конъюнкции более не склеиваются и образуют сокращенную ДНФ.
Для выявления обязательных простых импликант и формирования на их основе минимального покрытия строится импликантная таблица (табл. 13). В строках импликантной таблицы записываются простые импликанты, а в столбцах − конституенты единицы. Звездочка ставится, если простая импли-канта покрывает конституенту. Таблица 13
Простые импликанты
Метод Блейка - Порецкого Метод позволяет получать сокращенную ДНФ булевой функции f из ее произвольной ДНФ. Базируется на применении формулы обобщенного склеивания:
справедливость которой легко доказать. Действительно,
Следовательно,
В основу метода положено следующее утверждение: если в произвольной ДНФ булевой функции f произвести все возможные oбобщенные склеивания, а затем выполнить все поглощения, то в результате получится сокращенная ДНФ функции f. Рассмотрим пример. Пусть булева функция f задана произвольной ДНФ.
Необходимо, используя метод Блейка – Порецкого, получить сокращенную ДНФ функции f. Проводим обобщенные склеивания. Легко видеть, что первый и второй элемент исходной ДНФ допускают обобщенное склеивание по переменной х1. В результате склеивания получим:
Первый и третий элемент исходной ДНФ допускают обобщенное склеивание как по переменной х1, так и по х2. После склеивания по x1 имеем:
После склеивания по x2 имеем:
Второй и третий элемент ДНФ допускают обобщенное склеивание по переменной х2. После склеивания получаем:
Выполнив последнее обобщенное склеивание, приходим к ДНФ:
Попытки дальнейшего применения операции обобщенного склеивания и поглощения не дают результата. Следовательно, получена сокращенная ДНФ функции f. Далее задача поиска минимальной ДНФ решается с помощью импликантной матрицы точно так же, как в методе Квайна.
Метод минимизирующих карт Карно (Вейча) При минимизации логической функции от небольшого числа переменных удобным является графический метод представления функции с помощью диаграмм (карт) Вейча и их разновидности - Карно. Карта Вейча представляет собой развертку n-мерного куба на плоскости. При этом вершины куба представляются клетками карты, каждой из которых поставлена в соответствие конститутиента единицы или нуля. Переменные, обозначающие клетки диаграммы, расставляются таким образом, чтобы наборы, записанные в двух смежных клетках, имели кодовое расстояние, равное единице. Поскольку такие наборы располагаются в смежных клетках, они получили название соседних наборов. В клетку карты, соответствующую конституенте единицы, заносится 1, иначе − 0. Таким образом, для минимизации функции она должна быть представлена в форме СДНФ. Минимизация булевой функции с использованием карт в дизъюнктивной (конъюнктивной) форме заключается в объединении единичных (нулевых) клеток в контуры, каждому такому контуру соответствует простая импликанта. Можно сформулировать следующие правила минимизации: § количество клеток карты в одном контуре должно быть равно 2n; § для контура, содержащего 2n клеток, должно быть n осей симметрии; § количество контуров должно быть минимально; § число единиц в контуре должно быть максимально; § контуры могут пересекаться, то есть некоторая клетка может входить в несколько контуров.
На рис. 15 показана заполненная карта Вейча, соответствующая функции fСДНФ. На карте обозначены четыре контура, каждый из которых содержит по две клетки. Контур 2 можно считать лишним, так как он покрывает клетки, уже покрытые двумя другими контурами (1 и 3). Аналогично можно считать лишним контур 3 (покрывается контурами 2 и 4). Здесь возможны несколько тупиковых форм ФАЛ. Таким образом, по данной карте может быть получена одна из тупиковых форм: Если функция задана в форме ДНФ, то необязательно ее приводить к форме СДНФ, что является одним из преимуществ карты Вейча. Для этого рассматривается каждый дизъюнктивный член функции в отдельности, и в соответствующие ему клетки карты заносятся единицы.
Рассмотрим сказанное на примере функции
Первому члену ДНФ поставлены в соответствие четыре клетки карты, второму – две клетки, третьему и четвертому − по одной клетке соответственно (рис.16). Далее объединение единиц в контуры и выбор их минимального числа осуществляются рассмотренным выше методом.
Если выбраны самые большие контуры и использовано по возможности меньшее их число, то будет получена самая простая дизъюнктивная нормальная форма. Дальнейшее упрощение можно получить за счет выполнения скобочных преобразований. Выражению с меньшим числом вхождений букв соответствует схема, имеющая меньшее число входов элементов, так что упрощение функций ведет к упрощению реализующих их схем.
Принимая во внимание клетки карт, не содержащие единиц, и поступая с ними так же, как мы поступали с клетками, содержащими единицы, можно получать конъюнктивные нормальные формы (рис. 17).
Если логическая функция задана таблицей истинности, то более удобной для графического представления функции является карта Карно. В отличие от карты Вейча в карте Карно строки и столбцы закодированы r-разрядным кодом Грея. Код Грея – двоичный код, в котором рядом стоящие коды – соседние (их кодовое расстояние равно единице). В карте Карно каждой клетке соответствует код, состоящий из кода строки и кода столбца (рис. 18). На рис. 19 показано соответствие клеток карты Карно и строк таблицы истинности. При этом в карте рис. 19,б показаны координаты единичных и нулевых значений функции, а в карте рис. 19,в показано соответствие строк таблицы истинности и ячеек карты.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 1415; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.96 (0.01 с.) |

 ,
, Перечислим предполные классы булевых функций.
Перечислим предполные классы булевых функций. .
.
 она принимает противоположные значения
она принимает противоположные значения  .
.
 .
.

 , где
, где  и
и  - две конъюнкции, а F - любое элементарное произведение;
- две конъюнкции, а F - любое элементарное произведение; .
.



 fСДНФ= V (1,2,5,6,7)=x1x2x3+ x1x2x3+ x1x2x3+ x1x2x3+ x1x2x3.
fСДНФ= V (1,2,5,6,7)=x1x2x3+ x1x2x3+ x1x2x3+ x1x2x3+ x1x2x3. 1 – 3 (x1) x2x3 1
1 – 3 (x1) x2x3 1 fсокр СДНФ=x2x3+ x2x3+ x1x3+ x1x2 .
fсокр СДНФ=x2x3+ x2x3+ x1x3+ x1x2 .



 являются обязательными, так как только они покрывают конституенты
являются обязательными, так как только они покрывают конституенты  и включаются в минимальное покрытие. Остается одна непокрытая конституента x1x2x3, которая может быть покрыта одной из двух оставшихся простых импликант. Это приводит к получению двух тупиковых форм:
и включаются в минимальное покрытие. Остается одна непокрытая конституента x1x2x3, которая может быть покрыта одной из двух оставшихся простых импликант. Это приводит к получению двух тупиковых форм:

 ,
,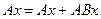 ,
,  .
.





 После выполнения поглощений получаем:
После выполнения поглощений получаем:




 x1
x1


 1
1
 1
1
 1
1

 1
1
 Контуры
1 2 3 4
Контуры
1 2 3 4








 x1
x1








 x1
x1
 0
0
 01
01






