
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Перевод чисел из одной системы счисления в другуюСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Так как числа, участвующие в операциях, могут быть представлены в различных позиционных системах счисления, то для выполнения действий над ними требуется привести их к одной системе счисления. Необходимо отметить, что целая и дробная части числа переводятся отдельно. Следовательно, все методы перевода чисел можно подразделить на две группы: перевода целых и дробных чисел. Перевод целых чисел Метод подбора степеней основания. В соответствии с (2) целые числа в системах счисления с основаниями r1 и r2 могут быть представлены: n k A r1 = i=0 j=0 В общем случае перевод числа из системы счисления с основанием r1 в систему счисления с основанием r2 можно представить как задачу определения коэффициентов bi нового ряда, изображающего число в системе счисления с основанием r2. Основная трудность в выборе максимальной степени основания r2, которая еще содержится в числе Ar1. Все действия должны выполняться по правилам r1-арифметики (то есть исходной системы счисления). После нахождения максимальной степени и соответствующего ей коэффициента необходимо найти коэффициенты для всех остальных (младших) степеней. Пример: A10=37, A2=? 37=1·25 + 0 ·24 + 0 ·23 + 1·22 + 0 ·21 + 1·20=100101. Нечетным двоичным числом 100101 является число, содержащее единицу в младшем разряде. Метод деления на основание системы счисления. На основании (1) число Ar1 в системе счисления с основанием r2 запишется в виде Ar2 = an· r2n + an-1 ·r2n-1 +... + a1· r21 + a0·r0. Переписав это выражение по схеме Горнера, получим: Ar2 = (...(an r2 + an-1) r2 +... + a1) r2 + a0. Разделив правую часть на r2, получим первый остаток a0 и целую часть (...(an r2 + an-1) r2 +... + a1). Разделив целую часть на r2, получим остаток a1 и новую целую часть. Выполнив деление n+1 раз, получим последнее целое частное an < r2, являющееся старшей цифрой числа. Пример: А10 = 37, A2 =?, А5=?
Перевод правильных дробей Метод подбора величин, обратных степеням основания A10 =0,716 А2 =0,1011...
Количество разрядов после запятой зависит от точности, с которой требуется представить число. Метод умножения на основание r2 новой системы счисления. Из выражения (1) дробное число Ar1 в системе счисления с основанием r2 запишется в виде Ar2 = a-1 r2-1 +... + a-n r2-n. Переписав это выражение по схеме Горнера, получим: Ar2 = r2-1 (a-1 + r2-1 (a-2 +... + a-n r2-1)...). Умножив правую часть на r2, получим новую неправильную дробь, целая часть которой есть a-1 (старшая цифра числа Ar2). Продолжим процесс умножения дробной части на r2 n-1 раз, получим цифры a-2, a-3,... числа Ar2. Процесс умножения может быть прекращен, если во всех разрядах после очередного умножения получены нули либо достигнута требуемая точность. Пример: A10=0,673, A2=?, A16=?
Для перевода неправильных дробей отдельно выделяется целая и дробная части числа и с использованием соответствующих методов выполняется их перевод. Результаты записываются в виде новой неправильной дроби.
Перевод чисел из одной системы счисления в другую, основание которой кратно степени 2 К таким системам относятся двоичная, четверичная, восьмеричная и т.д. системы счисления. A8 = Ограничимся тремя восьмеричными разрядами, придавая i значения 0,1,2.
+ + При переводе числа из двоичной системы счисления в восьмеричную необходимо разделить его разряды на триады, начиная с младших разрядов, и каждую триаду заменить восьмеричной цифрой.
100 101 = А2 2 5 = А16 Кодирование чисел Кодирование знака числа. Кодирование чисел позволяет заменить операцию арифметического вычитания операцией алгебраического сложения с помощью двоичного сумматора. Для кодирования знака числа используется специальный двоичный разряд, называемый знаковым. При этом знак плюс кодируется двоичной цифрой 0, а минус – цифрой 1 (для системы счисления с основанием r – цифрой r-1). Для машинного представления отрицательных чисел используют три основных вида кодов: прямой, обратный и дополнительный. Общая схема кода числа: код знака. код числа. Прямой код числа. При этом способе кодирования чисел кодируется только знак числа, а значащая часть остается без изменения.
Пример: A=+0,1101 A= - 0,1101 [A]пр=0,1101 [A]пр=1,1101
Пример: A = + 1101 A = - 1101 [A]пр=0.1101 [A]пр=1.1101 Диапазон изменения машинных изображений для прямого кода лежит в пределах: -(1-2-n) Недостатком прямого кода является сложность выполнения операции сложения чисел с разными знаками. Для арифметических операций над числами в прямом коде используется сумматор прямого кода. В этом сумматоре отсутствует цепь поразрядного переноса между старшим значащим и знаковым разрядами, то есть на этом сумматоре невозможно выполнение операции алгебраического сложения. Дополнительный код числа. Число А' называется дополнением к числу А, если выполняется соотношение: А + А¢ = rn для целых чисел или А + А'=r0 для дробных чисел, где n – количество цифр в записи числа A. Пример: A10 =378 n=3 A10' =103 – А10=1000 - 378=622 621 - все разряды дополняются до младшей цифры системы счисления
n=4 А2 =1011, Замена операции вычитания операцией сложения. В ЭВМ достаточно сложно выполнить операцию вычитания (А-В). Для этого требуется: 1) сравнить числа и выявить наибольшее из них по абсолютной величине; 2) наибольшее число разместить на входах вычитающего устройства; 3) выполнить операцию вычитания; 4) присвоить значению разности знак наибольшего по абсолютной величи- не числа. Для сложения чисел в дополнительных кодах требуется сумматор и неважно, какие слагаемые подаются на его входы А или В. Пусть необходимо сложить А = 487 А = 487 В = -348 В = 652 А-В = 139 А-В = 1 139 А + (103 – В) = А-В+103 (103 игнорируется). А = 348 А = 348 В = -487 В = 513 А-В = -139 А-В = 861 Дополнительный код отрицательных чисел является математическим дополнением абсолютной величины числа до основания r системы счисления для дробных чисел и до rn для целых чисел.
где Положительные числа в дополнительном коде не меняют своего изображения. Правило преобразования числа в дополнительный код можно записать:
Рассмотрим несколько примеров сложения чисел в дополнительных кодах. А= 0,1001 [A]доп = 0,1001 А= - 0,1001 [A]доп = 1,0111 В= - 0,0100 [B]доп = 1,1100 В= 0,0100 [B]доп = 0,0100 10,0101 1,1011 Теорема. Сумма дополнительных кодов чисел есть дополнительный код результата. Доказательство теоремы приведено в [1]. Теорема справедлива для всех случаев, в которых не возникает переполнения разрядной сетки, что позволяет складывать машинные представления чисел по правилам двоичной арифметики, не разделяя знаковую и значащую части числа. Для выполнения арифметических операций над числами в дополнительном коде используется двоичный сумматор дополнительного кода, характерной особенностью которого является наличие поразрядного переноса из старшего значащего в знаковый разряд. Обратный код числа. Обратный код двоичного числа является инверсным изображением числа, в котором все разряды исходного числа принимают инверсное (обратное) значение. Правила преобразования чисел в обратный код аналитически можно определить следующим образом:
Выполнение арифметических операций над числами в обратном коде осуществляется на сумматоре обратного кода. Этот код имеет несущественный недостаток: требует наличия в сумматоре цепи циклического переноса из знакового разряда в младший значащий. Это может привести к увеличению времени выполнения арифметических операций. Ниже приведены несколько примеров выполнения арифметических операций над числами, записанными в обратном коде. А= 0,1001 [A]обр = 0,1001 А= - 0,1001 [A]обр = 1,0110 В= - 0,0100 [B]обр = 1,1011 В= 0,0100 [B]обр = 0,0100
0,0101 Теорема. Сумма обратных кодов чисел есть обратный код результата. Доказательство теоремы приведено в [1].
|
||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 793; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.148.130 (0.012 с.) |

 ai r1i =
ai r1i = 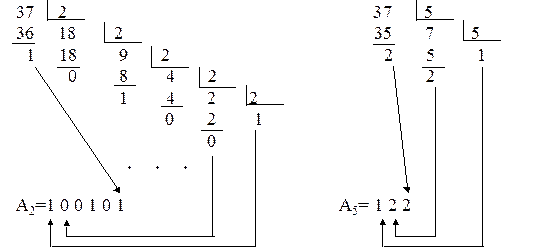


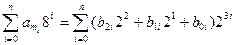 .
. + (младшая восьмеричная цифра с весом 80)
+ (младшая восьмеричная цифра с весом 80)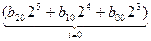 +
+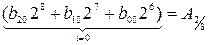
 Пример: А8 = 45 А2= 0010 0101
Пример: А8 = 45 А2= 0010 0101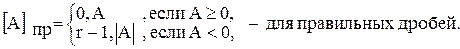
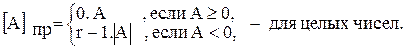
 [A]пр
[A]пр  1 - младший разряд дополняется до основания системы счисления
1 - младший разряд дополняется до основания системы счисления A2 '=24 - А=10000 - 1011 = 0101, или А2' = 0101
A2 '=24 - А=10000 - 1011 = 0101, или А2' = 0101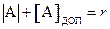 - для дробных чисел,
- для дробных чисел,  - для целых чисел,
- для целых чисел,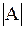 - абсолютное значение числа А, n – число цифр числа.
- абсолютное значение числа А, n – число цифр числа.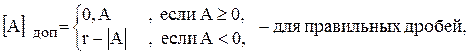
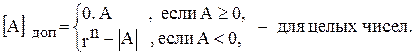
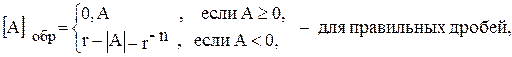 ,
,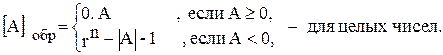 .
. 10,0100 1,1010
10,0100 1,1010 1
1


