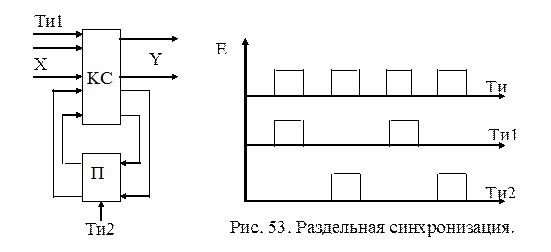Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Принцип микропрограммного управленияСодержание книги
Поиск на нашем сайте
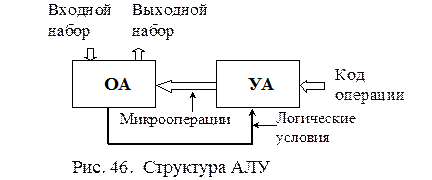
Общая структура устройства, выполняющего арифметические операции, например АЛУ, имеет структуру, представленную на рис. 46.
Элементарное действие, выполняемое за один такт автоматного времени (за один такт работы автомата), называется микрооперацией. Условия, влияющие на порядок выполнения автоматом микроопераций, называются логическими условиями. Проверка значений логических условий в каждом такте работы автомата позволяет определить группу выполняемых микроопераций. Совокупность операций, выполняемых за один такт, называется микрокомандой. Принцип, согласно которому алгоритм работы некоторого устройства описывается в перечисленных выше терминах, называется принципом микропрограммного управления. Конечный автомат, алгоритм работы которого может быть описан на основе принципа микропрограммного управления, называется микропрограммным автоматом (МПА).
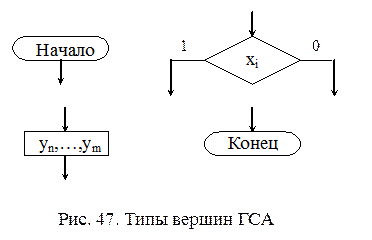
Граф-схема алгоритма Для записи микропрограмм в компактной форме используются специализированные языки. Одним из способов графического представления микропрограммы является граф-схема алгоритма (ГСА). ГСА представляет собой ориентированный связный граф. ГСА может содержать вершины четырех типов: начальную, операторную, условную и конечную (рис. 47). ГСА должна удовлетворять следующим основным требованиям: - в ГСА имеются одна начальная и одна конечная вершины; - входы и выходы вершин соединяются с помощью дуг; - каждая вершина должна лежать на одном из путей следования из начальной вершины в конечную; - один из выходов условной вершины может соединяться с ее входом; - в каждой условной вершине записывается одно из логических условий xi (допускается запись одинаковых условий в различных вершинах); - в каждой операторной вершине записывается микрокоманда (допускается пустая микрокроманда и повтор микрокоманды в различных вершинах).
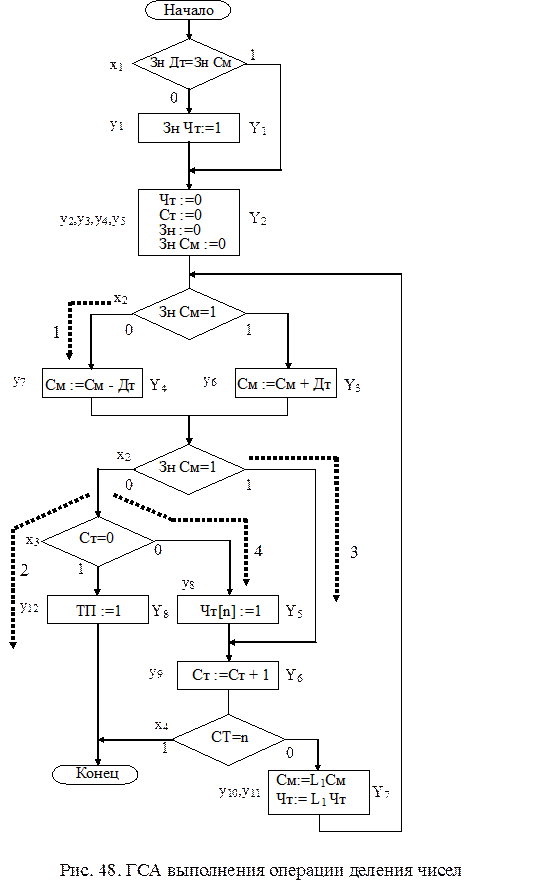
Пример синтеза МПА по ГСА МПА может быть синтезирован по ГСА, описывающей микропрограмму работы проектируемого дискретного устройства. Алгоритм синтеза МПА по ГСА состоит в следующем: - разметка ГСА метками Мили (Мура); - кодирование внутренних состояний; - построение структурной таблицы по отмеченной ГСА; - построение таблиц истинности или системы булевых функций; - построение логической схемы автомата. Как отмечалось выше, известны два класса автоматов: Мили и Мура. В качестве примера рассмотрим синтез микропрограммного автомата, управляющего операционным автоматом для выполнения операции деления чисел в дополнительных кодах. ГСА, соответствующая алгоритму деления, изображена на рис. 48. Описание алгоритма деления чисел в дополнительном коде приведено выше в соответствующем разделе. После пробного вычитания Зн См может быть равен 0, это означает, что Дм больше Дт (произошло переполнение). В этот момент счетчик тактов Ст равен 0, деление прекращается (переход в конец по стрелке 2). В последующих тактах Зн См может быть равен нулю. Это означает, что остаток Аi > Дт, но Ст уже содержит ненулевое значение, и алгоритм выполняется по стрелке 4. Если Зн См равен 1, то остаток отрицательный и деление будет выполняться в направлении стрелки 3.
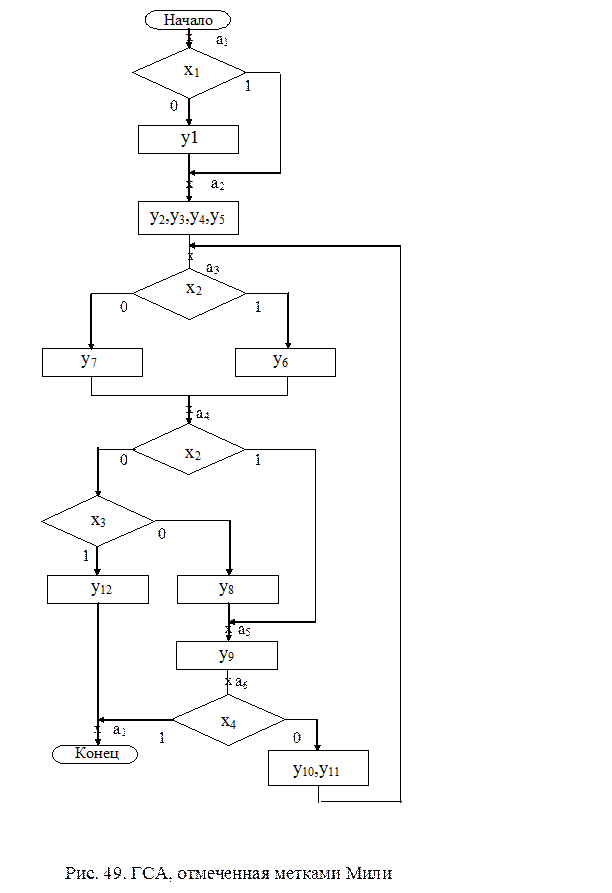
Синтез МПА Мили по ГСА Для получения графа автомата Мили исходная ГСА отмечается метками Мили. Каждой метке на ГСА ставится во взаимно однозначное соответствие состояние автомата. Алгоритм отметки ГСА метками Мили состоит в следующем: - выход начальной и вход конечной вершин отмечаются меткой а1; - входы всех вершин, следующих за операторными отмечаются метками а2,…,аm; - одной меткой может быть отмечен только один вход.
На рис. 49 приведена ГСА, отмеченная метками Мили.
Кодирование состояний автомата может быть выполнено, как и ранее, если каждому состоянию поставить в соответствие двоичный эквивалент номера состояния. Для нахождения всевозможных переходов автомата на отмеченной ГСА отыскиваются все пути вида
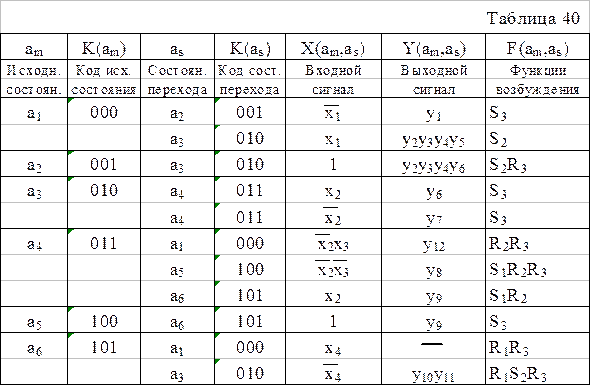
При достаточно большом числе состояний и переходов удобным является представление автомата структурной таблицей, содержащей всю необходимую для синтеза информацию. Структурная таблица может быть прямой или обратной. В прямой таблице (табл. 40) вначале записываются все переходы из со стояния а1, затем из состояния а2 и т.д. В обратной таблице сначала записываются все переходы в состояние а1, затем в а2 и т.д.. Для реализации блока памяти МПА использованы RS-триггеры. В последнем столбце отмечены те функции возбуждения, которые приводят к изменению содержимого каждого из элементов памяти на соответствующем пере ходе. В таблице в столбце F(amas) приведены функции переключения элементов памяти. Для построения схемы, реализующей синтезируемый МПА, удобно результаты, приведенные в структурной таблице (табл. 40), представить в виде таблицы истинности (табл. 41).
Таблица 41.
Для примера реализации логической схемы синтезируемого МПА рассмотрим реализацию функций y1 y2 и S2 R2 (рис. 50). Синхронизация автоматов Нарушение функционирования автомата может быть вызвано явлениями, получившими название гонки и риск сбоя. Гонки возникают из-за неодновременного срабатывания элементов памяти автомата вследствие разброса во времени переключения триггеров, а так же различия по времени поступления сигналов на их входы. Например, пусть под действием некоторого входного сигнала X(amas) с кодом 00 автомат должен перейти из состояния am с кодом 101 в состояние as с кодом 110 (рис. 51). Если второй триггер изменит свое значение − переключится из 0 в 1 ранее, чем третий переключится из 1 в 0, то автомат перейдет в промежуточное состояние 111. Иначе, если третий триггер сработает ранее второго, − то в промежуточное состояние 100.
Существует два основных подхода к устранению гонок: программный и аппаратный. Программный (алгоритмический) подход основан на соседнем кодировании состояний. При соседнем кодировании состояния автомата из множества A={a1,…,am} кодируются таким образом, что на любом переходе изменяет свое состояние не более чем один элемент памяти. Однако соседнее кодирование возможно выполнить не для всех автоматов. Аппаратный подход основан на использовании двух ступеней памяти (рис. 52). Первая ступень памяти построена на триггерах T1 ’,…,Tr ’, вторая − на триггерах T1 ”,…,Tr ”. Информация в триггеры первого уровня T1 ’,…,Tr ’ записывается по тактовому сигналу Ти, а в триггеры второго уровня T1 ”,…,Tr ” − по сигналу Ти, следующему непосредственно за Ти.
 Если комбинационная схема автомата построена из синхронизируемых элементов, то гонки также устраняются путем разделения синхронизации памяти и комбинационной схемы (рис. 53). В этом случае двойная память не требуется. Если комбинационная схема автомата построена из синхронизируемых элементов, то гонки также устраняются путем разделения синхронизации памяти и комбинационной схемы (рис. 53). В этом случае двойная память не требуется.
Риск сбоя. Наличие некритических ”состязаний” не нарушает правил перехода в автомате, но создает возможность возникновения риска сбоя. Риск сбоя заключается в том, что при переходе в некоторое промежуточное состояние (реально существующее в алгоритме) может быть выработан кратковременный ложный выходной сигнал. Например, в автомате Мура при переходе из
Хотя длительность ложного сигнала yk достаточно мала, его возникновение может привести к непредсказуемым последствиям в работе устройства, которым управляет автомат. Для устранения риска сбоя можно воспользоваться следующими методами: - выходы автомата, на которых может возникнуть риск сбоя, соединяются через конденсатор небольшой емкости с нулевым выходом источника питания (рис. 55.); - буферизация выходных сигналов;
- синхронизация выходных сигналов автомата. При этом комбинационная схема имеет дополнительный вход синхронизации Cs, поступающий с задержкой относительно основного синхросигнала. Сигналы на выходах автомата появляются только при наличии этого сигнала. Сигнал можно сформировать, как показано на рис. 56. Схема может быть построена, например, из инверторов (их должно быть четное число). Данный подход позволяет устранить риск сбоя только для автомата Мура, так как синхронизация позволяет формировать выходные сигналы после окончания переходных процессов.
Литература
1. Савельев А.Я. Прикладная теория цифровых автоматов: Учеб. для вузов по спец. ЭВМ. –М.: Высш. шк., 1987. 2. Поснов Н.Н. Арифметика вычислительных машин в упражнениях и задачах: системы счисления, коды. –Мн.: Университетское, 1984. 3. Морозевич А.Н. Дмитриев А.Н. и др. МикроЭВМ, микропроцессоры и основы программирования. –Мн.: Выш. шк., 1990 4. Акушинский И.Я., Юдицкий Д.И. Машинная арифметика в остаточных классах. –М.: Сов. радио, 1968. 5. Питерсон У., Уэлдон Э. Коды, исправляющие ошибки. Пер. с англ. –М.: Мир, 1976.
Содержание Введение. 3 Арифметические основы вычислительной техники. 3 Системы счисления. 3 Двоичная система счисления. 4 Восьмеричная система счисления. 5 Шестнадцатеричная система счисления. 6 Критерии выбора системы счисления. 6 Перевод чисел из одной системы счисления в другую.. 9 Перевод целых чисел. 9 Перевод правильных дробей. 10 Перевод чисел из одной системы счисления в другую, основание которой кратно степени 2. 11 Кодирование чисел. 12 Переполнение разрядной сетки. 14 Модифицированные коды.. 15 Машинные формы представления чисел. 16 Погрешность выполнения арифметических операций. 18 Округление. 18 Нормализация чисел. 19 Последовательное и параллельное сложение чисел. 19 Сложение чисел с плавающей запятой. 21 Машинные методы умножения чисел в прямых кодах. 22 Ускорение операции умножения. 25 Умножение с хранением переносов. 25 Умножение на два разряда множителя одновременно. 26 Умножение на четыре разряда одновременно. 28 Умножение в дополнительных кодах. 29 Умножение на два разряда множителя в дополнительных кодах. 34 Матричные методы умножения. 36 Машинные методы деления. 37 Деление чисел в прямых кодах. 38 Деление чисел в дополнительных кодах. 40 Методы ускорения деления. 41 Двоично-десятичные коды.. 41 Суммирование чисел с одинаковыми знаками в BCD-коде. 43 Суммирование чисел с разными знаками в BCD-коде. 44 BCD-коды с избытком 3. 46 BCD-код с избытком 6 для одного из слагаемых. 47 Система счисления в остаточных классах (СОК) 48 Представление отрицательных чисел в СОК.. 51 Контроль работы цифрового автомата. 52 Некоторые понятия теории кодирования. 53 Обнаружение и исправление одиночных ошибок путем использования дополнительных разрядов. 54 Коды Хемминга. 55 Логические основы вычислительной техники. 57 Двоичные переменные и булевы функции. 57 Способы задания булевых функций. 58 Основные понятия алгебры логики. 59 Основные законы алгебры логики. 62 Формы представления функций алгебры логики. 63 Системы функций алгебры логики. 65 Минимизация ФАЛ.. 69 Метод Квайна. 71 Метод Блейка - Порецкого. 73 Метод минимизирующих карт Карно (Вейча) 74 Минимизация конъюнктивных нормальных форм. 76 Минимизация не полностью определенных ФАЛ.. 77 Кубическое задание функций алгебры логики. 78 Метод Квайна −Мак-Класки. 81 Алгоритм извлечения (Рота) 83 Минимизация ФАЛ методом преобразования логических выражений. 92 Применение правил и законов алгебры логики к синтезу некоторых цифровых устройств. 92 Синтез одноразрядного полного комбинационного сумматора. 92 Синтез одноразрядного комбинационного полусумматора. 93 Синтез одноразрядного полного комбинационного сумматора на двух полусумматорах. 94 Синтез одноразрядного комбинационного вычитателя. 95 Объединенная схема одноразрядного комбинационного сумматора-вычитателя 95 Триггер со счетным входом как полный одноразрядный сумматор. 96 Введение в теорию конечных автоматов. 97 Основные понятия теории автоматов. 97 Способы задания автоматов. 99 Структурный автомат. 101 Память автомата. 101 Канонический метод структурного синтеза автоматов. 104 Принцип микропрограммного управления. 109 Граф-схема алгоритма. 109 Пример синтеза МПА по ГСА.. 110 Синтез МПА Мили по ГСА.. 110 Синхронизация автоматов. 115 Литература. 118
Св. план 2004, поз.59
Учебное издание
Луцик Юрий Александрович, Лукьянова Ирина Викторовна
АРИФМЕТИЧЕСКИЕ И ЛОГИЧЕСКИЕ ОСНОВЫ ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ
Учебное пособие по курсу «Арифметические и логические основы вычислительной техники»
Редактор Т.А. Лейко Корректор Е.Н. Батурчик Компьютерная верстка Подписано в печать..2004. Формат 60х84 1/16. Бумага офсетная. Гарнитура Times New Roman. Печать ризографическая. Усл. печ. л. Уч.- изд. л. 6,0. Тираж экз. Заказ
Издатель и полиграфическое исполнение: Учреждение образования «Белорусский государственный университет информатики и радиоэлектроники» Лицензия ЛП № 156 от 05.02. 2001. Лицензия ЛВ № 509 от 03.08. 2001. 220013, Минск, П.Бровки, 6
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 606; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.96 (0.01 с.) |

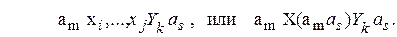
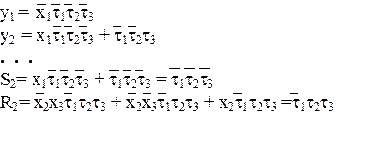



 Если в течение первого полупериода (Ти) между триггерами первой ступени и возникают ”состязания”, то они все равно не изменяют состояния триггеров второй ступени, поскольку отсутствует синхросигнал Ти. Затем, с
Если в течение первого полупериода (Ти) между триггерами первой ступени и возникают ”состязания”, то они все равно не изменяют состояния триггеров второй ступени, поскольку отсутствует синхросигнал Ти. Затем, с  приходом синхроимпульса Ти, изменяют свое состояние
приходом синхроимпульса Ти, изменяют свое состояние