
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Суммирование чисел с одинаковыми знаками в BCD-кодеСодержание книги
Поиск на нашем сайте
При выполнении операций над отмеченными кодами возможны следующие особенности: § наличие разрешенных и запрещенных комбинаций, свидетельствующих о правильности результата или необходимости его коррекции; § при сложении тетрад возможен потетрадный (16 единиц), а не поразрядный (10 единиц) перенос, что также требует корректировки результата. При сложении чисел в BCD-коде возможны три случая: 1) (a + b) ≤ 9. В этом случае если действия выполняются по правилам двоичной арифметики, то величина получаемой суммы не превышает девяти и коррекция результата не требуется. 5 0101 + 30011 8 1000 2) 10 ≤ (a + b) ≤ 15. Если результат сложения двух чисел попадает в данный диапазон чисел, то возможны два случая результирующей тетрады. 5 0101 9 1001 + 60110 + 40100 11 1011 13 1101 В этом случае в тетраде накопилось более девяти единиц и должен быть выполнен десятичный перенос. Перенос единицы в старший разряд выполняется принудительно логической схемой. Условием для формирования единицы переноса является возникновение запрещенной комбинации (наличие единицы в разрядах с весом 8 и 4 или 8 и 2). Однако тетраду надо освободить от десяти избыточных единиц. Это тоже делается принудительно добавлением 0110 (шестерки), что приводит к возникновению шестнадцатеричного переноса. Этот перенос игнорируется. Схема формирования принудительного переноса приведена на рис.11. 3) (a + b) ≥ 16. Здесь в процессе суммирования возникает шестнадцатеричный перенос, в результате которого тетраду покидают вместе с десятком и те шесть единиц, которые принадлежат тетраде. Чтобы восстановить верное значение этой тетрады, необходимо к ней добавить 0110 (шесть).
8 1000 + 91001 17 1 0001 0110 Коррекция(+6) 0111
Таким образом, из сказанного выше можно сформулировать следующие правила потетрадного сложения чисел в BCD-кодах. § Если при потетрадном сложении перенос в соседнюю старшую тетраду не возникает, то результат суммирования не требует коррекции. § Коррекция результата потетрадного сложения путем добавления поправки 0110 требуется в случае, если возникает: а) потетрадный перенос в старшую тетраду; б) запрещенная комбинация. Устройство, которое работает по сформулированным выше правилам, называется одноразрядным двоично-десятичным сумматором (рис.12).
Пример: сложить числа А=169 и В=378 в BCD-коде A = 169 A = 0.0001 0110 1001 + B = 378 + B = 0.0011 0111 1000 A + B = 547 A + B = 0.0101 1110 0001
0.0101 0100 0111
Суммирование чисел с разными знаками в BCD-коде Отрицательные BCD-коды должны представляться в прямом, обратном или дополнительном кодах. Особенностью BCD-кодов является то, что инверсия тетрады означает дополнение до 15, а для соответствующей десятичной цифры до 9. Следовательно, необходимо убрать разницу. Один из приемов формирования обратного BCD-кода состоит в добавлении во все тетрады отрицательного числа 0110, затем их инверсии.
При сложении чисел с разными знаками возможны следующие случаи. 1) a - b ≥ 0 a = 7 0. 0111 [ a ]обр b= -31. 1100 [ b ]обр 4 10. 0011
0. 0100 При образовании инверсии отрицательной тетрады в нее добавляются 15 единиц. Эти 15 единиц находятся и в сумме. Но благодаря шестнадцатеричному переносу из тетрады уходит 16 единиц (15+1 − эта единица восстанавливается добавлением по цепи циклического переноса). 2) a - b < 0 a = 3 0. 0011 [ a ]обр b = -71. 1000 [ b ]обр -4 1. 1011 0. 0100 Здесь, как и в предыдущем примере, в тетраде суммы пятнадцать лишних единиц. Но при переходе от инверсной формы к прямой лишние единицы уничтожаются сами собой. Это то же самое, что от значащей части суммы вычесть пятнадцать: 1011 - 1111 = 0100. Рассмотрим несколько примеров.
A = 378 0. 0011 0111 1000 – B = 1691. 1110 1001 0110 A – B = 209 10. 0010 0000 1110
0. 0010 0000 1111 Из последней тетрады нет переноса, таким образом, это соответствует заему в нее 16 единиц (вместо необходимых 10). Следовательно, из нее необходимо удалить лишние шесть единиц. Для этого в тетраду добавляется 10 - дополнение шести до шестнадцати: 0. 0010 0000 1111 1010 0. 0010 0000 1001 + 2 0 9
A–B= - 209 1. 1101 1111 0000 0110 1. 1101 1111 0110 - 0010 0000 1001 - 2 0 9 Таким образом, в тетраду производится заем, если результат: § положительный и из тетрады нет переноса; § отрицательный и из тетрады есть перенос. BCD-коды с избытком 3 Иначе говоря, это коды чисел из системы (BCD + 3). В этом коде каждая десятичная цифра ai представляется в виде двоичного эквивалента суммы ai+3. В отличие от BCD-кода код BCD+3 – самодополняющийся, но не имеющий свойства взвешенности. Применяется наиболее часто в десятичной арифметике, так как при выполнении двоичного суммирования легко выделить десятичный перенос. Возможны следующие два случая сложения чисел в BCD-коде +3: 1) a + b ≤ 9; [ (a + 3) + (b + 3) ] ≤ 15. И, следовательно, в тетраде суммы будут лишние 6 единиц. Чтобы тетрада суммы осталась тоже с избытком 3, нужно вычесть 3. 2) a + b ≥ 10; [ (a + 3) + (b + 3) ] ≥ 16. Здесь во всех случаях возникает шестнадцатеричный перенос, вместе с которым тетраду суммы покинут и шесть избыточных единиц; чтобы тетрада суммы осталась с избытком 3, надо добавить 3. Если складываются числа с разными знаками, то избыток в тетраде суммы будет равен нулю и суммирование, таким образом, сводится к правилам суммирования в BCD-коде. Пример. Выполнить сложение чисел 169 и 378 в BCD-коде +3. 0.0100 1001 1100 A = 169 0.0110 1010 1011 B = 378 0.1011 0100 0111 A + B = 547 -0011+0011+0011 0.1000 0111 1010 8 7 10 Пример. Выполнить вычитание из числа 378 числа 169 в BCD-коде +3. A = 378 0.0110 1010 1011 B = 1691.1011 0110 0011 A - B = 209 1 0.0010 0000 1110
+ 0011 -0011 -0011 0.0101 0011 1100 5 3 12 Пример. Выполнить вычитание из числа 169 числа 378 в BCD-коде +3. A = 169 0.0100 1001 1100 B = 3781.1001 0101 0100 A - B = -209 1.1101 1111 0000 -0011 -0011 +1100 1.1010 1100 0011 - 0101 0011 1100 5 3 12 Правило. Если из тетрады был перенос, надо добавить +0011, если переноса не было, – 0011 (добавить 1100), независимо от знака слагаемых и знака суммы.
|
|||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 675; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.96 (0.01 с.) |


 0110 0110
0110 0110 перенос игнорируется
перенос игнорируется
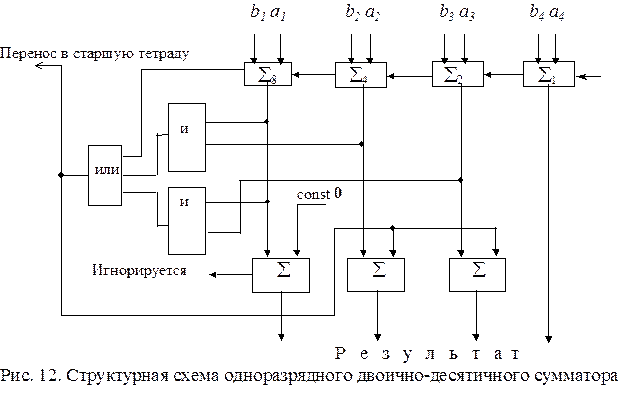

 1
1 циклический перенос 1
циклический перенос 1 A = 169 0. 0001 0110 1001
A = 169 0. 0001 0110 1001 B = 378 1. 1100 1000 0111
B = 378 1. 1100 1000 0111 циклический перенос 1
циклический перенос 1 0.0010 0000 1111
0.0010 0000 1111


