
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Применение правил и законов алгебры логики К синтезу некоторых цифровых устройствСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Синтез одноразрядного полного комбинационного сумматора Пусть имеется два числа: A=a1a2... a i-1a ia i+1... an, B=b1b2... b i-1bib i+1... bn. В зависимости от значений аргументов ai, bi, zi (перенос в i-й разряд) формируется значение булевых функций Ci, и Пi. Введем следующие обозначения. ai Þ x Ci Þ С, где Сi – значение суммы в разряде i bi Þ y Пi Þ П Пi – значение переноса из разряда i zi Þ z Таблица истинности, отражающая алгоритм работы сумматора, имеет следующий вид (табл. 23).
Таблица 23
Запись одной функции с участием другой носит название совместной минимизации. Следовательно, с учетом этого функция C будет иметь вид
Таким образом, логическая схема синтезированного одноразрядного полного комбинационного сумматора имеет следующий вид (рис. 31).
Синтез одноразрядного комбинационного полусумматора Одноразрядный полусумматор − это устройство для сложения разрядов двух чисел без учета переноса из предыдущего разряда, имеющее два входа (два суммируемые разряды) и два выхода (суммы и переноса). Таблица истинности, отражающая алгоритм работы полусумматора, имеет следующий вид (табл. 24).
Таблица 24
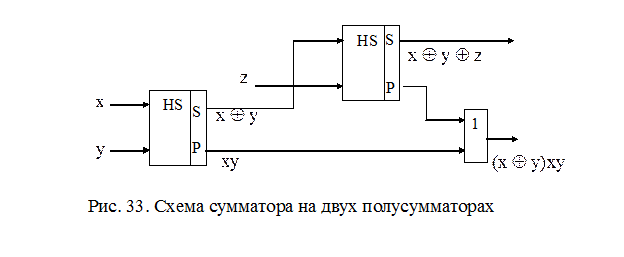
Синтез одноразрядного полного комбинационного сумматора на двух полусумматорах Согласно рассмотренному выше материалу функция суммирования для полного комбинационного сумматора имеет вид
Введем обозначение
Аналогично можно выполнить преобразование функции переноса П:
Таким образом, схема полного сумматора на двух полусумматорах будет иметь следующий вид (рис. 33).
Синтез одноразрядного комбинационного вычитателя Пусть имеется два числа: A=a1a2... a i-1a ia i+1... an, B=b1b2... b i-1bib i+1... bn. В зависимости от значений аргументов ai, bi, zi (заем из i-го разряда) формируется значение булевых функций Рi, и Зi. Введем следующие обозначения. ai Þ x Рi Þ Р, где Рi – значение разности в разряде i bi Þ y Зi Þ З Зi – значение заема в разряд i zi Þ z - заем из i-го разряда Таблица истинности, соответствующая устройству, выполняющему операцию вычитания, имеет следующий вид (табл. 25). Таблица 25
Объединенная схема одноразрядного комбинационного сумматора-вычитателя Для системы булевых функций C, P, П и З, полученных выше, может быть построена логическая схема (рис. 34) на элементах И, ИЛИ и НЕ.
Триггером называется устройство, имеющее два устойчивых состояния и способное под действием входного сигнала скачком переходить из одного устойчивого состояния в другое. Триггер – это простейший цифровой автомат с памятью и способностью хранить 1 бит информации. Триггер со счетным входом (Т-триггер) может быть рассмотрен как полный сумматор, работающий в три такта. В основе работы этого устройства лежит операция ”сумма по модулю 2”. Первый такт. 1) τ(t-1)=0 – триггер находится в исходном состоянии. 2) Т=x первое слагаемое подается на вход триггера
следовательно, после первого такта содержимое триггера будет соответствовать его входному сигналу. Второй такт. Во втором такте на вход триггера подается второе слагаемое y.
на выходе триггера формируется сумма по модулю 2 слагаемых x и y. Третий такт. В третьем такте на вход триггера поступает значение, соответствующее третьему слагаемому – z.
Из полученной функции видно, что на выходе T-триггера получена полная сумма трех слагаемых и, следовательно, триггер со счетным входом является полным сумматором, работающим в три такта. Введение в теорию конечных автоматов
Основные понятия теории автоматов Все рассмотренные выше устройства относятся к классу комбинационных схем, то есть дискретных устройств без памяти. Наряду с ними в цифровой технике широкое распространение получили последовательностные автоматы, или, иначе, комбинационные схемы, объединенные с элементами памяти. Под термином автомат можно понимать некоторое реально существующее устройство, функционирующее на основании как сигналов о состоянии внешней среды, так и внутренних сигналов о состоянии самого автомата. В этом плане ЭВМ может быть рассмотрена как цифровой автомат. Под цифровым автоматом понимается устройство, предназначенное для преобразования цифровой информации. С другой стороны, под термином автомат можно понимать математическую модель некоторого устройства. Общая теория автоматов подразделяется на две части: абстрактную и структурную теорию автоматов. Различие между ними состоит в том, что абстрактная теория абстрагируется от структуры как самого автомата, так и входных и выходных сигналов. В абстрактной теории анализируются переходы автомата под воздействием абстрактных входных слов и формируемые на этих переходах абстрактные выходные слова. В структурной теории рассматривается структура как самого автомата, так и его входных и выходных сигналов, способы построения автоматов из элементарных автоматов, способы кодирования входных и выходных сигналов, состояний автомата. В соответствии с этим принято различать две модели автоматов: структурную и абстрактную. Абстрактная модель применяется при теоретическом рассмотрении автоматов. Структурная модель служит для построения схемы автомата из логических элементов и триггеров и предназначена для выполнения функции управления. Абстрактный автомат – это математическая модель цифрового автомата, задаваемая шестикомпонентным вектором S=(A,Z,W,d,l,a1), где А={aa,…,am} – множество внутренних состояний абстрактного автомата; Z=[z1,…,zk} и W={w1,…,wl} – соответственно множества входных и выходных абстрактных слов; d - функция переходов; l - функция выходов; a1 – начальное состояние автомата. Абстрактный автомат может быть представлен как устройство с одним входом и одним выходом (рис. 35), на которые подаются абстрактные входные слова и формируются абстрактные выходные слова.
Понятие состояние автомата используется для описания систем, выходы которых зависят не только от входных сигналов, но и от предыстории, то есть информации о том, что происходило с автоматом в предыдущий интервал времени. Состояние автомата позволяет устранить время как явную переменную и выразить выходные сигналы как функцию состояний и входных сигналов. По виду функции выходов все множество автоматов можно подразделить на два класса: автоматы Мили и автоматы Мура. Автоматами Мура, или автоматами первого типа, называют автоматы, для которых абстрактное выходное слово w(t) не зависит явно от входного слова z(t), а определяется только состоянием автомата в момент времени t. Закон функционирования автомата Мура может быть описан системой уравнений:
К автоматам второго типа, или автоматам Мили, относятся автоматы, поведение которых может быть описано системой уравнений:
Следовательно, в отличие от автомата Мура для автомата Мили выходной символ w(t) зависит не только от текущего состояния, но и от входного символа. Между моделями автоматов Мили и Мура существует соответствие, позволяющее преобразовать закон функционирования одного из них в другой. Совмещенная модель автомата (С-автомат). Абстрактный С-автомат – математическая модель дискретного устройства, определяемого вектором S=(A,Z,W,U,d,l1,l2,a1), где А, Z, d и а1 определены выше, а W={w1,…,wl} и U={u1,…,ul} – выходной абстрактный алфавит автомата Мили и Мура соответственно, l1 и l2 - функции выходов. Абстрактный С-автомат может быть представлен как устройство с одним входом, на который поступают слова из входного алфавита Z, и двумя выходами (рис. 36), на которых формируются абстрактные выходные слова из выходных алфавитов W и U.
Отличие С-автомата от моделей автоматов Мили и Мура заключается в том, что он одновременно реализует две функции выходов l1 и l2, каждая из которых характерна для одной из двух моделей.
Автомат S называется конечным, если конечны множества A, Z и W, и детерминированным, если, находясь в некотором состоянии, он не может перейти более чем в одно состояние под действием одного и того же входного символа. Если в автомате выделено начальное состояние а1, то он называется инициальным. Состояние аs называется устойчивым, если для любого zkÎZ, такого что as=d(am,zk), as=d(as,zk), то есть если автомат из состояния am в перешел в состояние as под действием входного слова zk , то выйти из этого состояния он может только под действием другого входного слова. Автомат S является асинхронным, если каждое его состояние устойчиво, иначе синхронным. Автомат называется полностью определенным, если область определения функции d совпадает с множеством пар (am,zk), а функции l для автомата Мили − с множеством пар (am,zk), Мура − с множеством am. У частичного автомата функции d и l определены не для всех пар.
Способы задания автоматов Закон функционирования автоматов может быть задан в виде систем уравнений, таблиц, матриц и графов. Под законом функционирования понимается совокупность правил, описывающих переходы автомата в новое состояние и формирование выходных символов в соответствии с последовательностью входных символов. В зависимости от типа автомата при табличном задании закона функционирования автомата используются либо таблицы переходов и выходов (автомат Мили), либо совмещенная таблица переходов и выходов (автомат Мура). С помощью табл. 26 и 27 (таблицы переходов и таблицы выходов соответственно) задан закон функционирования абстрактного автомата Мили, для которого A={a1,a2,a3,a4}, Z={z1,z2,z3}, W={w1,w2,w3,w4,w5}.
Как отмечалось выше, для автомата Мура выходной символ не зависит от входного, а определяется только текущим состоянием автомата. Это позволяет для автомата Мура объединить обе таблицы (переходов и выходов) в одну совмещенную таблицу. В совмещенной таблице переходов и выходов каждый столбец отмечается состоянием am ÍА и выходным символом w(t)=l(a(t)), соответствующим этому состоянию. Другим, более наглядным способом описания закона функционирования автомата является представление его в виде графа. Граф автомата – ориентированный граф, вершины которого соответствуют состояниям, а дуги − переходам между ними. Дуга, направленная из вершины am в вершину as, соответствует переходу из состояния am в as. В начале дуги записывается входной символ zi, влияющий на переход as=d(am,zi), а символ wj записывается в конце дуги (автомат Мили) или рядом с вершиной (автомат Мура). На рис. 37 приведен граф автомата Мили, соответствующий закону функционирования, описанному выше (см. табл. 26 и 27).
Структурный автомат В отличие от абстрактного автомата структурный автомат имеет L входов и N выходов. На входы структурного автомата поступают наборы входных двоичных переменных из множества X={x1,x2,…,xL}, а на выходах формируются выходные двоичные сигналы из множества Y={y1,y2,…,yN}. Структурная модель автомата представляет собой две взаимосвязанные части: комбинационную схему и память. Комбинационная часть автомата кроме сигналов из множества Y формирует также двоичные сигналы, подаваемые на входы элементов памяти D={d1,d2,…,dr}. Эти сигналы называются функциями возбуждения элементов памяти и представляют собой код состояния перехода. Сигналы, формируемые на выходах элементов памяти T={t1,t2,…,tr}, подаются на входы комбинационной схемы наряду с входными переменными и называются переменными обратной связи. Переменные обратной связи являются кодом текущего состояния автомата. Структурная схема автомата изображена на рис. 38.
Любому переходу в абстрактном автомате из состояния am в состояние as под действием входного слова zi с формированием выходного слова wj соответствует переход в стуктурном автомате из состояния am с кодом t1,…,tr в состояние as с кодом d1,…,dr под действием набора входных сигналов x1,…,xL с формированием выходного набора y1,…,yN. Память автомата В качестве элементов памяти автомата используются простейшие схемы, предназначенные для приема, хранения и передачи одного бита информации − триггеры. Триггер имеет один или более входов и два выхода (прямой и инверсный). Выходные сигналы триггера зависят только от его состояния и изменяются только при смене состояния триггера. Таким образом, триггеры являются элементарными автоматами Мура (элементарными, так как они имеют только два устойчивых состояния). В основе любого триггера находится регенеративное кольцо из двух инверторов. Триггеры можно классифицировать по следующим признакам: 1) по способу записи информации: несинхронизируемые (асинхронные) и синхронизируемые (синхронные) триггеры. У асинхронных триггеров запись информации происходит под действием информационных сигналов, у синхронных кроме информационных на вход должны быть поданы разрешающие сигналы; 2) по способу синхронизации: синхронные триггеры со статическим управлением записью, синхронные двухступенчатые триггеры, синхронные триггеры с динамическим управлением записью; 3) по способу организации логических связей: триггеры с раздельной установкой состояния (RS-триггеры), триггеры со счетным входом (Т-триггеры), универсальные триггеры с раздельной установкой состояний (JK-триггеры), триггеры с приемом информации по одному входу (D-триггеры), комбинированные триггеры (RST-, JKRS-, DRS-триггеры и т.д.), триггеры со сложной входной логикой. Приняты следующие изображения входов триггеров: S − раздельный вход установки триггера в единичное состояние по прямому выходу; R − раздельный вход сброса триггера в нулевое состояние по прямому выходу; J и K − назначение аналогично входам S и R; D − информационный вход. Используется для приема информации, записываемой в триггер; T − счетный вход; С − вход синхронизации.
D-триггер. Принцип работы синхронного D-триггера основан на том, что сигнал на выходе после переключения равен сигналу на входе D до переключения. На рис. 39 приведена схема одноступенчатого D-триггера на элементах И-НЕ и его условное изображение.
T-триггер. Принцип работы Т-триггера основан на том, что единичный сигнал на входе изменяет содержимое триггера на противоположное. На рис.40 приведена схема Т-триггера на элементах И-НЕ и его условное изображение. В табл.29 приведена информация о работе Т-триггера. Переключение состояний выполняется по формуле t(t+1)= t(t) Å T.
RS-триггеры. Асинхронные RS-триггеры являются простейшими триггерами. Такие триггеры строятся на логических элементах: 2ИЛИ-НЕ – триггер с прямыми входами (рис. 41) или 2И-НЕ – триггер с инверсными входами. Выход каждого из логических элементов подключен к одному из входов другого элемента, что обеспечивает нахождение триггера в одном из двух устойчивых состояний.
Таблица 30
Возможны следующие режимы работы RS-триггера: S=0, R=0 – режим хранения информации (значение триггера не изменяется); S=0, R=1 – режим сброса (триггер всегда устанавливается в 0); S=1, R=0 – режим записи логической единицы (триггер устанавливается в 1); S=1, R=1 – запрещенная комбинация (значение триггера не неопределенное). JK-триггеры. Асинхронный JK-триггер строится на базе RS-триггера. JK-триггер имеет два информационных входа. Простейший JK-триггер можно получить из RS-триггера, если ввести дополнительные обратные связи с выходов триггера на входы, которые позволяют устранить неопределенность в таблице состояний. Логическая схема и условное обозначение JK-триггера приведены на рис. 42.
Возможны следующие режимы работы RS-триггера: J=0, K=0 – режим хранения информации (значение триггера не изменяется); J=0, K=1 – режим сброса (триггер всегда устанавливается в 0); J=1, K=0 – режим записи логической единицы (триггер устанавливается в 1); J=1, K=1 – режим инверсии содержимого триггера. JK-триггер является универсальным триггером. Универсальность его состоит в том, что он может выполнять функции RS-, T- и D-триггеров. Для получения D-триггера K вход соединяется со входом J через инвертор. T-триггер получается из JK-триггера путем объединения входов J и K в один, называемый T-входом. Если JK-триггер предварительно установлен в 0 и на вход не подается комбинация 11, то он работает как RS-триггер.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 647; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.96 (0.013 с.) |

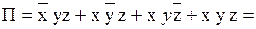

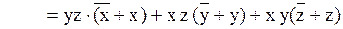 .
.
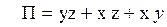 .
.

 Ü Логические нули
Ü Логические нули
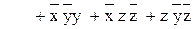 =
=
 ,
,


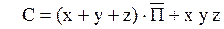 .
.
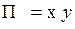

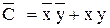 Данная схема может быть упрощена, если функция C будет записана на нулевых наборах и использована совместная минимизация.
Данная схема может быть упрощена, если функция C будет записана на нулевых наборах и использована совместная минимизация.

 .
. , тогда
, тогда .
. .
.

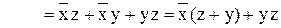 .
.
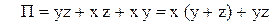 .
.
 С.
С.
 Триггер со счетным входом как полный одноразрядный сумматор
Триггер со счетным входом как полный одноразрядный сумматор ,
, ,
,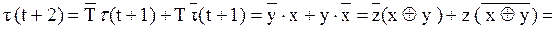
 .
.

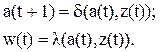
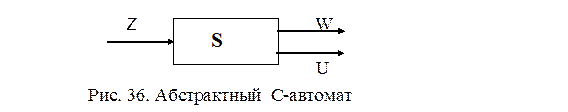
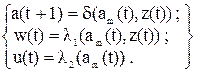
 Строки таблиц отмечены входными символами (элементы множества Z), а столбцы − состояниями (элементы множества А). Входные символы и состояния, которыми помечены строки и столбцы, относятся к моменту времени t. В табл. 26 (таблице переходов) на пересечении строки zi(t) и столбца am(t) ставится состояние as(t+1)=d(am(t),zi(t)). В табл. 27 (таблице выходов) на пересечении строки zi(t) и столбца am(t) ставится выходной символ w(t)=l(am(t),zi(t)), соответствующий переходу из состояния аm в состояние as. Таким образом, по таблицам переходов и выходов можно проследить последовательность работы автомата. Так, например, в начальный момент времени t=0 автомат, находясь в состоянии a1 (первый столбец), под действием входного символа z1 может перейти в состояние a2, при этом выходной символ не формируется; под действием входного символа z2 − в состояние a4 с формированием выходного символа w2; под действием символа z3 − в состояние a3 с формированием выходного символа w3. Далее если на вход автомата, установленного в исходное состояние аm ÍA, в моменты времени t=1,2,…,n подается некоторая последовательность букв входного алфавита (входных символов) ziÍZ, то на выходе автомата будут последовательно формироваться буквы выходного алфавита (выходные символы) wjÍW, при этом автомат будет переключаться в состояния asÍA. Следовательно, с помощью таблиц переходов и выходов можно получить выходную реакцию автомата на любое входное слово.
Строки таблиц отмечены входными символами (элементы множества Z), а столбцы − состояниями (элементы множества А). Входные символы и состояния, которыми помечены строки и столбцы, относятся к моменту времени t. В табл. 26 (таблице переходов) на пересечении строки zi(t) и столбца am(t) ставится состояние as(t+1)=d(am(t),zi(t)). В табл. 27 (таблице выходов) на пересечении строки zi(t) и столбца am(t) ставится выходной символ w(t)=l(am(t),zi(t)), соответствующий переходу из состояния аm в состояние as. Таким образом, по таблицам переходов и выходов можно проследить последовательность работы автомата. Так, например, в начальный момент времени t=0 автомат, находясь в состоянии a1 (первый столбец), под действием входного символа z1 может перейти в состояние a2, при этом выходной символ не формируется; под действием входного символа z2 − в состояние a4 с формированием выходного символа w2; под действием символа z3 − в состояние a3 с формированием выходного символа w3. Далее если на вход автомата, установленного в исходное состояние аm ÍA, в моменты времени t=1,2,…,n подается некоторая последовательность букв входного алфавита (входных символов) ziÍZ, то на выходе автомата будут последовательно формироваться буквы выходного алфавита (выходные символы) wjÍW, при этом автомат будет переключаться в состояния asÍA. Следовательно, с помощью таблиц переходов и выходов можно получить выходную реакцию автомата на любое входное слово.



 В табл. 28 приведена информация о работе D-триггера. Переключение состояний выполняется по формуле t(t+1)= t(t)С V DC.
В табл. 28 приведена информация о работе D-триггера. Переключение состояний выполняется по формуле t(t+1)= t(t)С V DC.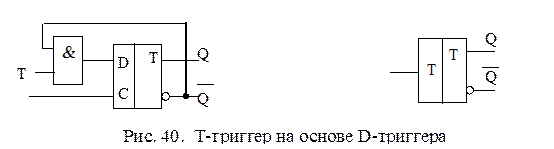


 Табл.30 определяет переходы RS-триггера по формуле t(t+1)=t(t)RVS.
Табл.30 определяет переходы RS-триггера по формуле t(t+1)=t(t)RVS.

 Табл. 31 определяет переходы JK-триггера согласно логической формуле t(t+1)= t(t)J V t(t) K. Таблица 31
Табл. 31 определяет переходы JK-триггера согласно логической формуле t(t+1)= t(t)J V t(t) K. Таблица 31


