
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Деление чисел в прямых кодахСодержание книги
Поиск на нашем сайте
Алгоритм деления с восстановлением остатка состоит в следующем. 1. Выполняется пробное вычитание с формированием первого остатка A1=[Дм]доп+[-Дт]доп. Далее, если А1 < 0, то в первый разряд, расположенный слева от запятой, заносится ноль (0), иначе единица (1) – переполнение и переход к пункту 5. 2. Если Аi < 0, то восстанавливаем предыдущий остаток Ai=Ai+[Дт]доп. 3. Формирование очередного остатка. Ai+1=Ai∙2+[-Дт]доп если Ai+1<0, то в очередной разряд частного справа от запятой записывается ноль (Чт(n)=0), иначе записывается единица (Чт(n)=1). 4. Если достигнута заданная точность частного или получен нулевой остаток Ai+1, то процесс деления окончен и осуществляется переход к пункту 5, иначе переходим к пункту 2 алгоритма. 5. Окончание алгоритма. Из рассмотренного алгоритма видно следующее: 1) необходимо затрачивать время на восстановление остатка; 2) процесс деления нерегулярный, в зависимости от делимого и делителя частное будет содержать нулей больше или меньше, и чем больше нулей, тем больше требуется времени на восстановление остатков. Рассмотрим пример деления чисел.
Как видно из примера, для получения остатка Аi+2 необходимо выполнить Аi+2 = (Ai+1 + ДT) ∙ 21 - ДT = Ai+1 ∙ 21 + 2ДT - ДT = Ai+1 ∙ 21 + ДT Из этого следует, что восстанавливать остаток необязательно. Достаточно сдвинуть полученный отрицательный остаток влево на один разряд и добавить делитель. Это является основой алгоритма для выполнения деления без восстановления остатка. Алгоритм деления без восстановления остатка. 1. Выполняется пробное вычитание с формированием первого остатка A1=[Дм]доп+[-Дт]доп. Далее, если А1 < 0, то в первый разряд, расположенный слева от запятой, заносится ноль (0), иначе единица (1) – что является признаком переполнение и ос4уществляется переход к пункту 5. 2. Формирование очередного остатка. Если Аi < 0, то Ai+1=Ai∙2+[Дт]доп, иначе Ai+1=Ai∙2+[-Дт]доп. 3. Если Аi+1 < 0, то в очередной разряд частного справа от запятой записывается ноль (Чт(n)=0), иначе записывается единица (Чт(n)=1). 4. Если достигнута заданная точность частого или получен нулевой остаток Ai+1, то процесс деления окончен и осуществляется переход к пункту 5, иначе переходим к пункту 2 алгоритма. 5. Окончание алгоритма.
Деление чисел в дополнительных кодах При делении чисел знаковая и значащая части частного формируются раздельно. Знак частного формируется согласно формуле Знак Чт = Знак Дм Å Знак Дт. Основой деления чисел в дополнительных кодах является деление без восстановления остатка. В отличие от деления в прямых кодах, здесь как для определения цифры частного, так и для определения действия сравнивается знак делимого (остатка) со знаком делителя. Ниже приведен алгоритм деления чисел в дополнительных кодах. 1. Выполняется пробное вычитание: если знак Дм ¹ знаку Дт, то первый остаток A1=[Дм]доп+[Дт]доп, иначе A1=[Дм]доп+[-Дт]доп. Далее формируется первый разряд, расположенный слева от запятой - ноль (0), если знак А1 ¹ знаку Дт, иначе единица (1). 2. Формирование очередного остатка. Если знак Аi ¹ знаку Дт, то Ai+1=Ai∙2+[Дт]доп, иначе Ai+1=Ai∙2+[-Дт]доп. 3. Если знак Аi+1 ¹ знаку Дт, то в очередной разряд частного справа от запятой заносится ноль (Чт(n)=0), иначе - единица (Чт(n)=1). 4. Если достигнута заданная точность частого или получен нулевой остаток Ai+1, то процесс деления окончен, иначе переходим к пункту 2 алгоритма. Пример: Дм = - 0,1011 [ Дм ]доп = 1,0101 Дт = 0,1101 [ Дт ]доп = 0,1101 [-Дт ]доп = 1,0011 На деление Дм и Дт поступают в дополнительном коде
Методы ускорения деления Логические методы основываются на анализе остатка, по виду которого можно сформировать несколько цифр частного в пределах одного такта. При этом Дт выбирается (формируется) таким образом, чтобы после запятой шла единица, то есть он нормализован. Если очередной остаток получился настолько мал, что после запятой следует r+1 нулей, то в частное может быть записано r ”0” или ”1”, а остаток может быть сдвинут на r разрядов влево. Итак, для осуществления названных методов ускорения кроме устройства управления делением требуется логическая схема, осуществляющая две функции: 1) сдвиг модулей делителя и делимого до тех пор, пока у модуля делителя после запятой не останется ни одного нуля; 2) выявление остатков вида 0,0…01 или 1,1…10. Степень сложности логической схемы определяется количеством разрядов, участвующих в косвенном сравнении модулей делителя и делимого (остатков). Обычно реализация логических методов ускорения при делении несколько сложнее, чем при умножении. При делении необходимо либо каждый остаток переводить в прямой код, либо, если остаток оставить в дополнительном коде, анализировать два разряда одновременно 0,0… или 1,1….
Двоично-десятичные коды Пусть число A представлено в системе счисления с основанием r:
Цифры ai будем представлять двоичными разрядами d1,d2,…,dm. Каждому двоичному разряду припишем веса p1,p2,…,pm. Тогда каждый разряд ai числа A будет иметь вид
где n и m определяют общее число двоичных разрядов. Если каждый разряд числа имеет вес и при r≠2k не выполняется равенство pk=r ∙ pk-1, то системы принято называть взвешенными. Количество разрядов m должно удовлетворять выражению m ≥ log2r. Если десятичное число записано в виде (4), то будем говорить, что число представлено в двоично-десятичном коде. Наибольшее распространение из них получили коды, в которых десятичная цифра представляется двоичной тетрадой (BCD-коды). Существует множество способов кодирования десятичных цифр. Существенным при этом является простота представления инверсных кодов и простота выделения (формирования) сигнала переноса из цифры в цифру. Сформулируем набор требований, позволяющих упростить выполнение арифметических операций и операций перевода чисел. § Четность, состоит в том, что четным десятичным цифрам соответствуют только четные двоичные коды и наоборот. Это обеспечивает эффективность операций округления, умножения и деления чисел в BCD-кодах. § Дополняемость, заключается в том, что сумма двоичного кода и инверсного ему кода любой десятичной цифры должна быть равна 9. Это обеспечивает эффективность операции алгебраического сложения в BCD-кодах. § Упорядоченность, то есть большей десятичной цифре соответствует большая тетрада и наоборот. § Единственность представления десятичной цифры двоичной тетрадой. § Взвешенность, то есть каждому разряду двоичного представления десятичной цифры поставлен в соответствие вес. Это обеспечивает эффективность всех арифметических и логических операций в BCD-кодах. Если каждая десятичная цифра кодируется соответствующим двоичным эквивалентом, то такое кодирование называется кодом прямого замещения. BCD-код – код, взаимодополняемый до 15. Это создает некоторые неудобства при суммировании чисел - ввод поправки в некоторых случаях. В то же время этот код имеет одно существенное достоинство – аддитивность: сумма кодов равна коду суммы. 0011 код 3 0101 код 5
Основной недостаток этого кода заключается в том, что инверсия какой- либо цифры оказывается цифрой, дополняющей данную цифру до 15, а не до 9. a = 0100
В табл. 4 показаны различные способы кодирования десятичных цифр. Таблица 4
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 522; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.96 (0.01 с.) |

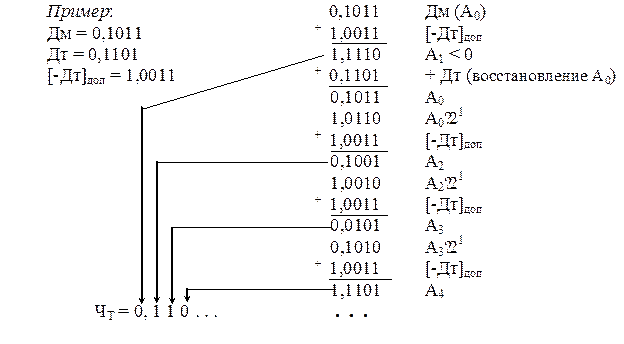



 , а все число
, а все число , (4)
, (4) 1000 код 8
1000 код 8

 a = 1011
a = 1011 


