
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Умножение с хранением переносовСодержание книги
Поиск на нашем сайте
Время, затрачиваемое на сложение двоичных чисел, состоит из времени, необходимого для поразрядного сложения, и времени на формирование переноса tсл = tÅ + tпер. Поразрядное сложение является элементарной операцией, и время на эту операцию может быть сокращено путем использования более быстродействующих элементов. В то же время если исключить необходимость выполнения межразрядных переносов при сложении, то время умножения уменьшится на tпер. Переносы, формируемые при сложении, записываются в отдельный регистр. Содержимое этого регистра добавляется в сумматор вместе с очередым частичным произведением. При этом сложение может выполняться паралельно по всем разрядам. На последнем такте (при умножении на последний разряд множителя) сложение выполняется с учетом межразрядных переносов. В заключение следует отметить, что этот метод используется с алгоритмом A. Пример: Мн = 0,1011 Мт= 0,1101 0,0000 0,0000 регистр переносов
0,1011 0,0000 регистр переносов 0, 0 101 1
0,0101 1 0,0000 регистр переносов 0, 0 010 11
0,1001 11 0,0010 регистр переносов 0, 0 100 111
1,0001 111 0, 1 000 1111
Умножение на два разряда множителя одновременно Разбиение множителя на группы длиной k разрядов означает переход к новой системе счисления с основанием 2k. Если при этом удается сократить количество элементарных действий, выполняемых при умножении (сложение и сдвиги), то сокращается время умножения. Остановимся более подробно на умножении на два разряда множителя за один такт (k=2). Это связано с анализом пар разрядов множителя. Возможны четыре случая сочетания разрядов множителя: 00, 01, 10, 11. Умножение на каждую из пар разрядов множителя должно выполняться за один такт автоматного времени, то есть в каждом такте умножения должно выполняться не более одного сложения. Рассмотрим умножение на эти пары на примере алгоритма А. В случае пары 00 необходимо выполнить только сдвиг частичной суммы на два разряда - Для пары 01 выполняется добавление множимого в сумматор с последующим сдвигом суммы на два разряда - При наличии пары 10 возможны следующие варианты действий: a) б) в) г) При умножении на пару 11 (к частичной сумме необходимо добавить утроенное множимое) ее можно представить в виде 11 = (22 - 1) Мн ∙ 11= Мн∙(22 - 1) = Мн∙22- Мн, то есть в текущем такте к частичной сумме добавляется множимое, взятое со знаком минус. Добавление Мн∙22 реализуется путем увеличения на единицу следующей старшей пары разрядов. В табл.1 представлены правила преобразования множителя для системы (0,1,1). Таблица 1
Пример: Мн = 0101
Умножение будем осуществлять согласно алгоритму А. [- Мн]доп = 1.1011 2 Мн = 0.1010 0.0000 + 1.1011 1.1011 1. 11 10 11 + 0.1010 0.1000 11 0. 00 10 0011 0. 00 00 100011 + 1.1011 1.1011 100011 1. 11 10 11100011 + 0.0101 0.0011 11100011 0. 00 00 1111100011 Время умножения на два разряда множителя одновременно Появление любой из рассматриваемых пар множителей равновероятно. Следовательно, время умножения на два разряда множителя может быть выражено следующим соотношением:
Умножение на четыре разряда одновременно В этом случае с помощью приема, аналогичного приему, использованному в случае умножения на два разряда одновременно, можно рассматривать сразу тетраду двоичных разрядов. Может быть выведено общее правило сокращенного умножения: 1. Если цифра множителя bi-1 < r/2, то 2. Если цифра множителя bi-1 ³ r/2, то
Пример: Мн = 011 Мт = С49
Можно заранее заготовить кратные множители: Мн, 2Мн, 4Мн, поместив их в дополнительные регистры. Это позволит сократить время, необходимое для формирования частичного произведения [+7Мн]доп = 0.10101 [+5Мн]доп= 0.01111 [+4Мн]доп= 0.01100 [-7Мн]доп = 1.01011 [-4Мн]доп = 1.10100 0.00000 + 1.01011 1.01011 1. 1111 0 1011 + 0.01111 0.01101 1011 0. 0000 0 1101 1011 + 1.10100 1.10100 1101 1011 1. 1111 1 0100 1101 1011 + 0.00011 0.00010 0100 1101 1011 0. 0000 00010 0100 1101 1011
|
|||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 465; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.96 (0.006 с.) |


 + 0,1011
+ 0,1011  = Мн b4
= Мн b4
 2-1
2-1 + 0,0000
+ 0,0000  = Мн b3
= Мн b3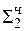
 + 0,1011
+ 0,1011  = Мн b2
= Мн b2
 = Мн b1
= Мн b1
 2-2.
2-2. 2-2.
2-2. 2-2, то есть в этом случае происходят два сложения, что противоречит требованию;
2-2, то есть в этом случае происходят два сложения, что противоречит требованию; 2-2, в этом случае требуется дополнительный регистр для хранения удвоенного Мн;
2-2, в этом случае требуется дополнительный регистр для хранения удвоенного Мн; 2-2, что соответствует добавлению к частичной сумме сдвинутого на один разряд влево множимого;
2-2, что соответствует добавлению к частичной сумме сдвинутого на один разряд влево множимого; 2-1, то есть частичная сумма сдвигается на один разряд вправо до и после добавления к ней множимого.
2-1, то есть частичная сумма сдвигается на один разряд вправо до и после добавления к ней множимого. 11
11
 Мт = 11000111
Мт = 11000111 Мтп = 0101001001
Мтп = 0101001001
 = -Mн
= -Mн
 = 2Mн
= 2Mн
 ∙ 2-2 (
∙ 2-2 ( ∙ 2-4)
∙ 2-4) =-Mн
=-Mн
 = Mн
= Mн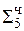
 = (n/2 + 1) [0,75∙(tсл + tсдв) + (0,25∙tсдв], где n – количество разрядов множителя.
= (n/2 + 1) [0,75∙(tсл + tсдв) + (0,25∙tсдв], где n – количество разрядов множителя.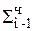 +
+ 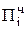 , где
, где  = Мн bi.
= Мн bi. , где
, где  Анализ четырех двоичных разрядов одновременно дает возможность осуществить сдвиг на четыре разряда за один такт.
Анализ четырех двоичных разрядов одновременно дает возможность осуществить сдвиг на четыре разряда за один такт.
 Мтп = 1457
Мтп = 1457 , равного от нуля до семи множимых.
, равного от нуля до семи множимых. =-4Mн
=-4Mн


