
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нахождение множества простых импликантСодержание книги
Поиск на нашем сайте Преобразование исходного покрытия С0 комплекса К в множество простых импликант Z осуществляется с помощью операции умножения кубов.В результате первого шага (С0*С0) (табл. 16) предусматривается выявление как новых кубов Сy (первой и более высокой размерности), так и кубов, которые не образуют новых кубов (включаются в множество Z0). Из полученных новых кубов образуется множество А1. Также формируется множество В1=С0-Z0. Для следующего шага получения множества Z формируется множество С1=А1U В1. Для уменьшения мощности множества кубов С1 выполним операцию поглощения (удаления) кубов, образующих множество С1, кубами из множества А1 (А1ÍС1). Таблица 16
Для рассматриваемого примера получим:
1х10
1х10 х110 1х10 А1 = х110 хх01 после выполнения 000х
хх01 0х10 поглощения хх01 0000 В1 х010 Z0=Ø 0х01 0х10 1х01 Среди кубов С0, возможно, находятся такие кубы, которые с кубами множества А1 могут дать новые кубы или оказаться простыми импликантами после второго шага (С1*С1). При формировании таблицы для выполнения операции С1*С1 (табл. 17) следует учесть, что В1*В1 уже выполнялось на шаге С0*С0. Следовательно, С1*С1=(А1UВ1)*(А1UВ1)=(А1*А1)U(А1*В1)U(В1*А1)U(В1*В1)=(А1*А1)U(А1*В1). Таблица 17
В результате выполнения умножения С1*С1 получим: А2={хх10},
   00х0 . 00х0 .
000х Необходимо отметить, что куб хх01 не дал нового куба. Но это куб второй размерности и новые кубы может дать на третьем шаге (С2*С2). Поэтому его не следует включать в число кубов, образующих множество Z1.
х010 х010 хх01 0х10 0х10 хх01
Таблица 18
Таким образом, получим А3= Ø, следовательно, новых кубов нет.
  хх10 . хх10 .
хх01 В3=С2-Z2= Ø; C3=A3UB3= Ø. На этом процесс выявления простых импликант окончен.
хх01 хх10 Необходимо выяснить, не содержатся ли в этом множестве “лишние” простые импликанты. Определение L-экстремалей Множество Z может быть избыточным. Прежде всего необходимо выявить обязательные простые импликанты, называемые в алгоритме извлечения L-экстремалями. L-экстремаль – это куб, который (и только он) покрывает некоторую вершину из множества L, не покрываемую никаким другим кубом из множества Z. Для определения L-экстремалей воспользуемся операциями вычитания (#) (табл. 19) и пересечения (∩) кубов (табл.20). В табл. 19 z Í Z – некоторая простая импликанта, из которой вычитаются остальные Z-z. Таблица 19
Таким образом, из таблицы получено множество L-экстремалей.
1. Если результат вычисления будет Ø хотя бы в одном, любом случае, то это значит, что среди простых импликант есть такие кубы, которые покрывают уменьшаемый, а следовательно, этот уменьшаемый не может быть L-экстре-малью. 2. Если же полученный результат не Ø, то в противоположность предыдущему утверждению уменьшаемый куб оказывается кубом большей размерности по отношению к другим простым импликантам. 3. Что касается простых импликант, ”удаленных” от уменьшаемой, то они с ней дают координаты ”y” и, таким образом, остается уменьшаемый куб при вычитании этих ” удаленных” кубов. После выявления L-экстремалей следует выяснить, не являются ли некоторые из них простыми импликантами, остатки которых покрывают только некоторое подмножество кубов комплекса N, которое нет необходимости покрывать, вводя в минимальное покрытие соответствующие наборы. Для этого необходимо выполнить операцию пересечения остатков, полученных при выполнении операции z#(Z-z) с кубами из комплекса L. Во множестве E необходимо оставить только те кубы, остатки от которых пересекаются с кубами из комплекса L. Таблица 20
Из таблицы видно, что куб 1x01 не пересекается с кубами комплекса L. Однако куб x101 имеет с кубом 0x01 (из комплекса L) общую вершину 0101. Оба куба (1x01, x101) входят в куб более высокой размерности xx01 (L-экстремаль). Таким образом, куб 1x01, образованный на комплексе N, позволил уменьшить цену схемы. Выясним далее, какие из вершин комплекса L не покрываются L-экстремалями. Для этого из каждого куба комплекса L вычтем (#) элементы множества Е (табл.21). В результате вычитания получим L1=L#Е. Таблица 21
Из таблицы видно, что L1={0000}. Однако не покрытые L-экстремалями кубы должны быть покрыты другими импликантами из множества. Z=Z-E= Теперь из полученного множества Z надо выбрать минимальное число кубов с минимальной ценой (максимальной размерностью), чтобы покрыть непокрытые L-экстремалями элементы комплекса L. Выбор так называемого немаксимального куба осуществляется с помощью операции частичного упорядочивания кубов (табл. 22). Куб a будет немаксимален по отношению к кубу b, если выполняются одновременно два условия: 1) Сa ≥ Cb, где Са – цена куба а; 2) a ∩ L1 Í b ∩ L1, куб b покрывает не меньше кубов чем куб а. Z
Следовательно, кубы а и b равноценны и для покрытия вершины 0000 можно выбрать любой из них в качестве экстремали второго порядка Е¢2={000x} или E¢¢2={00x0}. Следовательно, могут быть получены две тупиковые формы.
Минимизация ФАЛ методом преобразования логических выражений Рассмотрим подход к упрощению ФАЛ, заключающийся в применении к ней скобочных преобразований. Пусть имеется функция f=x1x3x4x6+x2x3x4x6 + x5x6 + x7. Применим к ней скобочные преобразования, в результате чего получим функцию f=((x1+x2)x3x4 + x5)x6 + x7. Из выражений видно, что цена схемы до минимизации была равна 14, после стала равна 11. Таким образом, общая стоимость схемы сократилась, однако исходной функции соответствовала схема, имеющая два уровня элементов, а преобразованной − пять уровней. Таким образом, полученная схема будет работать примерно в 2,5 раза медленнее исходной.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 419; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.96 (0.011 с.) |


 00х0
00х0


 00х0 000х А1 00х0
00х0 000х А1 00х0 000х С1= х010 Þ операции Þ С1= х110
000х С1= х010 Þ операции Þ С1= х110



 1х10 хх10
1х10 хх10
 х110 1х10
х110 1х10 ,
,
 00х0
00х0 .
.
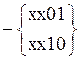
 .
.
 - первая тупиковая форма (рис. 30).
- первая тупиковая форма (рис. 30). - вторая тупиковая форма.
- вторая тупиковая форма.



