
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Умножение в дополнительных кодахСодержание книги
Поиск на нашем сайте Умножение чисел в дополнительных кодах может выполняться по любому из рассмотренных выше четырех алгоритмов, но отличается тем, что для получения верного результата необходимо вводить поправки. Умножение правильных дробей и целых чисел имеет некоторые различия. Рассмотрим вначале умножение дробных чисел. Возможны четыре случая знакосочетания сомножителей. 1) Мн>0, Мт>0. В этом случае дополнительный код сомножителей совпадает с прямым кодом и умножение выполняется по правилам умножения в прямых кодах, в результате чего получается верный результат. 2) Мн>0, Мт<0. Так как Мн и Мт имеют разные знаки, то результат будет иметь отрицательный знак. Следовательно, результат должен быть представлен в дополнительном коде [Мн∙Мт]доп=2-Мн∙Мт. Для формирования произведения выполним умножение Мн на Мт¢ (дополнение): Мн∙Мт¢= Мн ∙(1 - Мт)= Мн - Мн∙Мт.
Δ=2-Мн∙Мт- Мн + Мн∙Мт=2-Мн=[-Мн]доп=[ [Мн]доп]доп и должна быть внесена в полученный результат в качестве поправки. Пример: Мн = 0,1011 (алгоритм умножения А) Мт = - 0,1101 Δ= [- Мн]доп = 1,0101 [- Мт]доп = 1,0011 0,0000
0,1011 0, 0 101 1 + 0,1011
0 ,1 000 01 0, 0 10 0001 0, 0 010 0001 + 1,0101 Δ = [- Мн]доп (поправка)
- 0,1000 1111 Mн ∙ Mт В этом примере, а также в некоторых примерах, следующих ниже, происходит переполнение разрядной сетки, в результате которого искажаются и знаковая и значащая часть числа. Для коррекции (восстановления верного значения) производится немодифицированный сдвиг. В результате этого знаковый разряд сдвигается в значащую часть, а знаковый разряд меняет свое значение на противоположное. 3) Mн<0, Mт>0. Аналогично предыдущему случаю [Мн∙Мт]доп=2-Мн∙Мт, Мн¢∙Мт= (1 - Мн)∙Мт= Мт - Мн∙Мт. Таким образом, погрешность умножения равна разности [Мн Мт]доп и Мт∙Мн¢.
Использовать этот вариант неудобно, так как нужно вводить поправку [-Mт]доп в конце умножения, а в результате сдвигов Мт постепенно исчезает на регистре множителя и для поправки нужно либо вводить дополнительный регистр, либо вносить поправку в сумматор на первом такте умножения. При этом знакосочетании возможно умножение без ввода поправки. Рассмотрим этот вариант на примере умножения по алгоритму Г (это справедливо и для других алгоритмов). Мн∙Мт = А ∙ В = [ A ∙ b1∙ 2-1 ]доп + [ A ∙ b2∙ 2-2 ]доп+... + [A∙ bn∙ 2-n ]доп. На основании теоремы, доказывающей что сумма дополнительных кодов есть дополнительный код суммы, получаем [ A ∙ b1∙ 2-1 + A ∙ b2∙ 2-2 +... + A∙ bn∙ 2-n ]доп = [Мн ∙Мт]доп. В этом случае поправка вводится автоматически на каждом этапе умножения. Пример: Mн = -0,1011 Mт = 0,1101
0,00000000 + 1, 1 0101000
+ 1, 11 010100
1,01110001 [Mн ∙ Mт]доп -0,10001111 Mн ∙ Mт 4) Mн<0, Mт<0. Mн ∙ Mт = 2 - [Mн ∙ Mт]доп [Mн]доп ∙ (1 - Mт) = [Mн]доп - [Mн]доп ∙ Mт = [Mн]доп - [Mн ∙ Mт]доп
Пример: Mн = - 0,1011 умножение будем выполнять Mт = - 0,1101 по алгоритму умножения Г [Mн]доп = 1,0101 [Mт]доп = 1,0011 Δ =[-Mн]доп = 0,1011 0,00000000 + 1, 111 01010
+ 1, 1111 0101
1,11011111
0,10001111 [Mн∙ Mт]доп Далее коротко остановимся на умножении целых чисел. При представлении целых чисел в дополнительном коде знаковый разряд входит в число n разрядов. Следовательно, при умножении целых чисел (в отличие от дробных) в дополнительных кодах знаковый разряд участвует в умножении наряду со значащими. То есть умножение ведется на [Mт]доп , а не на Мт ¢. 1) Mн > 0, Mт > 0. Как отмечалось выше, в этом случае умножение выполняется по правилам умножения чисел в прямых кодах. 2) Мн>0, Mт<0, [Мт]доп = 2n – Мт.
Пример: Mн = +110 Mт = -101 [Mн]доп = 0.110 [Mт]доп = 1.011
0.000 + 0.110 0.110 0. 0 11 0 + 0.110 1.001 0 0. 1 00 10 0. 01 0 010 + 0.110 1.000 010 0. 1 00 0010 + 1.010 1.110 0010 [Mн×Mт]доп - 001 1110 Mн×Mт 3) Мн<0, Мт>0. Здесь, как и при умножении дробных чисел, возможны два случая: a) с вводом поправки в получаемое произведение [Мн]доп = 2n – Mн. Как и ранее, требуется получить [Мн∙Мт]доп= 22n - Мн∙Мт. Получаем (2n - Мн) ∙ Мт = 2n ∙ Мт - Мн∙Мт.
б) вариант без ввода поправки рассмотрим применительно к алгоритму умножения Г (как и ранее это справедливо и для других алгоритмов): Mн∙Mт = A∙B = [A ∙ b1 ∙ 2-1 ]доп + [A ∙ b2 ∙ 2 -2]доп+- ... + [A ∙ bn ∙ 2-n]доп= =[A ∙ b1 ∙ 2-1 + A ∙ b2 ∙ 2 –2 +- ... + A ∙ bn ∙ 2-n]доп=[Мн∙Мт]доп. Пример: Мн = -110 Мт = 101 [Мн]доп = 1.010 [Мт]доп = 0.101 b1 ... b4 0.0000000 + 0. 0 000000 0.0000000 + 1. 11 01000 1.1101000 + 1. 1111 010 1.1100010 4) Mн < 0 Mт < 0 При этом сочетании знаков сомножителей в результате должно быть получено: [Mн]доп = 2n – Mн, [Mт]доп = 2n – Mт, Mн ∙Mт = 22n - [Mн Mт]доп. При умножении [Mн]доп∙[Mн]доп получается: [Mн]доп∙[Mн]д =[Mн]доп (2n - Mт) = 2n [Mн]доп - Пример: Мн = -110 Mт = -101 [Mн]доп = 1.010 [Mт]доп = 1. 011 b1 ... b4
При умножении используем алгоритм Г. 0.0000000 1. 1 010000 1.1010000 1. 111 0100 1.1000100 1. 1111 010 1.0111110 0.110 0.0011110 Mн Mт
|
||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 482; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.96 (0.009 с.) |


 Таким образом, погрешность Δ умножения равна разности [Мн∙Мт]доп. и Мт∙Мн¢
Таким образом, погрешность Δ умножения равна разности [Мн∙Мт]доп. и Мт∙Мн¢
 + 0,1011
+ 0,1011 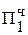 = Мн b4
= Мн b4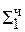
 = Мн b3
= Мн b3 1,0000 1
1,0000 1  (произошло переполнение)
(произошло переполнение) ∙ 2-1 (
∙ 2-1 ( ∙ 2-1) ∙ 2-1
∙ 2-1) ∙ 2-1 ∙ 2-1 ((
∙ 2-1 (( 1,0111 0001
1,0111 0001  =[Mн ∙ Mт]доп
=[Mн ∙ Mт]доп
 Δ=2-Мн∙Мт- Мт + Мн∙Мт=2-Мт=[-Мт]доп=[ [Мт]доп]доп.
Δ=2-Мн∙Мт- Мт + Мн∙Мт=2-Мт=[-Мт]доп=[ [Мт]доп]доп. = [Mн ∙ b1 ∙ 2-1]доп
= [Mн ∙ b1 ∙ 2-1]доп 1,10101000
1,10101000  = [Mн ∙ b2 ∙ 2-2]доп
= [Mн ∙ b2 ∙ 2-2]доп 1,01111100
1,01111100  + 1, 1111 0101
+ 1, 1111 0101  = [Mн ∙ b4 ∙ 2-4]доп
= [Mн ∙ b4 ∙ 2-4]доп
 Δ=2 - [Mн ∙ Mт]gдоп - [Mн]доп + [Mн ∙ Mт]доп = 2 - [Mн]доп = [[Mн]доп]доп
Δ=2 - [Mн ∙ Mт]gдоп - [Mн]доп + [Mн ∙ Mт]доп = 2 - [Mн]доп = [[Mн]доп]доп
 = [Mн ∙ b3 ∙ 2-3]доп
= [Mн ∙ b3 ∙ 2-3]доп 1,11101010
1,11101010 
 = [Mн ∙ b4 ∙ 2-4]доп
= [Mн ∙ b4 ∙ 2-4]доп

 + 0, 1011 0000 Δ (поправка)
+ 0, 1011 0000 Δ (поправка)
 = [- Mн]доп = 1.010
= [- Mн]доп = 1.010
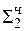 (возникло переполнение)
(возникло переполнение) ∙2-1
∙2-1
 = 22n - Мн∙Мт - 2n ∙ Мт + Мн∙Мт = 2n(2n - Мт) = [-Мт]доп ∙ 2n;
= 22n - Мн∙Мт - 2n ∙ Мт + Мн∙Мт = 2n(2n - Мт) = [-Мт]доп ∙ 2n;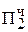 = [MH ∙ b2]доп ∙ 2-2
= [MH ∙ b2]доп ∙ 2-2
 = [MH ∙ b4]доп ∙ 2-4
= [MH ∙ b4]доп ∙ 2-4
 = [Mн∙b1]доп∙2-1
= [Mн∙b1]доп∙2-1




