
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 1. Системы счисления и кодыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Тема 1. Системы счисления и коды
Системой счисления называют совокупность приёмов и правил для записи чисел. Системы счисления делятся на позиционные и непозиционные. В непозиционных системах любая цифра соответствует некоторому фиксированному числу. Пример непозиционной системы – римская система счисления. Более часто используются позиционные системы, в которых целое n -разрядное положительное число записывается в виде последовательности символов (цифр) из разрешенного для этой системы набора:(en- 1 ...ер ...е 1 е 0) q. В такой записи вес каждого символа ер в результирующем значении числа равен qp, где q – основание системы счисления, p – номер позиции символа в записи числа (p = 0 …n – 1):
или
Основание позиционной системы счисления определяет её название. Позиция символа en –1 в общей записи числа носит название старшего значащего разряда (СЗР), а е 0 – младшего значащего разряда (МЗР). Для представления нецелых положительных чисел используется последовательное описание целой и дробной части чисел с использованием разделителя – запятой или точки в зависимости от принятого соглашения:
Отрицательные числа описываются путем добавления перед старшим значащим разрядом дополнительного символа (например, минуса). Наиболее привычной является д есятичная система счисления, используемая нами в повседневной жизни. Основанием системы является число 10. Для записи чисел используются символы 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Для изображения чисел больших 9 применяется позиционный способ записи числа:
–
При реализации цифровых устройств десятичная система не применяется, так как, в частности сложно спроектировать электронное оборудование таким образом, чтобы оно работало с 10 различными уровнями напряжения (каждый представлял бы один десятичный символ от 0 до 9). По этой причине почти каждая цифровая система использует двоичную систему счисления в качестве базовой для всех операций, хотя часто в сочетании с двоичной применяются и другие системы счисления. Двоичная система. Основанием системы является число 2. Для записи чисел используются символы 0, 1. Для изображения чисел больших 1 применяется позиционный способ записи числа:
В двоичной записи числа один двоичный разряд часто обозначается термином бит. В последнем примере три бита слева от разделителя (запятой) представляют целая часть числа, а два бита справа от разделителя – его дробную часть. Самый левый бит – старший значащий бит, у него наибольший вес (23), а младшим значащим битом выступает самый правый бит в записи числа с наименьшим весом (2-2). Восьмеричная система. Основанием восьмеричной системы счисления является число 8. Для записи чисел используются цифры 0, 1, 2, 3, 4, 5, 6, 7. Для изображения чисел больших 7 применяется позиционный способ записи числа:
Шестнадцатеричная система. Основанием системы является число 16. Для записи чисел используются символы 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F (шестнадцатеричной системе счисления необходимо 16 цифр, поэтому для нее десятичные цифры 0…9 дополняются буквами A…F., имеющими десятичные эквиваленты 10…15). Для изображения чисел больших 15 применяется позиционный способ записи числа:
Системы счисления с основанием 16 и 8 применяются для краткой записи многоразрядных двоичных чисел в цифровых системах. Тема 8. Цифровая реализация основных Функциональных устройств телекоммуникаций
Возможность цифровой реализации сложных устройств телекоммуникаций рассмотрим на примере проектирования функциональной схемы цифрового частотного модулятора Пусть в соответствии с техническими требованиями цифровой частотный модулятор (ЦЧМ) должен вырабатывать синусоидальное колебание с линейно изменяющейся частотой от 500 кГц до 8,5 МГц с периодом повторения 18,4 мс. Один из возможных способов реализации ЦЧМ представлен на рисунке 8.1.
Рисунок 8.1 – Обобщенная структурная схема цифрового частотного модулятора Процесс генерации заключается в вычислении на каждом такте текущего значения фазы частотно-модулированного колебания в двоичном виде и затем выборки по коду фазы соответствующего значения мгновенного значения синусоидального сигнала из постоянного запоминающего устройства (ROM Sin). Таким образом, реализация ЦЧМ сводится к реализации алгоритма вычисления фазы. Выражение для частоты линейно изменяющегося синусоидального колебания может быть записано в виде:
ω(t) = ω0 + ∆ω t/τ (8.1)
Учитывая интегральную зависимость межу мгновенной частотой и фазой синусоидального колебания, мгновенная фаза определяется в виде:
φ(t) = ∫ω(τ) dτ = ω0t + ∆ω t2/2τ, (8.2)
где ω0 = 2π·500 кГц; ∆ω = 2π·(8500 – 500) ·10 3 Гц = 2π ·8 ·10 6 Гц; τ – время присутствия сигнала, равное 18,4 мс.
Так как предполагается цифровая реализация вычислителя фазы, то для дискретных моментов времени, соответствующих тактовым точкам мгновенная фаза определяется как
φ(i·∆t) = ω0·i·∆t + ∆ω·(i·∆t)2/2τ, (8.3)
Учитывая, что ∆t = 1/fт, запишем выражение (8.3) в следующем виде:
φi = (ω0/fт)·i + (∆ω/2τ fт2)·i2 (8.4)
Обозначим δφ = (∆ω/2τ fт2) и перепишем выражение (8.4):
φi = δφ(ω0/fт)·i + i2 = δφ(N0·i + i2) = δφ·i·(N0 + i), (8.5)
N0 = (ω0·2τ fт)/∆ω (8.6) N0 = 73360
Таким образом формула (8.5) – это алгоритм вычисления фазы линейно изменяющегося синусоидального колебания. Структурная схема вычислителя фазы по этому алгоритму представлена на рисунке 8.2.
Рисунок 8.2 – Структурная схема вычислителя фазы, реализующего алгоритм (8.5)
Рассчитаем количество точек на период, необходимых для описания сигнала синусоиды:
N = 2π/δφ (8.7) N = 4695040 точек
Рассмотрим возможности реализации схемы по рисунку 8.2. Для обеспечения требуемой точности сумматор должен иметь разрядность, эквивалентную числу точек на период, т.е. 23. Схема умножения, должна иметь разрядность, эквивалентную числу N0, т.е. 17. Видим, что реализация данной схемы представляется сложной и еще потому, что схема возведения в квадрат оперирует переменным числом. Наряду с прямым вычислением фазы колебания с линейным изменением частоты можно использовать рекуррентный алгоритм, представляемый в обобщенном виде:
φi+1 = φi + ∆φi, (8.8)
и в соответствии с которым последующее значение фазы вычисляется путем суммирования текущего значения фазы с рассчитанным приращением фазы. Приращение фазы на i -том такте составляет:
∆φi =φi+1 - φi = δφ(N0·(i + 1) + (i + 1)2 – N0·i – i2) = δφ(N0 + 2i + 1) (8.9)
Таким образом, формулы (8.8) и (8.9) являются алгоритмом вычисления фазы, для реализации которого можно предложить следующий вариант построения схемы вычисления фазы (рисунок 8.3).
Рисунок 8.3 – Обобщенная структурная схема цифрового частотного модулятора, реализующего алгоритм (8.8), (8.9)
Анализ этой схемы показывает, что сложность ее реализации заключается только в построении сумматоров, разрядность которых равна 23. Так как для представления телевизионного сигнала с необходимой точностью достаточно 256 уровней квантования, что соответствует 8-ми битному кодированию отсчетов, определяем минимальное приращение напряжения, приходящееся на шаг квантования: ∆U = 2/256 = 1/128, где 2 – это размах синусоиды в относительных единицах. Задавшись условием, что ошибка в определении фазы не должна превышать ошибку квантования, определяем минимальное приращение фазы, соответствующее приращению уровня на шаг квантования. С учетом того, что максимальная крутизна синусоидального колебания соответствует участку перехода функции через ноль, минимальное приращение фазы составит:
δφ* = arcsin (∆U) ≈ ∆U (8.10)
δφ* = 1/128
Определим количество точек фазы, приходящихся на период 2p, исходя из минимального приращения фазы на отсчет δφ*:
N* = 2π/ δφ* (8.11)
N* = 804 точки
Выбираем количество точек кратным степени 2 и равным 1024. Пересчитываем минимальное приращение фазы на один отсчет исходя из выбранного количества точек из формулы (8.): δφ* = π/512. Как было сказано выше, сложность построения схемы на рисунке 8.3 заключается в реализации 23-х разрядного сумматора. Можно упростить построение схемы, если отбросить несколько младших значений суммируемого числа. Отбрасываем Ку младших значений числа i и получаем эквивалентное ему число Ку·int(i / Ку) с некоторой ошибкой (int (х) – операция извлечения целой части числа х). Определим эту ошибку, накапливаемую за расчетный цикл, состоящий из Ку тактов:
δц = ∑ j - ∑ Ку·int(i / Ку) = Ку(Ку – 1) / 2, (8.12)
где j изменяется от i до i + Ку – 1. Положительное значение ошибки говорит о том, что истинное значение всегда больше, чем рассчитанное с усечением. Среднее значение ошибки усечения на такт составляет:
δср = δц /Ку = (Ку – 1) / 2 (8.13)
Таким образом, число i можно представить в виде суммы усеченного числа и усредненной ошибки:
i ≡ δср + Ку·int(i / Ку) (8.14)
Теперь с учетом формулы (8.14) найдем ошибку, накапливаемую за счет усечения:
δ*(К) = ∑ (J - δср) = К(К+1)/2 – (К + 1) δср = (К-2δср)(К+1)/2 (8.15)
Путем взятия производной от функции (8.15) по переменной Ку найдем максимальный Ку:
Кмах = (Ку-2)/2 (8.16)
Подставляя (8.16) в (8.15) получим максимальное значение ошибки в цикле из Ку тактов:
δ*(Кмах) = -Ку2 / 8 (8.17)
Знак минус в выражении (8.17) говорит о том, что усеченное значение всегда (за исключением номеров тактов кратных Ку) больше чем истинное. Найдем значение приращения фазы на i-том такте с учетом усечения:
∆φi* = δφ(N0+1+2δср +2Ку·int(i / Ку) (8.18)
∆φi+1* = δφ ·Ку·∑[(N0+1+2δср)/Ку+2int(i / Ку)] (8.19)
∆φi* = δφ · Ку [(N0+1+2δср)/ Ку +2int(i / Ку)] (8.20)
Величина ошибки фазы не должна превышать δφ* = π/512:
δφ Ку2 / 8 ≤ δφ* (8.21)
Отсюда получаем Ку ≤ 191.Выбор конкретного значения Ку диктуется следующими соображениями: Для обеспечения суммирования по модулю 2 необходимо выполнение условия:
δφ* = δφ Ку·2m (8.22)
Так как δφ = π·∆f/τ·fт2, то можем варьировать τ и ∆f для обеспечения выполнения равенства. Изменяя в небольших пределах τ, получаем,что Кумах = = 143, m = 5, т.е. δφ = π/2342912, а τ = 18340 мкс, т.е. значение мгновенной частоты в 8,5 МГц будет достигнуто не в конце активной части поля, а на 36 мкс (приблизительно половина длительности строки) раньше. Тогда N0 = (ω/fт)δφ = = 73216. Получаем, что [(N0+1+2δср)/Ку = 513. Окончательно выражение для приращения фазы на i-том такте выглядит в виде:
∆φi = 513 +int(i / 143) (8.23)
На основании этого синтезируем функциональную схему цифрового частотного модулятора, обеспечивающего формирование в цифровом виде ЛЧМ сигнала (рисунок 8.4).
Рисунок 8.4 – Функциональная схема цифрового частотного модулятора
Серии логических элементов Исторически развитие импульсной и цифровой техники прошло несколько этапов, разработка основных типов логики: 1.РТЛ – резисторно-транзисторная логика. 2.ДТЛ – диодно-транзисторная логика. 3.ТТЛ – транзисторно-транзисторная логика. 4.ТТЛШ - транзисторно-транзисторная логика с диодами Шотки. 5.ЭЛС – эмиттерно-связанная логика. 6.МОП (МДП) – логика на униполярных транзисторах с каналами проводимости p- и n -типов. 7. КМОП (КМДП) – логика на основе униполярных транзисторов с использованием дополняющих комплементарных транзисторов. 8.И2Л – инжекционная интегральная логика. Цифровые интегральные микросхемы выпускаются сериями. Внутри каждой серии имеются объединённые по функциональному признаку группы устройств, имеющие единое конструкторско-технологическое исполнение. Основой каждой серии ИМС является базовый логический элемент. Транзисторно-транзисторная логика (ТТЛ) получила широкое применение в импульсных и цифровых устройствах. Базовый логический элемент ТТЛ состоит из двух частей И и НЕ (рисунок 9.1).
 
  
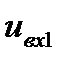 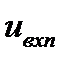 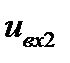
Реализуемое данной схемой логическое уравнение имеет вид: Эквивалентная схема каскада выглядит следующим образом:
      
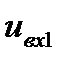 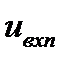 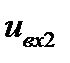
Широкое распространение получила другая схема, на основании которой была выпущена 155 серия. Эта схема приведена на рис. 9.2.
   
  

Данная схема реализует следующее логическое уравнение: Рассмотрим работу схемы более подробно. Если на все входы подаётся Подадим на один из входов 0,т.е. закоротим его на землю. Транзисторы VT1 и VT2 в этом случае будут закрыты, транзистор VT3 будет открыт, но не насыщен, а оставшаяся часть схемы является практически эмиттерным повторителем. Предельное значение входного тока будет ограничиваться резистором Основной недостаток схемы: большое энергопотребление. Достоинства схемы: один источник питания, большой коэффициент разветвления по входу, достаточно высокое быстродействие (переход из одного состояния в другое происходит за 15-20 нс).
Основными характеристиками логических элементов являются: быстродействие, нагрузочная способность (коэффициент разветвления по входу), коэффициент объединения по входу, помехоустойчивость, потребляемая мощность, напряжение питания, уровни логических сигналов. Быстродействие Здесь
Коэффициент объединения по входу определяет максимальное число входов логического элемента. Увеличение числа входов расширяет функциональные возможности, однако при этом ухудшается быстродействие и помехоустойчивость. Потребляемая мощность определяется следующим образом: здесь Напряжение источника питания в разных схемах разное (1В; 3В; 5В). Уровни логических сигналов для ТТЛ имеют следующие величины:
Варианты схем ТТЛ с дополнительными Тема 15. Микропроцессоры
Основные понятия Микропроцессор (МП) − функционально законченное программно-управляемое устройство, предназначенное для обработки данных и управления процессом этой обработки, выполненное в виде одной или нескольких БИС. Микропроцессорная система (МС) − цифровое устройство или цифровая система (система обработки данных, контроля и управления), построенная на базе одного или нескольких МП. Программно-аппаратный принцип построения МС − один из основных принципов их организации. Этот принцип заключается в том, что реализация целевого назначения МС достигается не только аппаратными средствами, но и с помощью программного обеспечения. Микропроцессорная БИС − интегральная микросхема, выполняющая функцию МП или его части. По существу − это БИС с процессорной организацией, разработанная для построения микросистем. МП БИС относятся к особому классу микросхем, одной из особенностей которого является возможность программного управления БИС с помощью определенного набора команд. Кроме МП БИС существуют также интегральные схемы, выполняющие функции памяти и интерфейсов периферийных устройств. Микропроцессорный комплект (микропроцессорные средства) - совокупность конструктивно и электрически совместимых ИС, предназначенных для совместного применения при построении микропроцессорных систем. Включает базовый комплект (процессор или процессорные секции) и расширенный комплект (тактовые генераторы, ЗУ, интерфейсные схемы, контроллеры внешних устройств) Микро-ЭВМ – устройство обработки данных на основе микропроцессорных средств, содержащее процессор, устройства постоянной и оперативной памяти, устройства управления вводом-выводом информации и контроллеры внешних устройств. Микроконтроллер − однокристальная микроЭВМ с небольшими вычислительными ресурсами и упрощенной системой команд, ориентированная на выполнение процедур управления различным оборудованием (а не на производство вычислений). Особенностью микроконтроллеров является расширенная реализация периферийных средств на кристалле. Интерфейс – совокупность унифицированных аппаратных (технических) и программных средств, необходимых для подключения устройств к системе или одной системы к другой. Шина – группа линий передачи информации, объединенных общим функциональным признаком. Магистраль – совокупность шин, связывающих между собой все устройства микропроцессорной системы. Прерывание – временное прекращение выполнения текущей программы и переход к выполнению программы обслуживания устройства, вызвавшего прерывание. Алгоритм – набор предписаний, однозначно определяющих содержание и последовательность выполнения операций для решения определенной задачи. Программа – последовательность инструкций, реализующих алгоритм. Команда – предписание, определяющее шаг процесса выполнения программы. Тема 1. Системы счисления и коды
Системой счисления называют совокупность приёмов и правил для записи чисел. Системы счисления делятся на позиционные и непозиционные. В непозиционных системах любая цифра соответствует некоторому фиксированному числу. Пример непозиционной системы – римская система счисления. Более часто используются позиционные системы, в которых целое n -разрядное положительное число записывается в виде последовательности символов (цифр) из разрешенного для этой системы набора:(en- 1 ...ер ...е 1 е 0) q. В такой записи вес каждого символа ер в результирующем значении числа равен qp, где q – основание системы счисления, p – номер позиции символа в записи числа (p = 0 …n – 1):
или
Основание позиционной системы счисления определяет её название. Позиция символа en –1 в общей записи числа носит название старшего значащего разряда (СЗР), а е 0 – младшего значащего разряда (МЗР). Для представления нецелых положительных чисел используется последовательное описание целой и дробной части чисел с использованием разделителя – запятой или точки в зависимости от принятого соглашения:
Отрицательные числа описываются путем добавления перед старшим значащим разрядом дополнительного символа (например, минуса). Наиболее привычной является д есятичная система счисления, используемая нами в повседневной жизни. Основанием системы является число 10. Для записи чисел используются символы 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Для изображения чисел больших 9 применяется позиционный способ записи числа:
–
При реализации цифровых устройств десятичная система не применяется, так как, в частности сложно спроектировать электронное оборудование таким образом, чтобы оно работало с 10 различными уровнями напряжения (каждый представлял бы один десятичный символ от 0 до 9). По этой причине почти каждая цифровая система использует двоичную систему счисления в качестве базовой для всех операций, хотя часто в сочетании с двоичной применяются и другие системы счисления. Двоичная система. Основанием системы является число 2. Для записи чисел используются символы 0, 1. Для изображения чисел больших 1 применяется позиционный способ записи числа:
В двоичной записи числа один двоичный разряд часто обозначается термином бит. В последнем примере три бита слева от разделителя (запятой) представляют целая часть числа, а два бита справа от разделителя – его дробную часть. Самый левый бит – старший значащий бит, у него наибольший вес (23), а младшим значащим битом выступает самый правый бит в записи числа с наименьшим весом (2-2). Восьмеричная система. Основанием восьмеричной системы счисления является число 8. Для записи чисел используются цифры 0, 1, 2, 3, 4, 5, 6, 7. Для изображения чисел больших 7 применяется позиционный способ записи числа:
Шестнадцатеричная система. Основанием системы является число 16. Для записи чисел используются символы 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F (шестнадцатеричной системе счисления необходимо 16 цифр, поэтому для нее десятичные цифры 0…9 дополняются буквами A…F., имеющими десятичные эквиваленты 10…15). Для изображения чисел больших 15 применяется позиционный способ записи числа:
Системы счисления с основанием 16 и 8 применяются для краткой записи многоразрядных двоичных чисел в цифровых системах.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 1045; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.104.36 (0.01 с.) |

 , (1.1)
, (1.1)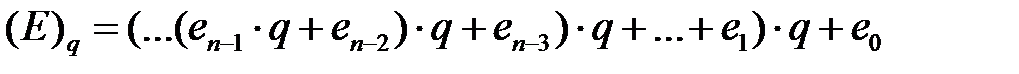 . (1.2)
. (1.2) , (1.3)
, (1.3)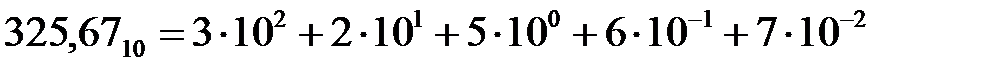 ,
, .
. ,
,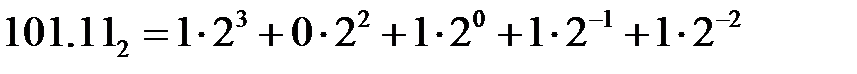 .
.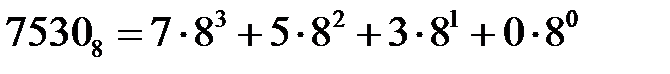 ,
,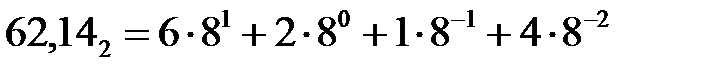 .
.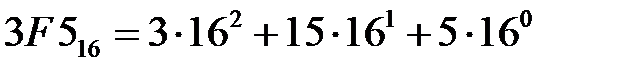 ,
, .
. VTn
VTn



 , то все эмиттерные переходы транзистора VTn закрыты, ток протекает по контуру
, то все эмиттерные переходы транзистора VTn закрыты, ток протекает по контуру 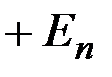 , резистор
, резистор 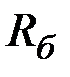 , коллекторный переход транзистора VTn, эмиттерный переход транзистора VT1, резистор
, коллекторный переход транзистора VTn, эмиттерный переход транзистора VT1, резистор 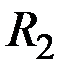 , эмиттерный переход транзистора VT2, земля. В результате потенциал на выходе равен 0,2, т.е. на выходе - 0.
, эмиттерный переход транзистора VT2, земля. В результате потенциал на выходе равен 0,2, т.е. на выходе - 0.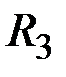 , который защищает схему от коротких замыканий по входу. Диод VD в состоянии 0 по выходу поддерживает транзистор VT3 закрытым.
, который защищает схему от коротких замыканий по входу. Диод VD в состоянии 0 по выходу поддерживает транзистор VT3 закрытым. характеризует среднее время задержки распространения сигнала через логический элемент.
характеризует среднее время задержки распространения сигнала через логический элемент.
 и
и 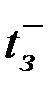 - время задержки перехода из 0 в 1 и из 1 в 0 соответственно. Данные параметры отражены на рис. 9.3.
- время задержки перехода из 0 в 1 и из 1 в 0 соответственно. Данные параметры отражены на рис. 9.3.







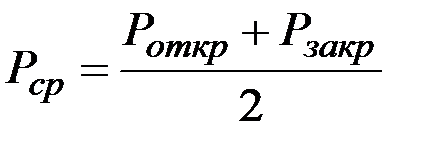
 и
и  - мощности, потребляемые логическим элементом в открытом и закрытом состояниях соответственно.
- мощности, потребляемые логическим элементом в открытом и закрытом состояниях соответственно.



