Цель: научиться переводить числа из одной системы счисления в другую.

 

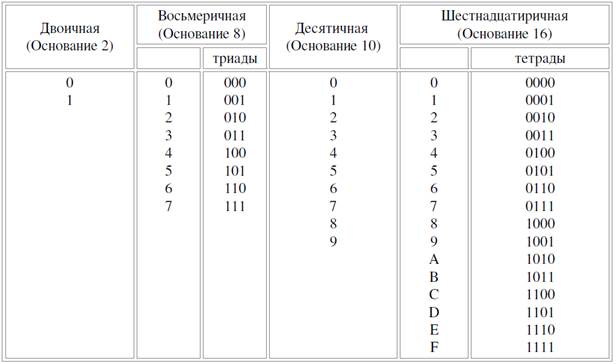
Методические указания.

Под системой счисления понимается способ представления любого числа с помощью некоторого алфавита символов, называемых цифрами.

Все системы счисления делятся на позиционные и непозиционные.

Непозиционными системами являются такие системы счисления, в которых каждый символ сохраняет свое значение независимо от места его положения в числе. Примером непозиционной системы счисления является римская система. К недостаткам таких систем относятся наличие большого количества знаков и сложность выполнения арифметических операций.

Система счисления называется позиционной, если одна и та же цифра имеет различное значение, определяющееся позицией цифры в последовательности цифр, изображающей число. Это значение меняется в однозначной зависимости от позиции, занимаемой цифрой, по некоторому закону. Примером позиционной системы счисления является десятичная система, используемая в повседневной жизни.

Количество p различных цифр, употребляемых в позиционной системе определяет название системы счисления и называется основанием системы счисления "p".

В десятичной системе используются десять цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9; эта система имеет основанием число десять.

Задание 1. Запишите развернутую и краткую формы записи любого числа.

В ЭВМ применяют позиционные системы счисления с недесятичным основанием: двоичную, восьмеричную, шестнадцатеричную. В аппаратной основе ЭВМ лежат двухпозиционные элементы, которые могут находиться только в двух состояниях; одно из них обозначается 0, а другое 1. Поэтому основной системой счисления применяемой в ЭВМ является двоичная система.

Двоичная система счисления. Используется две цифры: 0 и 1.

Восьмеричная система счисления. Используется восемь цифр: 0, 1, 2, 3, 4, 5, 6, 7.

Употребляется в ЭВМ как вспомогательная для записи информации в сокращенном виде. Для представления одной цифры восьмеричной системы используется три двоичных разряда (триада) (Таблица 1).

Шестнадцатеричная система счисления. Для изображения чисел употребляются 16 цифр. Первые десять цифр этой системы обозначаются цифрами от 0 до 9, а старшие шесть цифр латинскими

буквами: 10=A,

11=B,

12=C,

13=D,

14=E,

15=F.

Шестнадцатеричная система используется для записи информации в сокращенном виде. Для представления одной цифры шестнадцатеричной системы счисления используется четыре двоичных разряда (тетрада) (Таблица 1).

 

Таблица 1. Наиболее важные системы счисления.

Перевод чисел из одной системы счисления в другую.

Перевод чисел в десятичную систему осуществляется путем составления

степенного ряда с основанием той системы, из которой число переводится. Затем

подсчитывается значение суммы.

Задание 2.

Перевести 10101101.101 из «2» в «16», «8» и «10» с.с.

При одновременном использовании нескольких различных систем счисления основание системы, к которой относится число, указывается в виде нижнего индекса.

Задание 3. Переведите самостоятельно.

а) Перевести 703.048 из «10» в «2», затем в «8» и наконец, в «16»

б) Перевести B2E.416 из «16» в «10», затем в «8».

Перевод целых десятичных чисел в недесятичную систему счисления осуществляется последовательным делением десятичного числа на основание той системы, в которую оно переводится, до тех пор, пока не получится частное меньшее этого основания. Число в новой системе записывается в виде остатков деления, начиная с последнего.

Задание 4.

а) Перевести 18110 из «10» в «2».

б) Перевести 62210 из «8» в «2», затем в «10».

Перевод правильных дробей из десятичной системы счисления в недесятичную.

Для перевода правильной десятичной дроби в другую систему эту дробь надо последовательно умножать на основание той системы, в которую она переводится. При этом умножаются только дробные части. Дробь в новой системе записывается в виде целых частей произведений, начиная с первого.

Задание 5. Перевести 0.312510

Замечание. Конечной десятичной дроби в другой системе счисления может соответствовать бесконечная (иногда периодическая) дробь. В этом случае количество знаков в представлении дроби в новой системе берется в зависимости от требуемой точности.

Задание 6. Перевести 0.6510 из «10» в «2» с.с. Точность 6 знаков.

Для перевода неправильной десятичной дроби в систему счисления с недесятичным основанием необходимо отдельно перевести целую часть и отдельно дробную.

Задание 7.

Перевести 23.12510 из «10» в «2» с.с.

Необходимо отметить, что целые числа остаются целыми, а правильные дроби дробями в любой системе счисления. Для перевода восьмеричного или шестнадцатеричного числа в двоичную форму достаточно заменить каждую цифру этого числа соответствующим трехразрядным двоичным числом (триадой) (Таб. 1) или четырехразрядным двоичным числом (тетрадой) (Таб. 1), при этом отбрасывают ненужные нули в старших и младших разрядах.

Задание 8.

а)Перевести 305.47 из «8» в «10» с.с.

б)Перевести 7B2.E16 из «16» в «10».

Для перехода от двоичной к восьмеричной (шестнадцатеричной) системе поступают следующим образом: двигаясь от точки влево и вправо, разбивают двоичное число на группы по три (четыре) разряда, дополняя при необходимости нулями крайние левую и правую группы. Затем триаду (тетраду) заменяют соответствующей восьмеричной (шестнадцатеричной) цифрой.

Задание 9.

а) Перевести 1101111001.1101 из «2» в «8» с.с.

б) Перевести 11111111011.100111 из «2» в «16» с.с.

Перевод из восьмеричной в шестнадцатеричную систему и обратно осуществляется через двоичную систему с помощью триад и тетрад.

Задание 10.

Перевести 175.248 "16" с.с.

Двоичная арифметика.

При сложении двоичных чисел в каждом разряде производится сложение цифр слагаемых и переноса из соседнего младшего разряда, если он имеется. При этом необходимо учитывать, что 1+1 дают нуль в данном разряде и единицу переноса в следующий.

Задание 11. Выполнить сложение двоичных чисел:

а) X=1101, Y=101;

б) X=1101, Y=101, Z=111;

При вычитании двоичных чисел в данном разряде при необходимости занимается 1 из старшего разряда. Эта занимаемая 1 равна двум 1 данного разряда.

Задание 12. Заданы двоичные числа X=10010 и Y=101. Вычислить X-Y.

Умножение двоичных чисел производится по тем же правилам, что и для десятичных с помощью таблиц двоичного умножения и сложения.

Пример. 1001* 101=?

Деление двоичных чисел производится по тем же правилам, что и для десятичных. При этом используются таблицы двоичного умножения и вычитания.

Пример. 1100.011: 10.01=

Самостоятельная работа.

Выполнить перевод числа в соответствии с вариантом.

1. Перевести десятичное число А=121 в двоичную систему счисления.

2. Перевести двоичное число А=10001010111,01 в десятичную систему

счисления.

3. Перевести десятичное число А=135,656 в двоичную систему счисления с

точностью до пяти знаков запятой.

4. Перевести двоичное число А=10111011 в десятичную систему счисления

методом деления на основание.

5. Перевести восьмеричное число А=345,766 в двоичную систему счисления.

6. Записать десятичное число А=79,346 в двоичнодесятичной

форме.

7. Перевести десятичную дробь 64

A = 63 9 в двоичную систему счисления.

8. Перевести десятичное число А=326 в троичную систему счисления.

9. Перевести десятичную дробь 40

A = 63 5 в двоичную систему счисления.

10. Перевести десятичное число А=15,647 в двоичную систему счисления.

11. Перевести десятичное число А=1211 в пятеричную систему счисления.

12. Перевести десятичную дробь А=0,625 в двоичную систему счисления.

13. Перевести двоичную дробь А=0,1101 в десятичную систему счисления.

14. Перевести десятичное число А=113 в двоичную систему счисления.

15. Перевести двоичное число А=11001,01 в десятичную систему счисления.

16. Перевести десятичное число А=96 в троичную систему счисления.