
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Пз№1. Выполнение арифметических операций над числами в эвмСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте ОГЛАВЛЕНИЕ ПЗ№1. ВЫПОЛНЕНИЕ АРИФМЕТИЧЕСКИХ ОПЕРАЦИЙ НАД ЧИСЛАМИ В ЭВМ... 2 ПЗ №2. МИНИМИЗАЦИЯ ЛОГИЧЕСКИЗ ФУНКЦИЙ 16 ПЗ №3. РЕШЕНИЕ ЗАДАЧ ПО СИНТЕЗУ ЛОГИЧЕСКИХ СХЕМ 29 ПЗ №4. ОЦЕНКА СПОСОБОВ ВНУТРИМАШИННОГО ПРЕДСТАВЛЕНИЯ ИНФОРМАЦИИ 42 ПЗ №5. РЕШЕНИЕ ЗАДАЧ ПО ОЦЕНКЕ ОСНОВНЫХ ПАРАМЕТРОВ ОЗУ 55 ПЗ №6. СОСТАВЛЕНИЕ АЛГОРИТМОВ И МИКРОПРОГРАММ РАБОТЫ АЛУ 66 ПЗ №7. СОСТАВЛЕНИЕ АЛГОРИТМОВ И МИКРОПРОГРАММ РАБОТЫ УУ 77 ПЗ №8. РАЗРАБОТКА МОДУЛЕЙ ПАМЯТИ НА БИС 84 ПЗ №9. МИКРОПРОГАММИРОВАНИЕ МПУ НА БАЗЕ СМП 98 ПЗ №10 РЕШЕНИЕ ЗАДАЧ РАЗРАБОТКИ АППАРАТНЫХ СРЕДСТВ СВК. 111 ПЗ №11. ПЛАНИРОВАНИЕ ВЫЧИСЛИТЕЛЬНОГО ПРОЦЕССА ПРИ МУЛЬТИПРОГРАММИРОВАНИИ 127 ПЗ №12. РЕШЕНИЕ ЗАДАЧ ПО ОПРЕДЕЛЕНИЮ ПАРАМЕТРОВ ВК 147 ПЗ№1. ВЫПОЛНЕНИЕ АРИФМЕТИЧЕСКИХ ОПЕРАЦИЙ НАД ЧИСЛАМИ В ЭВМ Цель занятия: 1. Освоить практически возможности алгоритмов перевода чисел с использованием различных систем счисления. 2. Научиться применять способы выполнения арифметических операций с применением машинных кодов чисел. 3. Приобрести навыки практической работы с информацией во внутримашинном представлении.
Теоретические сведения Системой счисления называется способ изображения чисел с помощью ограниченного набора символов, имеющих определенные количественные значения. Систему счисления образует совокупность правил и приемов представления чисел с помощью набора символов (цифр и букв). Системы счисления делятся на два типа: непозиционный и позиционный. В непозиционных системах счисления значение любого символа не зависит от его положения (позиции) в ряду символов, изображающих это число. Например римская система, в которой в числе ХХХ каждый символ Х означает 10 единиц. В позиционных системах счисления значение любого символа зависит от занимаемой символом позиции в изображении числа. Она является основной в ЦВМ. Позиционные системы счисления включают определенное количество символов (основание системы счисления), используемых для изображения числа. Основание системы счисления N показывает, во сколько раз «вес» i-го разряда больше (i-1) разряда. Целая часть числа отделяется от дробной части точкой (запятой) Теоретически, наиболее экономичной системой счисления является система с основанием е = 2,71828..., находящимся между числами 2 и 3. Во всех современных ЭВМ для представления числовой информации используется двоичная система счисления (при N=2 число различных символов, используемых для записи чисел, ограничено мощностью множества из двух символов: нуль и единица). Приоритет выбора двоичной системы счисления обусловлен: - более простой реализацией алгоритмов выполнения арифметических и логических операций; - более надежной физической реализацией основных функций, так как они имеют всего два состояния («0» и «1»); - экономичностью аппаратурной реализации всех схем ЭВМ.
Кроме двоичной системы счисления широкое распространение получили и производные системы: • восьмеричная - {0,1,2,3,4,5,6,7}. Она широко используется во многих специализированных ЭВМ. • шестнадцатеричная - {0,1,2,...9, А, В, С, D, Е, F}. Здесь символ шестнадцатеричной системы счисления «А» обозначает десятичное число 10, «В» - число 11,..., «F» - число 15; • двоично-десятичное представление десятичных чисел четырехразрядными двоичными кодами - тетрадами, - {О, 1.....9}. Восьмеричная и шестнадцатеричная системы счисления являются производными от двоичной, так как 8 = 23 и 16 = 24. Они используются в основном для более компактного изображения двоичной информации, так как запись значения чисел производится существенно меньшим числом знаков. В позиционных системах каждая символ числа имеет определенный вес, зависящий от позиции символа в последовательности, изображающей число. Позиция символа называется разрядом. В позиционной системе счисления любое число можно представить в виде полинома: A n = a m-1 N m-1+ a m-2 N m-2 +…+ a 1 N 1 + a 0 N 0+…+ a -1 N -1+ a -k N -k (2.1) A n = å a i N i где а - i-я цифра числа; k - количество цифр в дробной части числа; т - количество цифр в целой части числа; N - основание системы счисления. Свернутая форма представления чисел имеет вид: An = a m-1 a m-2… a i a 0 · a -1 a -2… a -k (2.2)
908,81 Числа в системах счисления
Например, символ шестнадцатеричной системы счисления D равен числу 13 в десятичной системе счисления. Единица старшего разряда представляется тетрадой 0001, а тройка младшего разряда – тетрадой 0011. Таким образом, запись двоично-кодированного числа равна 00010011(2/10). Представление чисел в различных системах счисления допускает однозначное преобразование их из одной системы в другую. В ЭВМ перевод из одной системы в другую осуществляется автоматически по определенным правилам. Правила перевода целых и дробных чисел отличаются. Правило 1. Для перевода целого десятичного числа в систему счисления с основанием N надо переводимое число последовательно делить на это основание N новой системы счисления, (в которую это число переводится), до тех пор, пока не будет получено частное, меньшее основания N. Число в новой системе счисления запишется цифрами новой системы счисления в виде остатков от деления в порядке обратном, полученному при делении, начиная с последнего частного, представляющего собой старшую цифру числа. Пример 1.1. Перевести Пример 1.2. Перевести Пример 1.3. Перевести число 54(10) в двоичную число 348(10) в восьме- число 875(10) в шестнад- систему счисления. ричную систему счисл. цатеричную сист.счисл Решение. Решение. Решение. _54 2 _348 8 _875 16 54 _27 2 344 _43 8 864 _54 16
1 6 _3 2 0 2 1 11(10) = B(16)
т.е. 54(10)=110110(2). т.е. 348(10)=534(8). т.е. 875(10)=35В(16).
Правило 2. Для перевода правильных десятичных дробей в систему счисления с основанием N умножают исходную дробь последовательно на основание новой системы счисления N (целые части дроби в процедуре умножения не участвуют). Полученные в результате умножения целые части произведения, записанные цифрами новой системы счисления, являются соответствующими разрядами дробного числа в новой системе счисления с основанием N. Число умножений определяет разрядность полученного результата, представляющего исходную правильную дробь в системе счисления N.
Пример 1.4. Перевести Пример 1.5. Перевести Пример 1.6. Перевести число 0,725(10) в двоичную число 0,873(10) в восьме- число 0,27(10) в шестна- систему счисления. ричную систему счисления дцатеричную систему счисления Решение. Решение. Решение.
1, 450 6, 696 4, 32 х 2 x 8 x 16 0, 90 5, 568 5, 12 х 2 x 8 x 16 1, 8 4, 548 1, 92 х 16 14,72 т.е. 0,725(10) = 0,101 (2) т.е. 0,873(10) = 0,654 (8) т.е. 0,27(10) = 0.451Е (16)
Перевод неправильных десятичных дробей в систему счисления с основанием N выполняется отдельно для целой и дробной частей числа по вышеизложенным правилам. Затем эти части соединяются в одну запись - неправильную дробь, представленную уже в новой системе счисления. Правило 3. Перевод числа из любой системы счисления в десятичную осуществляется представлением этого числа в развернутом виде, а именно - суммы степеней основания, умноженных на цифры переводимого числа, т.е. в виде полинома. При этом все арифметические действия осуществляются в десятичной системе счисления, а цифры переводимого числа считаются десятичными. В качестве примеров воспользуемся числами 175,61(8), 1101,11(2), A1F,96(16). Пример 1.7. 175,61(8) = 1х82 + 7х81 +5х80 +6х8-1 + 1х8-2 = = 64 + 56 + 5 + 0,75 + 0,015625 = 12,765625(10); Пример 1.8. 1101,11(2) = 1х23 + 1х22 + 0х21 +1х20 +1х2-1 + 1х2-2 = = 8 + 4 + 0 + 1 + 0,5 + 0,25 = 13,75(10); Пример 1.9. A1F,96(16) = Ах162 + 1х161 + Fх160 + 9х16-1 + 6х16-2 = = 2560 + 16 + 1 + 0,625 + 0,0234375 = 2591,6484(10). Частные правила перевода
Так как двоичная, восьмеричная и шестнадцатеричная системы связаны через степени числа 2, то преобразования между ними можно выполнять другим более простым способом. Для перевода из шестнадцатеричной (восьмеричной) системы счисления в двоичную достаточно двоичным кодом записать шестнадцатеричные символы тетрадами (по 4 двоичных разряда) и триадами (по 3 двоичных разряда) - для восьмеричных символов. Обратный перевод из двоичного кода производится в обратном порядке: двоичное число разбивается влево и вправо от границы целой и дробной частей на тетрады - для последующей записи символов в шестнадцатеричном представлении, на триады - для записи их значений восьмеричными символами. Пример 1.10. Перевести число 67532.107(8) в двоичную систему счисления. Решение. Заменить каждый символ трехзначным двоичным кодом: 6 7 5 3 2. 1 0 7 110 111 101 011 010 001 000 111 т.е. 67532.107(8) = 110111101011010.001000111(2). Перевод чисел из двоичной системы счисления в восьмеричную осуществляется заменой каждой триады одноразрядным символом восьмеричной системы счисления (причем, триады формируются влево и вправо от точки). При смешанных числах (неправильная дробь) триады слева и справа дополняются нулями в случае, если не хватает цифр до полной триады. Пример 1.11. Перевести число 10111011101. 1101(2) в восьмеричную систему счисления. Решение. Заменить каждую триаду восьмеричным числом: 010 111 011 101. 110 100 2 7 3 5. 6 4 т.е. 10111011101. 1101(2) = 2735. 64(8). Для перевода неправильной дроби из шестнадцатеричной системы счисления в двоичную каждый шестнадцатеричный символ заменяют его двоичным эквивалентом, т.е. четырьмя двоичными символами (тетрадой).
Пример 1.12. Перевести число 35В,451Е(16) в двоичную систему счисления. Решение. Заменить каждый шестнадцатеричный символ двоичной тетрадой: 3 5 В. 4 5 1 Е 0011 0101 1011, 0100 0101 0001 1110 т.е.. 35В.451Е(16) = 001101011011.0100010100011110(2). Перевод неправильной дроби из двоичной системы счисления в шестнадцатеричную осуществляется по тем же правилам, что и перевод чисел из двоичной системы счисления в восьмеричную, с той только разницей, что число в двоичной системе счисления разбивается на тетрады влево и вправо от запятой и каждая тетрада заменяется символом шестнадцатеричной системы счисления.
Машинные коды чисел. Различают прямой код (ПК), обратный код (ОК) и дополнительный код (ДК) двоичных чисел. Прямой код двоичного числа образуется из абсолютного значения этого числа и кода знака (нуль или единица) перед его старшим числовым разрядом. Пример 1.13. A 10 = +10 A 2 = +1010 [ A 2]пк = 0. 1010; В 10 = -13 В 2 = - 1101 [ В 2]пк = 1. 1101; Точкой здесь отмечена условная граница, отделяющая знаковый разряд от значащих. Обратный код двоичного числа образуется по следующему правилу. Обратный код положительных чисел совпадает с их прямым кодом. Обратный код отрицательного числа содержит единицу в знаковом разряде числа, а значащие разряды числа заменяются на инверсные, т.е. нули заменяются единицами, а единицы - нулями. Пример 1.14. A 10 = +10 A 2 = +1010 [ A 2]пк = 0.1010 [ A 2]ок = 0.1010; В 10 = -13 В 2 = - 1101 [ В 2]пк = 1.1101 [ В 2]ок = 1.0010; Укажем наиболее важные свойства обратного кода чисел: • сложение положительного числа С с его отрицательным значением в обратном коде дает так называемую машинную единицу МЕок = 1.111... 11, состоящую из единиц в знаковом и значащих разрядах числа; • нуль в обратном коде имеет двоякое значение. Он может быть положительным – 0.00...0 и отрицательным числом – 1.11... 11. Значение отрицательного нуля совпадает с МЕок. Двойственное представление нуля явилось причиной того, что в современных ЭВМ все числа представляются не обратным, а дополнительным кодом. Дополнительный код положительных чисел совпадает с их прямым кодом. Дополнительный код отрицательного числа представляет собой результат суммирования обратного кода числа с единицей. Пример 1.15. A 10 = +10 A 2 = +1010 [ A 2]пк = 0.1010 [ A 2]ок = 0.1010 [ A 2]дк = 0.1010; В 10 = -13 В 2 = - 1101 [ В 2]пк = 1.1101 [ В 2]ок = 1.0010 [ В 2]дк = 1.0011; Укажем основные свойства дополнительного кода: • сложение дополнительных кодов положительного числа А с его отрицательным значением дает так называемую машинную единицу дополнительного кода: Медк = МЕок+20 =10.00...00, т.е. число 10 (два) в знаковых разрядах числа; • дополнительный код получил такое свое название потому, что представление отрицательных чисел является дополнением прямого кода чисел до машинной единицы МЕдк. Модифицированные обратные и дополнительные коды двоичных чисел отличаются соответственно от обратных и дополнительных кодов удвоением количества знаковых разрядов. Знак «+» в этих кодах кодируется двумя нулевыми знаковыми разрядами, а «-» - двумя единичными разрядами. Пример 1.16. A 10 = 9 A 2 = +1001 [ A 2]пк = [A2]ок = [A2]дк = 0.1001; [ A 2]мок = [ A 2]мдк = 00.1001 В 10 = -9 В 2 = - 1001 [ В 2]ок = 1.0110 [ В 2]дк = 1.0111 [ B 2]мок = 11.0110 [ B 2]мдк = 11.0111. Целью введения модифицированных кодов являются фиксация и обнаружение случаев переполнения разрядной сетки ЭВМ т.е. получения неправильного результата, когда значение результата превышает максимально возможный результат в отведенной разрядной сетке машины. В этом случае перенос из значащего разряда может исказить значение младшего знакового разряда. Значение знаковых разрядов «01» свидетельствует о положительном переполнении разрядной сетки, а «10» - об отрицательном переполнении. В настоящее время практически во всех моделях ЭВМ роль удвоенных разрядов для фиксации переполнения разрядной сетки играют переносы, идущие в знаковый и из знакового разряда. Пример 1.22. Сложить 2 числа: А=-5 и В=-6 в четырехразрядной сетке (с учетом знакового разряда). Сложение в OK Сложение в ДК [А2]ок = 1.010 [A2] = 1.011 +[В2]ок = 1.011 +[B2] = 1.100 10.101 10.111 0.110 C2 = 0.110 С2 = 0.111 C10 = +6??? (вместо -11)! C10 = +7??? (вместо -11)! Как видно из примеров, при сложении положительных чисел получается отрицательный результат и наоборот. Это объясняется тем, что в трех значащих разрядах максимальное число по модулю может быть семь, а в примерах необходимо записать соответственно С=+11 и С=-11.
Задания для работы на занятии: 1. Перевести из десятичной системы счисления в двоичную, восьмеричную, шестнадцатеричную и двоично-десятичную числа: -175,34; -256,75. 2. Перевести из двоичной системы счисления в десятичную, восьмеричную, шестнадцатеричную и двоично-десятичную числа: -10000111010101,1001; -1111100010101111100101,10101. 3. Образовать все виды машинных кодов от чисел: 35 и -44. Выполнить их сложение во всех кодах и проверить правильность результата. 4. Умножить в машинных кодах числа: -5 и +9; -3 и –8. Результат проверить. 5. Представить числа 35 и –44 в форме с плавающей запятой и показать их размещение в шестнадцатиразрядной сетке ЭВМ. Выполнить сложение в форме с плавающей запятой. Проверить правильность результата.
Контрольные вопросы:
1. Что понимается под системой счисления? 2. Сформулируйте правила перевода целых и дробных чисел из одной системы счисления в другую? 3. Как переводятся числа в системах счисления с основаниями, кратными степени 2? 4. Каково назначение обратного и дополнительного кодов? 5. Каково назначение модифицированных обратного и дополнительного кодов?
Задание на самоподготовку: 1. Составить и выполнить по одному примеру на решение задач по · переводу чисел из одной системы счисления в другую; · образованию машинных кодов; · их сложению, вычитанию и умножению. 2. Подготовиться к ПЗ№2 "Минимизация логических функций".
Литература: 1. Пятибратов А.П. и др. Вычислительные системы, сети и телекоммуникации: Учебник.-2-е изд., перераб. и доп./ А.П.Пятибратов, Л.П. Гудыно, А.А.Кириченко; Под ред. А.П.Пятибратова. М.: Финансы и статистика, 2002.-512с:ил. 2. Каган Б.М. Электронные вычислительные машины и системы: Учеб. Пособие для вузов.-3-е изд.,перераб и доп.-М.: Энергоатомиздат,1991.-592с.:ил. 3. Нешумова К.А. Электронные вычислительные машины и системы. М.: Высшая школа, 1989.-366с.:ил.
Теоретические сведения РАСЧЕТНЫЙ МЕТОД Пусть нам требуется минимизировать ФАЛ, заданную выражением (2.1). 1 этап. Выполняем операции склеивания конституент единицы. Для упорядочения этой процедуры запишем выражение (2.1) в виде нескольких строк по следующему правилу: первая строка — это исходное уравнение, вторая строка — вторая конституента и все последующие, третья строка — третья конституента и все последующие и т. д. Это допустимо, так как в булевой алгебре действует закон тавтологии.
+ х2х1х0 +х2х1х0 + х2х1х0 + х2х1х0 + х2х1х0 + х2х1х0 (2.7) Производится проверка на склеивание первого члена в каждой строке со всеми остальными в данной строке. В первой строке склеиваются первая и третья конституенты, во второй — первая со второй и четвертой, в третьей первая конституента с остальными не склеивается, и в последней строке конституенты склеиваются. Поскольку все конституенты участвовали хотя бы в одном склеивании, то в СокрДНФ ни одной конституенты не будет. После этой процедуры получаем следующее выражение:
Дальнейшее склеивание не может быть выполнено, так как все члены выражения (2.8) являются изолированными. 2 этап. Необходимо выявить лишние импликанты в выражении (2.8). Это можно сделать двумя способами.
Y= х2х0 + х2х1 + х2х0 (2.10) 3 этап. Выражение (9) можно записать в виде: Y= х2х0 + (х2+х1)х0 (2.11) Оно содержит 5 букв и требует 3 инвертора. Применив закон двойного отрицания и правило де Моргана, выражение (11) можно преобразовать:
Y= х2х0 + (х2+х1)х0 = х2х0 + х2х1х0 (2.12) Последнее выражение содержит 5 букв и требует 2 инвертора. Аналогично можно упростить и выражение (2.10): у = х2(x1 + х0) + х2x0 = х2 х1х0+ х2x0, (2. 13 ) Второй способ выявления лишних импликант заключается в следующем. На значение истинности функции влияет только та импликанта, которая сама равна 1. Любая импликанта принимает значение 1 только на одном наборе своих аргументов. Но, если именно на этом наборе сумма остальных импликант также обращается в 1, то рассматриваемая импликанта не влияет на значение истинности функции даже в этом единственном случае, то есть является лишней. Применим это правило к выражению (2.8). Импликанта х2x0, принимает значение 1 на наборе х2 = 1, х0 = 0. Подставив этот набор в оставшуюся сумму х2х1 + х1х0,+ х2х0, получим х1 что говорит о том, что первая импликанта не является лишней. Импликанта х2х1, принимает значение 1 на наборе х2 = 1, х1 = 0. Подставив этот набор в сумму х2х0+х1х0+х2х0, получим х0 + х0 = 1, что говорит о том, что импликанта х2х1 — лишняя. Оставим пока эту импликанту и продолжим анализ других. Импликанта х1х0 принимает значение 1 на наборе х1 = 0, х0 = 1. Подставив этот набор в сумму х2х0+ х2х1 +х2х0, получим х2 + х2 = 1, что говорит о том, что импликанта х1х0— лишняя. Оставляем и ее и продолжаем процедуру. Импликанта х2х0, принимает значение 1 на наборе х2= 0, х0= 1. Подставив этот набор в сумму х2х0 + х2х1 + х1х0, получаем х1 , что говорит о том, что импликанта х2х0 не является лишней. Как и в первом случае, нельзя отбрасывать обе обнаруженные лишние импликанты, так как каждая из них проверялась при вхождении второй в оставшуюся сумму. Опустим рассмотрение дальнейших шагов — они аналогичны процедурам, выполненным первым способом. Можно сделать вывод, что даже для этого простого примера пришлось выполнять достаточно много однообразных действий, требующих внимания и времени, поэтому расчетный метод минимизации применяется, в основном, для ФАЛ, зависящих от 2 или 3 переменных. ТАБЛИЧНЫЙ МЕТОД При этом методе два первых этапа выполняются при помощи специальных карт, впервые предложенных Вейтчем и модернизированных Карно. Практическое применение получили именно карты Карно, а не диаграммы Вейтча, и хотя с момента опубликования их оригинальных работ прошло 45 лет, до сих пор многие авторы называют карты Карно диаграммами Вейтча. Поскольку сами эти работы — библиографические редкости, и их можно найти только в крупнейших библиотеках, приведем цитату из работы [2]: "Матрица Вейтча отличается от матрицы Карно расположением столбцов и строк. В то время как Карно пользуется циклическим порядком следования символов, а именно 00, 01, 11, 10, Вейтч располагает символы в порядке возрастания двоичных чисел, а именно 00, 01, 10, 11. Столбцы или строки 00 и 01, так же как столбцы или строки 10 и 11, являются в матрице Вейтча соседними, но столбцы или строки 01 и 10 в ней не являются ни соседними, ни крайними. Хотя матрица Вейтча и обладает некоторыми преимуществами по сравнению с алгебраическими методами, матрица Карно более удобна в обращении и не требует столь большой затраты времени". Итак, табличный метод минимизации ФАЛ — это метод, основанный на использовании карт Карно. Карта Карно — специальная форма таблицы истинности ФАЛ, позволяющей не только задать ФАЛ, но и выполнить первый и второй этапы минимизации. Таблица истинности содержит 2n строк, в которых наборы nпеременных расположены в линейной лексикографической последовательности, а также столбец значений ФАЛ на этих наборах. Напомним, что в таблице истинности переменные с большим весом располагаются на левой позиции набора. Карта Карно содержит 2n клеток (квадратов), расположенных в виде строки (n = 1, 2), либо в виде двумерной матрицы (n >= 2). Каждая клетка, как и строка в таблице истинности, соответствует одному набору. Для того, чтобы можно было производить минимизацию ФАЛ, необходимо в смежных в геометрическом смысле клетках карты расположить соседние наборы. Это можно обеспечить, если наборы переменных, определяющих "координаты" клетки карты Карно, расположить в циклическом коде Грея, у которого каждое следующее значение отличается от предыдущего только в одном разряде. На рис. 2.1 представлена так называемая эталонная карта Карно для n=3. Она служит для указания расположения переменных, как координат клеток, так и наборов этих переменных. Координатой клеток в горизонтальном направлении служат наборы переменных x1x0 ,а координатой клеток в вертикальном направлении служит одна переменная х2. ____________________ Х1
_____________________ Х0 Рис. 2.1. Эталонная карта Карно для n = 3 Известно, что каждая из nпеременных встречается в половине наборов без инверсии, а в другой половине с инверсией. Три линии, расположенные с внешней стороны карты Карно, указывают, что в соответствующих им половинах клеток указанная рядом с этой линией переменная встречается в наборе без инверсии и, соответственно, в другой половине с инверсией. Так как переменным х0,х1,х2 условно присваиваются "веса" соответственно 20 = 1, 21 = 2 и 22 = 4, то 8 наборов в клетках карты Карно будут расположены так, как указано на рис. 2.1. Итак, расположение переменных как координат клеток карты Карно и номеров наборов в эталонной карте должны строго соответствовать друг другу. Можно произвольно поменять местами переменные х0,х1,х2, но тогда обязательно надо поменять местами и расположение наборов. Несмотря на то, что карты Карно изображаются на плоскости, с точки зрения обеспечения соседства их клеток карты нужно считать трехмерными объектами, так как клетки, расположенные на концах одних и тех же строк и столбцов, также являются соседними. Так, карту для 3 переменных следует рассматривать как цилиндр со склеенными правым и левым краями. Карту Карно для 4 переменных (рис. 2.4,а) нужно считать склеенной не только по правому и левому краям, но и по верхнему и нижнему. Таким образом, карта Карно для 4 переменных должна рассматриваться как поверхность тора. Рабочая карта Карно, соответствующая таблице истинности, рассмотренной в примере, будет иметь вид, представленный на рис. 2.2.
__________________ Х1
____________________ Х0 Рис. 2.2. Рабочая карта Карно для ФАЛ, заданной таблицей примера. Буква Y рядом с косой линией, проставляемой обычно в левом верхнем углу карты Карно, обозначает реализуемую функцию, а цифры 0 и 1 в клетках карты указывают значения этой функции на соответствующих наборах. Полученную рабочую карту Карно можно интерпретировать как компактное представление ФАЛ в СДНФ (по значениям истинности) либо в СКНФ (по значениям ложности). Дальнейшее изложение ведется в предположении, что минимизация происходит в дизъюнктивных формах. Процесс минимизации с помощью карт Карно базируется на использовании операции склеивания и основан на следующих положениях: 1. На картах Карно необходимо выделить монолитные (сплошные) области первых клеток, образующих строку, столбец, прямоугольник или квадрат и содержащих 1, 2, 4, 8 и т. д. клеток. Эти выделенные области (или контуры покрытия) будут соответствовать импликантам. Очевидно, что одна изолированная первая клетка будет соответствовать конституенте единицы. Две смежные клетки будут соответствовать ' импликанте, ранг которой r = n-1, четыре смежные клетки - импликанте с рангом r = n - 2и т. д. 2. Переменные, от которых импликанта не зависит, входят в соответствующий выделенный контур как в виде хi, так и в виде хi, а остальные переменные только либо в виде хi, либо в виде хi, 3. На основании закона тавтологии любая первая клетка может быть включена в любое число различных контуров. 4. Для получения минимальных ТДНФ в карте Карно не должно быть лишних покрытий, то есть каждую первую клетку достаточно использовать хотя бы один раз. 5. Существуют эквивалентные покрытия для получения различных минимальных ТДНФ. 6. Существуют функции, для которых СДНФ совпадает с минимальной ТДНФ (в этом случае на карте Карно все первые клетки изолированные). 7. Если в карте Карно нет ни одной 1, то ФАЛ эквивалентна константе 0; если нет ни одного 0, то константе 1; если единицы занимают половину клеток карты Карно и представляют из себя монолитный массив в виде строки, столбца, прямоугольника или квадрата, то соответствующая импликанта состоит из одной переменной со знаком или без знака инверсии. С учетом сказанного на картах Карно рис. 2.3 можно выделить три контура, содержащих по две 1. Два варианта покрытия обусловлены тем, что 1 в клетке с набором 5 может образовать контур из двух клеток либо с набором 4
____________________ Х1
_____________________ Х0 а) ____________________ Х1
_____________________ Х0 б) Рис. 2.3. Рабочие карты Карно с двумя эквивалентными покрытиями (рис. 2.З,а), либо с набором 1 (рис. 2.3,6). Поясним получение импликанты для контура, образованного двумя клетками в нижней строке карты. Переменная х2, входит в этот контур только с инверсией, переменная х1, входит в этот контур и с инверсией и без нее, поэтому по ней осуществляется склеивание и она исчезает, переменная х0, входит в этот контур только без инверсии, поэтому импликанта имеет вид х2х0. Для выявленных двух покрытий можно записать
Y= x2x0 + x2x0 + x1x0 (2.15) Простота получения уравнений (2.14) и (2.15) показывает существенное преимущество табличного метода карт Карно перед расчетным методом.
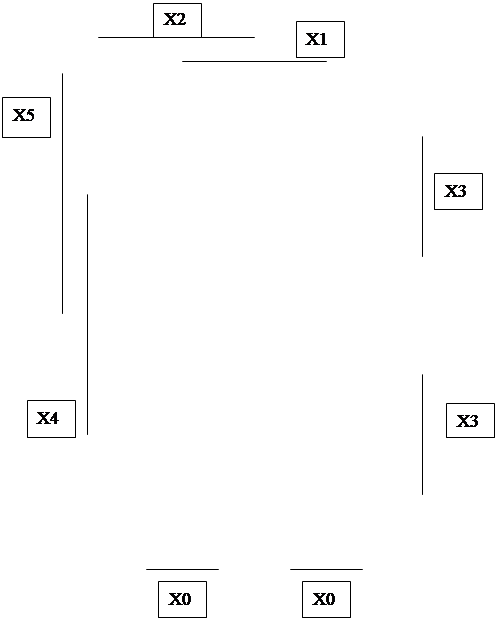
а)
б)
в) Рис. 2.4. Эталонные карты Карно для n=4,5,6. На рис. 2.4 показаны эталонные карты Карно для n=4,5,6. Причем для n=5 и 6 можно рассматривать их как две и четыре карты Карно для n=4, имеющие общие границы, проведенные по осям симметрии, разделяющим их на карты для случая n=4. Эти составные части называют соседними картами Карно. Правила соседства для какой-либо клетки в этом случае выглядит так: для любой выделенной клетки соседними являются ч
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 572; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.33 (0.018 с.) |

 Крайняя правая цифра любого числа называется его младшим, или наименьшим, значащим разрядом, а крайняя левая - старшим, или наибольшим, значащим разрядом. Например,
Крайняя правая цифра любого числа называется его младшим, или наименьшим, значащим разрядом, а крайняя левая - старшим, или наибольшим, значащим разрядом. Например,

 0 26 _13 2 4 40 5 11 48 3
0 26 _13 2 4 40 5 11 48 3

 1 12 _6 2 3 5
1 12 _6 2 3 5 1
1
 х 2 x 8 x 16
х 2 x 8 x 16
 У = х2х1х0 + х2х1х0 + х2х1х0 + х2х1х0 + х2х1х0 + х2х1х0 + х2х1х0 + х2х1х0 +
У = х2х1х0 + х2х1х0 + х2х1х0 + х2х1х0 + х2х1х0 + х2х1х0 + х2х1х0 + х2х1х0 + у = х2х0 + х2х1 + х1х0,+ х2х0 (2.8)
у = х2х0 + х2х1 + х1х0,+ х2х0 (2.8) При первом развертывают одну импликанту до конституент единицы, а затем смотрят, не поглощаются ли эти конституенты остальными импликантами. Первая импликанта развертывается до суммы х2х0 = х1&1&х0 = х2(х1+х1)х0= x2x1x0 + x2x1x0, причем конституента x2x1x0 не поглощается ни одной импликантой, следовательно, импликанта x2x0 не является лишней. Вторая импликанта x2x1, развертывается до суммы x2x1x0 + x2x1x0 , причем обе конституенты поглощаются остальными импликантами, следовательно, импликанта x2x1 — лишняя. Продолжим эту процедуру, оставив пока импликанту x2x1 в выражении (8). Импликанта x1x0 развертывается до суммы x2x1x0 + x2x1x0, причем обе конституенты поглощаются остальными импликантами, следовательно, импликанта x1x0 — лишняя. Продолжим, оставив в выражении (2.8) и эту импликанту. Развертывание последней импликанты дает сумму x2x1x0 + x2x1x0, в которой конституента x2x1x0 , не поглощается ни одной импликантой, следовательно, импликанта x2x0 ,не является лишней. Выявлены две лишние импликанты, но это не значит, что обе они могут быть отброшены, так как каждая из них проверялась при вхождении второй в выражение (2.8). Следовательно, отбросить наверняка можно одну из них, а затем снова произвести проверку возможности отбросить и другую. Если отбросить импликанту x2x1, то проверка показывает, что импликанта x1x0 не будет лишней, а если отбросить x1x0 , то x2x1, не будет лишней. Итак, можно отбросить одну из выявленных двух импликант. В результате получаются две ТДНФ одинаковой сложности, содержащих по 6 букв:
При первом развертывают одну импликанту до конституент единицы, а затем смотрят, не поглощаются ли эти конституенты остальными импликантами. Первая импликанта развертывается до суммы х2х0 = х1&1&х0 = х2(х1+х1)х0= x2x1x0 + x2x1x0, причем конституента x2x1x0 не поглощается ни одной импликантой, следовательно, импликанта x2x0 не является лишней. Вторая импликанта x2x1, развертывается до суммы x2x1x0 + x2x1x0 , причем обе конституенты поглощаются остальными импликантами, следовательно, импликанта x2x1 — лишняя. Продолжим эту процедуру, оставив пока импликанту x2x1 в выражении (8). Импликанта x1x0 развертывается до суммы x2x1x0 + x2x1x0, причем обе конституенты поглощаются остальными импликантами, следовательно, импликанта x1x0 — лишняя. Продолжим, оставив в выражении (2.8) и эту импликанту. Развертывание последней импликанты дает сумму x2x1x0 + x2x1x0, в которой конституента x2x1x0 , не поглощается ни одной импликантой, следовательно, импликанта x2x0 ,не является лишней. Выявлены две лишние импликанты, но это не значит, что обе они могут быть отброшены, так как каждая из них проверялась при вхождении второй в выражение (2.8). Следовательно, отбросить наверняка можно одну из них, а затем снова произвести проверку возможности отбросить и другую. Если отбросить импликанту x2x1, то проверка показывает, что импликанта x1x0 не будет лишней, а если отбросить x1x0 , то x2x1, не будет лишней. Итак, можно отбросить одну из выявленных двух импликант. В результате получаются две ТДНФ одинаковой сложности, содержащих по 6 букв: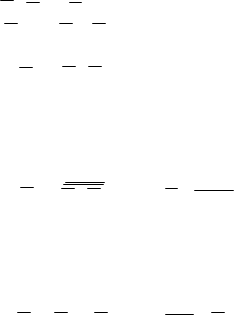 Y=х2х0+х1х0+х2х0 (2.9)
Y=х2х0+х1х0+х2х0 (2.9)

 Y
Y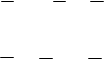 Y= x2x1 + x2x0 + x2x0 (2.14)
Y= x2x1 + x2x0 + x2x0 (2.14)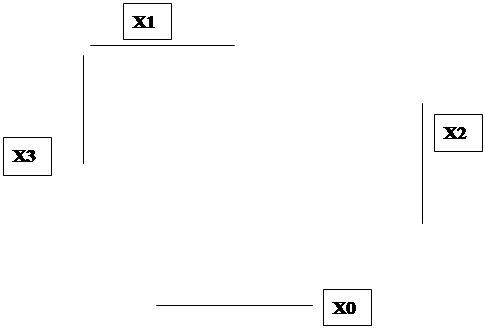

 42
42



