
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Минимизация функций алгебры логикиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Проблема минимизации логических функций решается на основе применения законов склеивания и поглощения с последующим перебором получаемых дизъюнктивных форм и выбором из них оптимальной (минимальной). Существует большое количество методов минимизации ЛФ. Все они отличаются друг от друга спецификой применения операций склеивания и поглощения, а также различными способами сокращения переборов.
Минимизация функций алгебры логики (ФАЛ) – это процедура нахождения наиболее простого представления ФАЛ в виде суперпозиции функций, составляющих функционально полную систему, при одновременной оптимизации ее схемотехнической реализации по некоторым критериям в условиях ряда ограничений. Критериями оптимизации могут быть объем оборудования (количество вентилей, корпусов и т.п.), вес, габариты, стоимость, быстродействие и другие. В качестве ограничений могут использоваться допустимые к применению системы элементов, число элементов в корпусе, коэффициенты объединения по входу и разветвления по выходу логических элементов и т.д. Решение задачи минимизации в полном объеме представляет трудную проблему поскольку ряд критериев оптимизации зачастую находится в противоречии друг с другом. Поэтому зачастую задачу минимизации решают в упрощенной постановке, например, ограничиваются задачей представления ФАЛ в дизъюнктивной или конъюнктивной форме, содержащей наименьшее возможное число логических переменных (букв в формуле ФАЛ). Каноническая задача минимизации формулируется так: · Для пояснения сказанного рассмотрим пример представления ФАЛ, заданной следующей таблицей истинности.
ФАЛ, заданную таблицей истинности, можно представить следующими выражениями:
Y= X2 X1 + X2 X0 + X2 X0 (2.2) Y =(Х2 +Х1 + X0) (Х2 +Х1 + X0) (Х2 +Х1 + X0) (2.3) Y =(Х2 + X0) (Х2 +Х1 + X0) (2.4) В выражении (1), записанном в СДНФ, 5 слагаемых по 3 буквы в каждом, а всего 15 букв и 3 инвертора, в то время как в выражении (2.2) 3 слагаемых по 2 буквы в каждом, а всего 6 букв и 3 инвертора. Выражение (2.2) является минимальной дизъюнктивной формой для данной ФАЛ. В выражении (2.3), записанном в СКНФ, 3 сомножителя по 3 буквы в каждом, а всего 9 букв и 3 инвертора, в то время как в выражении (2.4) 2 сомножителя по 2 и 3 буквы, а всего 5 букв и 3 инвертора. Выражение (2.4) — минимальная конъюнктивная форма для данной ФАЛ. Применяя скобочные формы и формы с групповыми инверсиями, выражения (2.2) и (2.4) можно еще упростить:
где 5 букв и 2 инвертора. Y=(Х2 + X0)(Х2 + Х1 + X0) = (Х2 +X0) Х2Х1X0 (2.6) где 5 букв и 1 инвертор. В настоящее время в теории проектирования логических схем наиболее полно исследованы именно задачи минимизации дизъюнктивных и конъюнктивных нормальных форм, обеспечивающих рациональное решение при синтезе комбинационных схем, на входах которых доступны как переменные, так и их инверсии. Такое парафазное представление переменных легко обеспечивается, если они снимаются с выходов триггеров, используемых в качестве запоминающих элементов разрабатываемых цифровых устройств. Сформулированная выше задача минимизации ФАЛ являлась чрезвычайно актуальной в тот период времени, когда разработка цифровых устройств велась на электромеханических переключательных элементах, дискретных радиокомпонентах и интегральных схемах малой степени интеграции. Достигнутые в настоящее время схемотехнологические успехи в микроэлектронике, в частности создание схем средней, большой и сверхбольшой интеграции таких как мультиплексоры, постоянные запоминающие устройства (ПЗУ), программируемые логические матрицы (ПЛМ) и другие разновидности программируемых логических интегральных схем, позволяют реализовать очень сложные системы ФАЛ, используя, практически, один корпус без каких-либо процедур минимизации. Например, используя ПЗУ типа КР556РТ16 или К1623РТ2 с организацией 8Кх8, можно реализовать систему восьми ФАЛ, зависящих от 13 переменных. Учитывая, что такие БИС дороги, требуют сложной anпаратно-программной поддержки для их программирования, а в инженерной практике чаще решаются более простые задачи, рассмотрим вопросы минимизации ФАЛ, остановившись на некоторых, нашедших наибольшее распространение, методах минимизации ФАЛ. К настоящему времени широкое применение получили: 1. Расчетный метод (метод непосредственных преобразований). 2. Расчетно-табличный метод (метод Квайна-Мак Класки).
4. Табличный метод (карты Карно). 5. Метод гиперкубов. 6. Метод факторизации. 7. Метод функциональной декомпозиции и др. Первый метод применяется при числе переменных n <= 3 и основан на использовании операций склеивания, поглощения и развертывания. Ниже он будет рассмотрен подробно. Второй и третий методы используются при п<=16 в профессиональных разработках и ориентированы на использование САПР с применением ЭВМ. Здесь они рассматриваться не будут. Четвертый метод является самым распространенным инженерным методом минимизации ФАЛ для n<=6 и будет рассмотрен подробно. Шестой метод не имеет каких-либо существенных достижений при решении общих задач, более простых, чем метод перебора всех формул ФАЛ даже для n = 3. Практически он применяется для уменьшения сложности минимальных ДНФ и КНФ, полученных с помощью первого или четвертого методов. Он основан на использовании скобочных форм и форм с групповыми инверсиями. Седьмой метод представляет ФАЛ, зависящую от nпеременных, в виде суперпозиций функций, зависящих от меньшего числа переменных, для которых можно применить вышеперечисленные методы, и здесь не рассматривается. Исходной формой для большинства методов являются либо таблица истинности, либо одна из совершенных форм - СДНФ или СКНФ. Если ФАЛ задана в другом виде, то предполагается, что она сначала переводится в СДНФ или СКНФ с использованием основных законов булевой алгебры. Далее будут рассмотрены методы минимизации ФАЛ, представленной в СДНФ. При выполнении процедур канонической минимизации большую роль играют понятия импликанты и простой импликанты ФАЛ. Булева функция z = f1(xn-1; xn-2;...; x0) называется импликантой булевой функции Y = f2(xn-1; xn-2;...; x0), если на любом наборе значений переменных xn-1; xn-2;...; x0, на котором значение функции zравно 1, значение функции Y также равно 1. Простой импликантой функции Y называется всякое элементарное произведение z = xn-1; xn-2;...; x0, являющееся импликантой функции, такое, что никакая его собственная часть (то есть произведение, полученное из произведения z выбрасыванием одного или нескольких сомножителей xi) уже не является импликантой функции Y. Так как в дальнейшем будут использоваться только простые импликанты, опустим слово "простые", то есть если в тексте встречается понятие "импликанта", то надо помнить, что имеется в виду простая импликанта. В общем случае минимизация ФАЛ, заданной в СДНФ, требует выполнения процедур следующих трех этапов. 1 этап — переход от СДНФ к сокращенной ДНФ (СокрДНФ). СокрДНФ — это форма ФАЛ, членами которой являются изолированные (несклеивающиеся) элементарные произведения. Этот этап основан на выполнении всех возможных склеиваний друг с другом сначала конституент единицы, а затем произведений меньшего ранга (импликант). Отметим, что существуют ФАЛ, у которых СДНФ совпадает с СокрДНФ. 2 этап — переход от СокрДНФ к тупиковой ДНФ (ТДНФ). ТДНФ — это форма ФАЛ, членами которой являются импликанты, среди которых нет ни одной лишней. Лишней импликантой называется член ФАЛ, удаление которого из выражения не изменяет ФАЛ. Отметим, что возможны случаи, когда в СокрДНФ нет лишних импликант. Иногда из одной СокрДНФ можно получить несколько различных ТДНФ. Термин "тупиковая" говорит о том, что дальнейшая минимизация в рамках нормальных форм уже невозможна. 3 этап — переход от ТДНФ к минимальной форме. Этот этап основывается на использовании групповых инверсий и скобочных форм, не является систематическим и во многом определяется опытом разработчика. РАСЧЕТНЫЙ МЕТОД Пусть нам требуется минимизировать ФАЛ, заданную выражением (2.1). 1 этап. Выполняем операции склеивания конституент единицы. Для упорядочения этой процедуры запишем выражение (2.1) в виде нескольких строк по следующему правилу: первая строка — это исходное уравнение, вторая строка — вторая конституента и все последующие, третья строка — третья конституента и все последующие и т. д. Это допустимо, так как в булевой алгебре действует закон тавтологии.
+ х2х1х0 +х2х1х0 + х2х1х0 + х2х1х0 + х2х1х0 + х2х1х0 (2.7) Производится проверка на склеивание первого члена в каждой строке со всеми остальными в данной строке. В первой строке склеиваются первая и третья конституенты, во второй — первая со второй и четвертой, в третьей первая конституента с остальными не склеивается, и в последней строке конституенты склеиваются. Поскольку все конституенты участвовали хотя бы в одном склеивании, то в СокрДНФ ни одной конституенты не будет. После этой процедуры получаем следующее выражение:
Дальнейшее склеивание не может быть выполнено, так как все члены выражения (2.8) являются изолированными. 2 этап. Необходимо выявить лишние импликанты в выражении (2.8). Это можно сделать двумя способами.
Y= х2х0 + х2х1 + х2х0 (2.10) 3 этап. Выражение (9) можно записать в виде: Y= х2х0 + (х2+х1)х0 (2.11) Оно содержит 5 букв и требует 3 инвертора. Применив закон двойного отрицания и правило де Моргана, выражение (11) можно преобразовать:
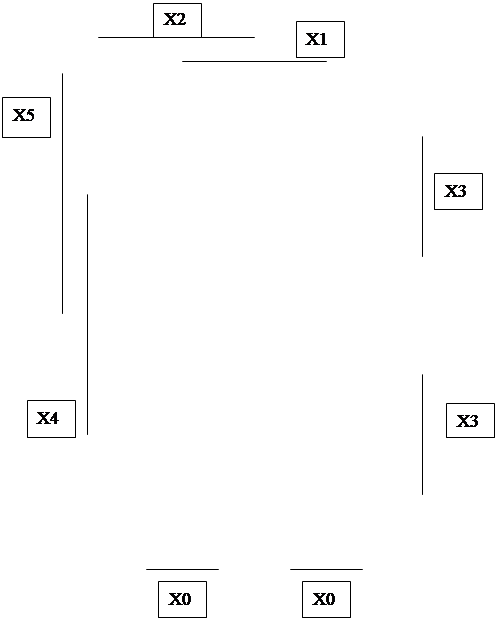
Y= х2х0 + (х2+х1)х0 = х2х0 + х2х1х0 (2.12) Последнее выражение содержит 5 букв и требует 2 инвертора. Аналогично можно упростить и выражение (2.10): у = х2(x1 + х0) + х2x0 = х2 х1х0+ х2x0, (2. 13 ) Второй способ выявления лишних импликант заключается в следующем. На значение истинности функции влияет только та импликанта, которая сама равна 1. Любая импликанта принимает значение 1 только на одном наборе своих аргументов. Но, если именно на этом наборе сумма остальных импликант также обращается в 1, то рассматриваемая импликанта не влияет на значение истинности функции даже в этом единственном случае, то есть является лишней. Применим это правило к выражению (2.8). Импликанта х2x0, принимает значение 1 на наборе х2 = 1, х0 = 0. Подставив этот набор в оставшуюся сумму х2х1 + х1х0,+ х2х0, получим х1 что говорит о том, что первая импликанта не является лишней. Импликанта х2х1, принимает значение 1 на наборе х2 = 1, х1 = 0. Подставив этот набор в сумму х2х0+х1х0+х2х0, получим х0 + х0 = 1, что говорит о том, что импликанта х2х1 — лишняя. Оставим пока эту импликанту и продолжим анализ других. Импликанта х1х0 принимает значение 1 на наборе х1 = 0, х0 = 1. Подставив этот набор в сумму х2х0+ х2х1 +х2х0, получим х2 + х2 = 1, что говорит о том, что импликанта х1х0— лишняя. Оставляем и ее и продолжаем процедуру. Импликанта х2х0, принимает значение 1 на наборе х2= 0, х0= 1. Подставив этот набор в сумму х2х0 + х2х1 + х1х0, получаем х1 , что говорит о том, что импликанта х2х0 не является лишней. Как и в первом случае, нельзя отбрасывать обе обнаруженные лишние импликанты, так как каждая из них проверялась при вхождении второй в оставшуюся сумму. Опустим рассмотрение дальнейших шагов — они аналогичны процедурам, выполненным первым способом. Можно сделать вывод, что даже для этого простого примера пришлось выполнять достаточно много однообразных действий, требующих внимания и времени, поэтому расчетный метод минимизации применяется, в основном, для ФАЛ, зависящих от 2 или 3 переменных. ТАБЛИЧНЫЙ МЕТОД При этом методе два первых этапа выполняются при помощи специальных карт, впервые предложенных Вейтчем и модернизированных Карно. Практическое применение получили именно карты Карно, а не диаграммы Вейтча, и хотя с момента опубликования их оригинальных работ прошло 45 лет, до сих пор многие авторы называют карты Карно диаграммами Вейтча. Поскольку сами эти работы — библиографические редкости, и их можно найти только в крупнейших библиотеках, приведем цитату из работы [2]: "Матрица Вейтча отличается от матрицы Карно расположением столбцов и строк. В то время как Карно пользуется циклическим порядком следования символов, а именно 00, 01, 11, 10, Вейтч располагает символы в порядке возрастания двоичных чисел, а именно 00, 01, 10, 11. Столбцы или строки 00 и 01, так же как столбцы или строки 10 и 11, являются в матрице Вейтча соседними, но столбцы или строки 01 и 10 в ней не являются ни соседними, ни крайними. Хотя матрица Вейтча и обладает некоторыми преимуществами по сравнению с алгебраическими методами, матрица Карно более удобна в обращении и не требует столь большой затраты времени". Итак, табличный метод минимизации ФАЛ — это метод, основанный на использовании карт Карно. Карта Карно — специальная форма таблицы истинности ФАЛ, позволяющей не только задать ФАЛ, но и выполнить первый и второй этапы минимизации. Таблица истинности содержит 2n строк, в которых наборы nпеременных расположены в линейной лексикографической последовательности, а также столбец значений ФАЛ на этих наборах. Напомним, что в таблице истинности переменные с большим весом располагаются на левой позиции набора. Карта Карно содержит 2n клеток (квадратов), расположенных в виде строки (n = 1, 2), либо в виде двумерной матрицы (n >= 2). Каждая клетка, как и строка в таблице истинности, соответствует одному набору. Для того, чтобы можно было производить минимизацию ФАЛ, необходимо в смежных в геометрическом смысле клетках карты расположить соседние наборы. Это можно обеспечить, если наборы переменных, определяющих "координаты" клетки карты Карно, расположить в циклическом коде Грея, у которого каждое следующее значение отличается от предыдущего только в одном разряде. На рис. 2.1 представлена так называемая эталонная карта Карно для n=3. Она служит для указания расположения переменных, как координат клеток, так и наборов этих переменных. Координатой клеток в горизонтальном направлении служат наборы переменных x1x0 ,а координатой клеток в вертикальном направлении служит одна переменная х2. ____________________ Х1
_____________________ Х0 Рис. 2.1. Эталонная карта Карно для n = 3 Известно, что каждая из nпеременных встречается в половине наборов без инверсии, а в другой половине с инверсией. Три линии, расположенные с внешней стороны карты Карно, указывают, что в соответствующих им половинах клеток указанная рядом с этой линией переменная встречается в наборе без инверсии и, соответственно, в другой половине с инверсией. Так как переменным х0,х1,х2 условно присваиваются "веса" соответственно 20 = 1, 21 = 2 и 22 = 4, то 8 наборов в клетках карты Карно будут расположены так, как указано на рис. 2.1. Итак, расположение переменных как координат клеток карты Карно и номеров наборов в эталонной карте должны строго соответствовать друг другу. Можно произвольно поменять местами переменные х0,х1,х2, но тогда обязательно надо поменять местами и расположение наборов. Несмотря на то, что карты Карно изображаются на плоскости, с точки зрения обеспечения соседства их клеток карты нужно считать трехмерными объектами, так как клетки, расположенные на концах одних и тех же строк и столбцов, также являются соседними. Так, карту для 3 переменных следует рассматривать как цилиндр со склеенными правым и левым краями. Карту Карно для 4 переменных (рис. 2.4,а) нужно считать склеенной не только по правому и левому краям, но и по верхнему и нижнему. Таким образом, карта Карно для 4 переменных должна рассматриваться как поверхность тора. Рабочая карта Карно, соответствующая таблице истинности, рассмотренной в примере, будет иметь вид, представленный на рис. 2.2.
__________________ Х1
____________________ Х0 Рис. 2.2. Рабочая карта Карно для ФАЛ, заданной таблицей примера. Буква Y рядом с косой линией, проставляемой обычно в левом верхнем углу карты Карно, обозначает реализуемую функцию, а цифры 0 и 1 в клетках карты указывают значения этой функции на соответствующих наборах. Полученную рабочую карту Карно можно интерпретировать как компактное представление ФАЛ в СДНФ (по значениям истинности) либо в СКНФ (по значениям ложности). Дальнейшее изложение ведется в предположении, что минимизация происходит в дизъюнктивных формах. Процесс минимизации с помощью карт Карно базируется на использовании операции склеивания и основан на следующих положениях: 1. На картах Карно необходимо выделить монолитные (сплошные) области первых клеток, образующих строку, столбец, прямоугольник или квадрат и содержащих 1, 2, 4, 8 и т. д. клеток. Эти выделенные области (или контуры покрытия) будут соответствовать импликантам. Очевидно, что одна изолированная первая клетка будет соответствовать конституенте единицы. Две смежные клетки будут соответствовать ' импликанте, ранг которой r = n-1, четыре смежные клетки - импликанте с рангом r = n - 2и т. д. 2. Переменные, от которых импликанта не зависит, входят в соответствующий выделенный контур как в виде хi, так и в виде хi, а остальные переменные только либо в виде хi, либо в виде хi, 3. На основании закона тавтологии любая первая клетка может быть включена в любое число различных контуров. 4. Для получения минимальных ТДНФ в карте Карно не должно быть лишних покрытий, то есть каждую первую клетку достаточно использовать хотя бы один раз. 5. Существуют эквивалентные покрытия для получения различных минимальных ТДНФ. 6. Существуют функции, для которых СДНФ совпадает с минимальной ТДНФ (в этом случае на карте Карно все первые клетки изолированные). 7. Если в карте Карно нет ни одной 1, то ФАЛ эквивалентна константе 0; если нет ни одного 0, то константе 1; если единицы занимают половину клеток карты Карно и представляют из себя монолитный массив в виде строки, столбца, прямоугольника или квадрата, то соответствующая импликанта состоит из одной переменной со знаком или без знака инверсии. С учетом сказанного на картах Карно рис. 2.3 можно выделить три контура, содержащих по две 1. Два варианта покрытия обусловлены тем, что 1 в клетке с набором 5 может образовать контур из двух клеток либо с набором 4
____________________ Х1
_____________________ Х0 а) ____________________ Х1
_____________________ Х0 б) Рис. 2.3. Рабочие карты Карно с двумя эквивалентными покрытиями (рис. 2.З,а), либо с набором 1 (рис. 2.3,6). Поясним получение импликанты для контура, образованного двумя клетками в нижней строке карты. Переменная х2, входит в этот контур только с инверсией, переменная х1, входит в этот контур и с инверсией и без нее, поэтому по ней осуществляется склеивание и она исчезает, переменная х0, входит в этот контур только без инверсии, поэтому импликанта имеет вид х2х0. Для выявленных двух покрытий можно записать
Y= x2x0 + x2x0 + x1x0 (2.15) Простота получения уравнений (2.14) и (2.15) показывает существенное преимущество табличного метода карт Карно перед расчетным методом.
а)
б)
в) Рис. 2.4. Эталонные карты Карно для n=4,5,6. На рис. 2.4 показаны эталонные карты Карно для n=4,5,6. Причем для n=5 и 6 можно рассматривать их как две и четыре карты Карно для n=4, имеющие общие границы, проведенные по осям симметрии, разделяющим их на карты для случая n=4. Эти составные части называют соседними картами Карно. Правила соседства для какой-либо клетки в этом случае выглядит так: для любой выделенной клетки соседними являются четыре соседние клетки в карте Карно для n=4 и клетки, расположенные в соседних картах Карно и симметрично выделенные относительно границ соседних карт Карно. Например, для клетки 25 на рис.2.4. б) соседними являются клетки 9, 17, 24, 27, 29. Для клетки 2 на рис. 2.4. б) – клетки 0, 3, 6, 10, 18. для клетки 43 на рис 2.4. в) – клетки 11, 35, 41, 42, 47, 59. для клетки 22 на рис 2.4. в) – клетки 6, 18, 20, 23, 30, 54. Задание для работы на занятии 1. Методом непосредственных преобразований минимизировать ФАЛ по варианту, указанному преподавателем.
2. Методом карт Карно проверить правильность результата, полученного при выполнении предыдущего задания.
3. Оценить выигрыш в аппаратных затратах, полученный в результате минимизации ФАЛ.
Вопросы для контроля знаний: 1. С какой целью выполняется минимизация ФАЛ? 2. Перечислить и пояснить основные способы минимизации ФАЛ? 3. Пояснить порядок действий при минимизации ФАЛ расчетным методом? 4. Пояснить порядок действий при минимизации ФАЛ методом Карно? 5. Указать основные достоинства и недостатки метода Карно?
Задание на самоподготовку:
1. Решить две задачи на минимизацию ФАЛ. Условия задачи задать самостоятельно. 2. Подготовиться к ПЗ№3 "Решение задач по синтезу логических схем" Литература 1. Воробьев Н.В. Минимизация функций алгебры логики //Chip News.-1997.- №9-10. –с.54-60. 2. Глушков В.М. Синтез цифровых автоматов.- М.: Физматгиз.-1962.-476с.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 1642; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.011 с.) |

 Минимизация «вручную» возможна только для функций, зависящих от 4-5 переменных, так как трудоемкость переборов растет в квадратичной зависимости от числа переменных. Применение мощных ЭВМ для этих целей позволяет расширить границы до п= 12-15. Если при этом учесть, что функции могут быть частично определены (значения функций на некоторых наборах переменных можно определять произвольно), а также что иногда приходится решать задачи совместной минимизации систем ЛФ, то минимизация ЛФ становится сложной инженерной, практической и научной проблемой.
Минимизация «вручную» возможна только для функций, зависящих от 4-5 переменных, так как трудоемкость переборов растет в квадратичной зависимости от числа переменных. Применение мощных ЭВМ для этих целей позволяет расширить границы до п= 12-15. Если при этом учесть, что функции могут быть частично определены (значения функций на некоторых наборах переменных можно определять произвольно), а также что иногда приходится решать задачи совместной минимизации систем ЛФ, то минимизация ЛФ становится сложной инженерной, практической и научной проблемой. Для дизъюнктивных форм в записи ФАЛ должно присутствовать как можно меньше элементарных конъюнкций, в которых в свою очередь должно быть как можно меньше сомножителей.
Для дизъюнктивных форм в записи ФАЛ должно присутствовать как можно меньше элементарных конъюнкций, в которых в свою очередь должно быть как можно меньше сомножителей. Y =Х2Х1X0 + Х2Х1X0 + Х2Х1X0 + Х2Х1X0 + Х2Х1X0 (2.1)
Y =Х2Х1X0 + Х2Х1X0 + Х2Х1X0 + Х2Х1X0 + Х2Х1X0 (2.1)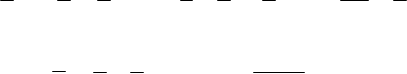 Y= X2 X1 +X2 X0 + Х2X0 = Х2(Х1 + X0) + Х2X0 = Х2Х1X0 + Х2X0 (2.5)
Y= X2 X1 +X2 X0 + Х2X0 = Х2(Х1 + X0) + Х2X0 = Х2Х1X0 + Х2X0 (2.5) 3. Метод Петрика (развитие метода Квайна-Мак Класки).
3. Метод Петрика (развитие метода Квайна-Мак Класки). У = х2х1х0 + х2х1х0 + х2х1х0 + х2х1х0 + х2х1х0 + х2х1х0 + х2х1х0 + х2х1х0 +
У = х2х1х0 + х2х1х0 + х2х1х0 + х2х1х0 + х2х1х0 + х2х1х0 + х2х1х0 + х2х1х0 + у = х2х0 + х2х1 + х1х0,+ х2х0 (2.8)
у = х2х0 + х2х1 + х1х0,+ х2х0 (2.8) При первом развертывают одну импликанту до конституент единицы, а затем смотрят, не поглощаются ли эти конституенты остальными импликантами. Первая импликанта развертывается до суммы х2х0 = х1&1&х0 = х2(х1+х1)х0= x2x1x0 + x2x1x0, причем конституента x2x1x0 не поглощается ни одной импликантой, следовательно, импликанта x2x0 не является лишней. Вторая импликанта x2x1, развертывается до суммы x2x1x0 + x2x1x0 , причем обе конституенты поглощаются остальными импликантами, следовательно, импликанта x2x1 — лишняя. Продолжим эту процедуру, оставив пока импликанту x2x1 в выражении (8). Импликанта x1x0 развертывается до суммы x2x1x0 + x2x1x0, причем обе конституенты поглощаются остальными импликантами, следовательно, импликанта x1x0 — лишняя. Продолжим, оставив в выражении (2.8) и эту импликанту. Развертывание последней импликанты дает сумму x2x1x0 + x2x1x0, в которой конституента x2x1x0 , не поглощается ни одной импликантой, следовательно, импликанта x2x0 ,не является лишней. Выявлены две лишние импликанты, но это не значит, что обе они могут быть отброшены, так как каждая из них проверялась при вхождении второй в выражение (2.8). Следовательно, отбросить наверняка можно одну из них, а затем снова произвести проверку возможности отбросить и другую. Если отбросить импликанту x2x1, то проверка показывает, что импликанта x1x0 не будет лишней, а если отбросить x1x0 , то x2x1, не будет лишней. Итак, можно отбросить одну из выявленных двух импликант. В результате получаются две ТДНФ одинаковой сложности, содержащих по 6 букв:
При первом развертывают одну импликанту до конституент единицы, а затем смотрят, не поглощаются ли эти конституенты остальными импликантами. Первая импликанта развертывается до суммы х2х0 = х1&1&х0 = х2(х1+х1)х0= x2x1x0 + x2x1x0, причем конституента x2x1x0 не поглощается ни одной импликантой, следовательно, импликанта x2x0 не является лишней. Вторая импликанта x2x1, развертывается до суммы x2x1x0 + x2x1x0 , причем обе конституенты поглощаются остальными импликантами, следовательно, импликанта x2x1 — лишняя. Продолжим эту процедуру, оставив пока импликанту x2x1 в выражении (8). Импликанта x1x0 развертывается до суммы x2x1x0 + x2x1x0, причем обе конституенты поглощаются остальными импликантами, следовательно, импликанта x1x0 — лишняя. Продолжим, оставив в выражении (2.8) и эту импликанту. Развертывание последней импликанты дает сумму x2x1x0 + x2x1x0, в которой конституента x2x1x0 , не поглощается ни одной импликантой, следовательно, импликанта x2x0 ,не является лишней. Выявлены две лишние импликанты, но это не значит, что обе они могут быть отброшены, так как каждая из них проверялась при вхождении второй в выражение (2.8). Следовательно, отбросить наверняка можно одну из них, а затем снова произвести проверку возможности отбросить и другую. Если отбросить импликанту x2x1, то проверка показывает, что импликанта x1x0 не будет лишней, а если отбросить x1x0 , то x2x1, не будет лишней. Итак, можно отбросить одну из выявленных двух импликант. В результате получаются две ТДНФ одинаковой сложности, содержащих по 6 букв: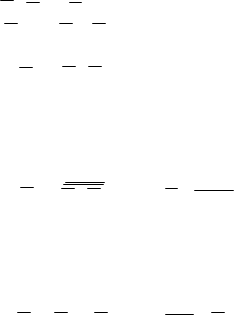 Y=х2х0+х1х0+х2х0 (2.9)
Y=х2х0+х1х0+х2х0 (2.9)

 Y
Y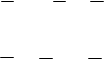 Y= x2x1 + x2x0 + x2x0 (2.14)
Y= x2x1 + x2x0 + x2x0 (2.14)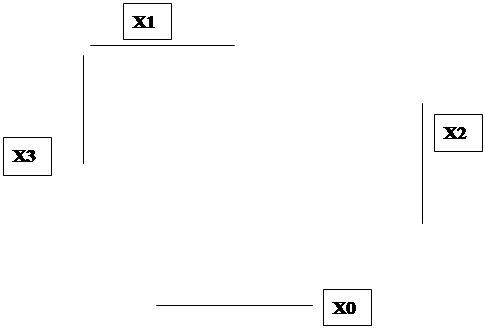

 42
42



