
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Запись логической функции с помощью базовых операцийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Каждому набору переменных соответствует один терм и только один вида Например, комбинация переменных 011 дает терм Если записать сумму всех термов, соответствующих комбинациям, на которых функция равна 1, то получим функцию, удовлетворяющую таблице соответствия (таблице истинности), т. е. определим эту функцию. Данный метод записи функции в форме суммы произведений называется “ канонической суммой ”. Можно было бы найти такой же терм в форме Пример. Проиллюстрируем эти методы записи логической функции на примере получения логической формулы функции, представленной нижеследующей таблицей:
В соответствии с первым методом рассматриваем только строки таблицы, в которых функция равна 1. Это будут вторая и третья строки функции
Согласно второму методу, рассматриваем строки, в которых функция равна нулю. Это будут первая и последняя строки функции
При записи функции выбирают тот метод, для которого меньше соответствующих символов (единиц или нулей). После представления логической функции в форме канонической суммы или в форме канонического произведения приступают к ее упрощению – минимизации. Минимизация логических функций Для упрощения булевых функций используют тождества математической логики, рассмотренные в предыдущем параграфе. На самом деле их эффективное использование требует навыков и искусства в манипулировании ими, которые приходят только после определенного опыта подобных преобразований. В то же время существует несколько стандартных приемов, которые в большинстве случаев позволяют упростить достаточно сложные логические формулы. Упрощение логического выражения начинают обычно с поиска следующих форм:
Возьмем, например, формулу:
и попытаемся ее упростить, используя изученные тождества. Группируя первый и четвертый термы, затем третий и пятый, и применяя первое из тождеств (4.2), получим:
Далее выражение упрощается без особой сложности:
Имеются также и другие методы упрощения логических функций, одним из которых является метод, использующий специальные таблицы, называемые карты Карно или диаграммы Вейча. Диаграммы Карно Данный метод состоит в том, чтобы занести логическое выражение, подлежащее упрощению, в сетку двух, трех, четырех, пяти и, возможно, шести переменных. Когда логическое выражение занесено в диаграмму Карно, оно упрощается графическими методами. Диаграммой Карно называется сетка (решетка) содержащая некоторое число пустых клеток, количество которых равно числу комбинаций переменных логической функции, подлежащей упрощению. Диаграмма двух переменных A и B будет содержать четыре клетки:
Диаграмма трех переменных A, B и C будет содержать восемь клеток:
Диаграмма четырех переменных A, B, C и D будет содержать уже шестнадцать клеток, поскольку число клеток определяется как степень двойки от числа переменных:
В случае размещения двух переменных по одной стороне диаграммы, порядок следования их комбинаций должен быть таким, чтобы при переходе от одной клетки к другой соседней клетке только одна переменная меняла свое значение, а именно: 00, 01, 11, 10. Этот порядок всегда должен соблюдаться для избежания серьезных ошибок. Для того, чтобы занести логическую функцию в диаграмму Карно, необходимо поместить единицы в клетки, соответствующие комбинациям переменных, на которых функция равна единице. Пусть, например, необходимо занести в диаграмму Карно функцию четырех переменных:
Первый терм После занесения булевой функции в диаграмму Карно, приступают к ее чтению. При этом функция будет упрощаться, если сгруппировать единицы, находящиеся в соседних клетках. Под соседними клетками понимают две клетки диаграммы Карно, для которых имеется различие в значении только одной единственной переменной. Каждый раз, когда имеются хотя бы две соседние клетки, содержащие единицы, функция, представленная в диаграмме Карно, может быть упрощена. При чтении функции единицы соседних клеток заключаются в замкнутый контур, что означает, что эти единицы сгруппированы вместе для получения упрощенного выражения функции. В одной и той же диаграмме может существовать множество соседних единиц. В этом случае организуют множество контуров и записывают сумму полученных упрощенных термов. Имеется возможность получения наиболее простого решения, т. е. содержащего минимум логических переменных для рассматриваемой функции, заключая в контур максимум соседних клеток. Для этого контуры делают максимально возможно большими. Пусть, например, необходимо записать аналитическое выражение логической функции, представленной в заданной диаграмме:
Заключая единицы в соседних клетках в три контура, получают следующее логическое выражение:
Использование диаграмм Карно представляет собою элегантный и эффективный метод упрощения логических схем. Он состоит в следующем: на основании определенной логической схемы записывается логическое выражение выхода, выраженное в функциях входных переменных, затем выражение, занесенное в диаграмму Карно, упрощается методом контуров, рассмотренным выше, и на основании полученного выражения создается новая схема. Пусть, например, необходимо упростить логическую схему, представленную на рис. 4.1. В соответствии с этой схемой логическое выражение, описывающее ее выход, будет иметь следующий вид:
Занесем значение функции
После упрощения мы получим следующее значение функции:
и для функции
Откуда получим схему, представленную на рис. 4.2., эквивалентную схеме рисунка 4.1.
Контрольные задания Произвести минимизацию одной из заданных логических функций двумя способами – используя законы и тождества Булевой алгебры и с помощью диаграмм Карно. 4.1. 4.2. 4.3. 4.4. 4.5. 4.6. 4.7. 4.8. 4.9. 4.10.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 685; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.67.189 (0.008 с.) |

 такой, что он будет равен 1 для рассматриваемой комбинации и 0 для всех остальных комбинаций.
такой, что он будет равен 1 для рассматриваемой комбинации и 0 для всех остальных комбинаций.
 , равный 0 для одной единственной комбинации и 1 для всех остальных комбинаций. Тогда функция будет записана в форме произведения подобных термов, и будет называться “ каноническим произведением ”.
, равный 0 для одной единственной комбинации и 1 для всех остальных комбинаций. Тогда функция будет записана в форме произведения подобных термов, и будет называться “ каноническим произведением ”.
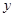

 и
и  . Беря их логическую сумму, получим
. Беря их логическую сумму, получим
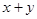 и
и  . Беря их логическое произведение, получим
. Беря их логическое произведение, получим
 ,
,  ,
,  , где
, где  и
и  обозначают либо сами логические переменные, либо логические произведения множества переменных. Каждое из полученных выражений может быть записано в более простой форме следующим образом:
обозначают либо сами логические переменные, либо логические произведения множества переменных. Каждое из полученных выражений может быть записано в более простой форме следующим образом:
 (4.2)
(4.2)




 дает единицу в клетке, для которой A = 0, B = 1, C = 0 и D = 1, т. е. в клетке, находящейся на пересечении второй строки и второго столбца. Второй терм
дает единицу в клетке, для которой A = 0, B = 1, C = 0 и D = 1, т. е. в клетке, находящейся на пересечении второй строки и второго столбца. Второй терм  дает две единицы в клетках, для которых A = 1, B = 1, C = 0, а значение D безразлично, т. е. может быть равно как нулю, так и единице. Данные комбинации соответствуют клеткам, находящимся на пересечении третьего столбца и первой и второй строк. Третий терм
дает две единицы в клетках, для которых A = 1, B = 1, C = 0, а значение D безразлично, т. е. может быть равно как нулю, так и единице. Данные комбинации соответствуют клеткам, находящимся на пересечении третьего столбца и первой и второй строк. Третий терм  даст четыре единицы в клетках, для которых A = 0, D = 1, а значения B и C могут быть равны как нулю, так и единице, что соответствует клеткам, находящимся на пересечении первого и второго столбцов и второй и третьей строк. На остальных комбинациях функция равна нулю, поэтому в оставшиеся клетки вносится значение 0.
даст четыре единицы в клетках, для которых A = 0, D = 1, а значения B и C могут быть равны как нулю, так и единице, что соответствует клеткам, находящимся на пересечении первого и второго столбцов и второй и третьей строк. На остальных комбинациях функция равна нулю, поэтому в оставшиеся клетки вносится значение 0. III
III
 1
1
 1
1
 1
1


 и
и 
 в соответствующую диаграмму Карно:
в соответствующую диаграмму Карно: AB
AB
 0
0
 0
0
 1
1

 , заключая в контуры нули диаграммы, получим:
, заключая в контуры нули диаграммы, получим:
 Можно заметить, что схема рисунка 4.2. значительно экономичнее схемы рисунка 4.1.
Можно заметить, что схема рисунка 4.2. значительно экономичнее схемы рисунка 4.1.












