
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение логической функцииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Логическая функция от n переменных x1, x2, …, xn – это функция, которая может принимать только два значения 0 или 1. Каждая переменная может принимать только два значения. Следовательно имеется 2n возможных комбинаций n переменных. Логическая функция будет определена, если известно ее значение для каждой из 2n возможных комбинаций. Она может быть представлена с помощью соответствующей таблицы истинности. Рассмотрим, например функцию трех переменных f(x,y,z). Функция f(x,y,z) будет определена, если будут заданы ее значения (0 или 1) для каждой из восьми комбинаций таблицы:
Следует отметить, что имеется 2N способов присвоить значения 0 или 1 функции для N комбинаций переменных. Поскольку N=2n, то, следовательно, существует Логические функции одной переменной Существует
Функции f0 и f3 – это константные функции, равные нулю и единице независимо от значения аргумента x и называются они: конституанта нуля и конституанта единица соответственно. Функция f1 совпадает с аргументом x: f1(x) = x. Функция f2 противоположна значению аргумента: f2(x) = Логические функции двух переменных Имеется Функции f0 и f15 – конституанты 0 и 1 соответственно. Функция f3 не зависит от y и равна x (f3(x,y) = x). Функция f5 не зависит от x и равна y (f5(x,y) = y). Функция f10 не зависит от x и является отрицанием переменной y (f10(x,y) = Функция f12 не зависит от y и является отрицанием переменной x (f12(x,y) = Оставшиеся функции являются функциями, непосредственно зависящими от двух переменных x и y. Среди них можно выделить наиболее часто употребляемые функции f1 и f7.
Функция f1 принимает истинное значение (значение 1), если и только если оба аргумента одновременно являются истинными (x=1 и y=1). Ее называют “конъюнкция”, или же “ функция логического умножения ”, или же “ функция И ” и обозначают обычно как f(x,y) = xy.
Функция f7 принимает значение 1, если хотя бы один из аргументов x = 1 или y = 1. Ее называют “ дизъюнкция”, или же “функция логического сложения”, или же “ функция ИЛИ ” и обозначают обычно как f7(x,y) = x + y. Функция f6(x,y) = Функция f9(x,y) = Функция f8(x,y) = Функция f14(x,y) = Функция f2(x,y) = Функция f4(x,y) = Функция f11(x,y) = Функция f13(x,y) = Основные операции Булевой алгебры На практике определяют некоторое число основных операций, с помощью которых можно описать все остальные операции. Такие операции называются функционально полным набором. Среди всех наборов обычно выделяют один, состоящий из трех операций: логическая инверсия, логическое сложение и логическое умножение.
Операция инверсии Результат операции инверсии обозначают, добавляя черту над переменной x. f(x) =
На структурных схемах данную логическую функцию обозначают с помощью следующего символа: Логическое сложение Операция логического сложения, соответствующая функции ИЛИ, выдает в качестве результата значение, называемое логической суммой. В выражениях для этой операции приняты следующие обозначения:
На схемах эта функция обозначается с помощью символов: Логическое умножение Логическое умножение соответствует функции И, и выдает в качестве результата значение, называемое логическим произведением. В выражениях для этой операции приняты следующие обозначения:
На схемах эта функция обозначается с помощью символов:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 1937; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.167.32 (0.01 с.) |

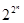 различных функций n переменных.
различных функций n переменных.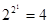 логических функций одной переменной. Обозначим эти 4 функции как f0 - f3. Значение индекса функции равно значению ее двоичного представления в соответствующей колонке таблицы истинности:
логических функций одной переменной. Обозначим эти 4 функции как f0 - f3. Значение индекса функции равно значению ее двоичного представления в соответствующей колонке таблицы истинности: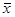 . Эту функцию называют “ инверсия ”, “отрицание” или же функция НЕ.
. Эту функцию называют “ инверсия ”, “отрицание” или же функция НЕ.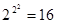 логических функций двух переменных. Определения этих функций, обозначенных от f0 до f15, даны в нижеследующей таблице.
логических функций двух переменных. Определения этих функций, обозначенных от f0 до f15, даны в нижеследующей таблице.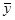 ).
).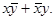 Это функция “ исключающее ИЛИ ” (f6(x,y) = 1, если x = 1 или y = 1, но не одновременно). Еще ее называют “ сумма по модулю 2 ”, или же “ функция несовпадения ”. Операция, которая соответствует этой функции, часто обозначается в виде
Это функция “ исключающее ИЛИ ” (f6(x,y) = 1, если x = 1 или y = 1, но не одновременно). Еще ее называют “ сумма по модулю 2 ”, или же “ функция несовпадения ”. Операция, которая соответствует этой функции, часто обозначается в виде 
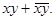 Это функция “ логической идентичности ” или же “ функция совпадения ”. (f9(x,y) = 1, если x и y имеют одинаковые значения). Ее иногда обозначают как
Это функция “ логической идентичности ” или же “ функция совпадения ”. (f9(x,y) = 1, если x и y имеют одинаковые значения). Ее иногда обозначают как 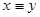 или
или  ~
~ 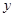 .
.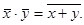 Это “ функция НИ ” (f8(x,y) = 1, если ни x ни y не равны 1), или же функция “ стрелка Пирса ”, обозначаемая иногда как
Это “ функция НИ ” (f8(x,y) = 1, если ни x ни y не равны 1), или же функция “ стрелка Пирса ”, обозначаемая иногда как 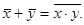 Это функция “ логической несовместимости ” (f14(x,y) = 1, если x и y одновременно не равны 1), или же функция “ штрих Шеффера ”, обозначаемая иногда как
Это функция “ логической несовместимости ” (f14(x,y) = 1, если x и y одновременно не равны 1), или же функция “ штрих Шеффера ”, обозначаемая иногда как 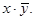 Она называется “ функция запрещения ” (f2(x,y) = 1, если x = 1 и y = 0), иногда обозначаемая как
Она называется “ функция запрещения ” (f2(x,y) = 1, если x = 1 и y = 0), иногда обозначаемая как 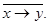
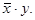 Она называется “ функция запрещения ” (f4(x,y) = 1, если x = 0 и y = 1), иногда обозначаемая как
Она называется “ функция запрещения ” (f4(x,y) = 1, если x = 0 и y = 1), иногда обозначаемая как 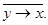
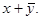 Это функция “ вовлечения ” или “ следования ” (f11(x,y) = 1 для всех комбинаций аргументов, кроме x = 0 и y = 1), обозначаемая иногда как
Это функция “ вовлечения ” или “ следования ” (f11(x,y) = 1 для всех комбинаций аргументов, кроме x = 0 и y = 1), обозначаемая иногда как  или
или 
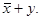 Это функция “ вовлечения ” или “ следования ” (f13(x,y) = 1 для всех комбинаций аргументов, кроме x = 1 и y = 0), обозначаемая иногда как
Это функция “ вовлечения ” или “ следования ” (f13(x,y) = 1 для всех комбинаций аргументов, кроме x = 1 и y = 0), обозначаемая иногда как 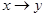 или
или 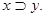

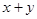 или
или 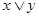 . Таблица определения или таблица истинности этой операции имеет вид:
. Таблица определения или таблица истинности этой операции имеет вид: или
или 
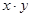 , или
, или 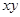 , или же
, или же 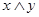 . Таблица определения или таблица истинности этой операции имеет вид:
. Таблица определения или таблица истинности этой операции имеет вид: или
или 



