
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Минимизация нормальных форм булевых функций.Содержание книги
Поиск на нашем сайте Билет 1 Билет 18 Способы задания множеств. Подмножество данного множества. Характеристические функции. Равенство множеств. Одноэлементное множество. Неупорядоченная пара. Множество всех подмножеств данного множества. Операции над множествами. Под множеством А мы понимаем собрание определённых и различных между собой объектов мыслимых как единое целое. Эти объекты называются элементами множества. а а Характеристическая функция:
Виды множеств: -Множества, состоящие из конечного числа элементов, называются конечными. (Число элементов конечного множества называется его мощностью) -Пустое множество: множество мощностью 0, т.е не содержащее ни одного элемента, называется пустым. -Универсальное множество: это любое изучаемое в данный момент множество. Способы задания множеств. 1. Перечислением (списком своих элементов) А = 2. Описанием характеристических свойств.(которыми должны обладать его элементы)
x 3. Порождающие процедурой. (которая описывает способ получения элементов множества из уже полученных либо из других объектов) Рассмотрим след. пример X Q 1.3 2.x 3.Для других элементов, кроме тех которые построены по пунктам 1,2 в Х нет Х= Замечание:Задание множеств с помощью описаний может приводить к противоречиям. Операции над множествами. Пусть А и В произвольные множества, заданные на 1)пересечение: А 2)объединение: A 3)относительное дополнение: A\B= {x 4)симметрическая разность: A+B= (A\B) 5)абсолютное дополнение:
Равенство множеств: Условимся говорить, что множества А и В равны и писать А=В, если А и В состоят из одних и тех же элементов.
Множество A, содержащее один элемент a, обозначается A = {a} и называется одноэлементным. Неупорядоченная пара – множество из 2х элементов без указания их очерёдности. Множество всех подмножеств множества A называется булеаном A (также степенью множества, показательным множеством или множеством частей) и обозначается 2^А Число подмножеств конечного множества, состоящего из n элементов, равно 2n(док-во по индукции разделяя мно-во М на 2 множ-ва М1(содержит а) и М2=М-{a0} -1 A -2 A -3 A -4 А -5 А -6 А -7 А -8 A -9 А -10 A -11 -12 -13 -14 А = (A -15 А = (А -16 A -17 A -18 A -19 A -20 A -21 A -22 А\В = А
Билет 1 Билет 2 Булевы функции, суперпозиция, существенные и фиктивные переменные. Нормальные формы Л – 0 И – 1 { 0,1} = В Функция f(х1, х2 … хn)определенная на множестве Вn и принимающая значения из множества В, называется булевой функцией n – переменных. В математике компози́ция фу́нкций (суперпози́ция фу́нкций) — это применение одной функции к результату другой. Существенная –если в каком-либо наборе от её значения зависит значение функции(иначе фиктивная) ДНФ и КНФ Элементарная & и V. Элементарная &(V) называется &(V) формул, каждая из которых есть либо высказывательная переменная, либо отрицание высказывательной переменной. Конъюнктивной нормальной формой (КНФ) данной формы называется равносильная ей форма, состоящая из конъюнкций (&) элементарных дизъюнкций (V). ДНФ данной формулы называется равносильная ей формула, состоящая из V элементарных &. Билет 3 Натуральные числа в теории множеств. Аксомы Пеано. (Через пустые множества) Аксиомы 1 является натуральным числом; Число, следующее за натуральным, также является натуральным; 1 не следует ни за каким натуральным числом; Если натуральное число а непосредственно следует как за числом b, так и за числом c, то b и c тождественны; (Аксиома индукции) Если какое-либо предложение доказано для 1 (база индукции) и если из допущения, что оно верно для натурального числа, вытекает, что оно верно для следующего за натурального числа (индукционное предположение), то это предложение верно для всех натуральных чисел.
Билет 3 Билет 4 Билет 4 Нахождение кратчайшего пути АЛГОРИТМ ФРОНТА ВОЛНЫ ПОИСКА МИНИМАЛЬНОГО ПУТИ ИЗ ВЕРШИНЫ a в b в орграфе G: (12 номер из курсовой) 10 Помечаем вершину а индексом 0, а все вершины, принадлежащие образу вершины а Г(а) индексом 1. Множество вершин, помеченных индексом 0, 1 обозначаем FW0(a) FW1(A) Полагаем k:=1 20 Если FWk(a)=∅ или при k=n-1 b∉FWn-1(a), то вершина b недостижима из a и алгоритм заканчивает свою работу(выход). В противном случае (FWk(a)≠∅) переходим к шагу 30 30 Если?b∈FWk(a)?, то переходим к шагу 40, в противном случае (?) существует путь из а в b длины k и этот путь минимален. Он задается последовательностью вершин. a=x0 x1 x2.... xk-2 xk-1 xk=b, где xk-1∈FWk-1(a)∧Г-1(b); xk-2∈FWk-2(a)∧Г-1(xk-1);....; x1∈FW1(a)∧Г-1(x2); на этом алгоритм заканчивает свою работу(выход) 40 Помечаем индексом k+1 все непомеченные вершины, которые принадлежат образу множества вершин помеченных индексом k. Множество вершин с индексом k+1 обозначаем Wk+1(a). Полагаем k:=k+1 и переходим в шагу два. Замечание1: FWk(a) - фронт волны k-ого уровня. Замечание2: Вершины х1х2...хk-2,xk-1 вообще говорят могут быть выделенны неоднозначно, т.е. может существовать несколько минимальных путей. Замечание3: FWk+1(a) отыскивается по рекурентной форме: FWk+1=Г(FWk(a))\ ∨i=0KFWi(a). Алгоритм Флойда-Оршалла Алгоритм Дейкстры Алгоритм Форда Помечаем вершину xi индексом λi; Полагаем a=x6 и присваиваем ей λ6, причем λ0=0, а все остальные вершины помечаем λj=∞. Помечаем <xi,xj> для которой λi- λj˃l(xi,xj), затем заменяем индекс λj на индекс λ/J; λ/J= λi+ l(xi,xj)< λj Продолжаем процесс до тех пор пока не перестанут уменьшаться индексы. Предположим что алгоритм Форда выполним, тогда λn= λρ0. Среди дуг будет та по которой алгоритм Форда применим: λn- λρ1= l(x ρ1, xn) λ ρ1- λρ2= l(x ρ1, x ρ1) ………………… λ ρk- λ0= l(x 0, x ρk) ________________ (сложим все эти равенства) λ n= l(x 0, x ρk…………. x n). Возьмем x 0, x k1…………. x n предположим что он короче чем тот который мы нашли по алгоритму Форда: Λ0, λк1……………………………………………. λкn, -индексы присвоены по алгоритму Форда, где выполняется: Λk1- λ0≤ l(x 0, xr1) λ k2- λk1≤ l(x k1, x k2) ………………… λ n- λks≤ l(x ks, x n) ________________ (сложим все эти равенства) λ n≤l(x 0, x k…………. x n). значит метод Форда минимальный путь. Алгоритм Форда-Беллмана. Замечание: он позволяет по таблице значений λ(к)i (i=1…..n), (k=0,1……..n-1) и матрицы длин дуг λ(к)i= Замечание: к=0,1…………….n-1, λ1(к)=0; λ(0)i=∞, i=2,3…….n. Матрицу весов С опишем следующим образом Cij=
Билет 5 Билет 5 Билет 20 Билет 6 Билет 19 Билет 6 Билет 7 Билет 7 Билет 19 Билет 8 Билет 8 Билет 18 Билет 9 Билет 9 Билет 10 Билет 10 Билет 11 Плоские и планарные графы. Теорема Эйлера. Планарный граф — граф, который может быть изображен на плоскости без пересечения ребер.
Более строго: Граф укладывается на некоторой поверхности, если его можно на ней нарисовать без пересечения ребер. Уложенный граф называется геометрическим, его вершины — это точки плоскости, а ребра — линии на ней. Области, на которые граф разбивает поверхность, называются гранями. Плоский граф — граф, уложенный на плоскость. Граф называется планарным, если он изоморфен некоторому плоскому графу.
Непланарны К5(полный) и К33
Теорема Эйлера Вершины – рёбра + грани = 2 Докво по индукции (добавл 1 грань, r ребер и r-1 вершину)
Билет 12 Билет 12 Билет 13 Билет 13 Билет 14 Билет 14 Билет 15 Решетки. Группы. Кольца. Решётка, структура — частично упорядоченное множество, в котором каждое двухэлементное подмножество имеет как точную верхнюю (sup), так и точную нижнюю (inf) грани. Отсюда вытекает существование этих граней для любых непустхконечных подмножеств.
Билет 15 Билет 16 Булевы решётки Булева алгебра, булева решётка — частично упорядоченное множество специального вида; дистрибутивная решётка, имеющая наибольший элемент 1 — единицу булевой алгебры, наименьший элемент 0 — нуль булевой алгебры, и содержащая единственное дополнение каждого своего элемента x — элемент (не x)
Билет 16 Билет 17 Булево кольцо Булевым кольцом называют кольцо, в котором все элементы идемпотентны (коммутативность, наличие единицы или делителей нуля не требуется). Интересной особенностью булевых колец является то, что
в частности, при
то есть булево кольцо всегда коммутативно.
Билет 17 Билет 20 Билет 1 Билет 18 Способы задания множеств. Подмножество данного множества. Характеристические функции. Равенство множеств. Одноэлементное множество. Неупорядоченная пара. Множество всех подмножеств данного множества. Операции над множествами. Под множеством А мы понимаем собрание определённых и различных между собой объектов мыслимых как единое целое. Эти объекты называются элементами множества. а а Характеристическая функция:
Виды множеств: -Множества, состоящие из конечного числа элементов, называются конечными. (Число элементов конечного множества называется его мощностью) -Пустое множество: множество мощностью 0, т.е не содержащее ни одного элемента, называется пустым. -Универсальное множество: это любое изучаемое в данный момент множество. Способы задания множеств. 1. Перечислением (списком своих элементов) А = 2. Описанием характеристических свойств.(которыми должны обладать его элементы)
x 3. Порождающие процедурой. (которая описывает способ получения элементов множества из уже полученных либо из других объектов) Рассмотрим след. пример X Q 1.3 2.x 3.Для других элементов, кроме тех которые построены по пунктам 1,2 в Х нет Х= Замечание:Задание множеств с помощью описаний может приводить к противоречиям. Операции над множествами. Пусть А и В произвольные множества, заданные на 1)пересечение: А 2)объединение: A 3)относительное дополнение: A\B= {x 4)симметрическая разность: A+B= (A\B) 5)абсолютное дополнение:
Равенство множеств: Условимся говорить, что множества А и В равны и писать А=В, если А и В состоят из одних и тех же элементов.
Множество A, содержащее один элемент a, обозначается A = {a} и называется одноэлементным. Неупорядоченная пара – множество из 2х элементов без указания их очерёдности. Множество всех подмножеств множества A называется булеаном A (также степенью множества, показательным множеством или множеством частей) и обозначается 2^А Число подмножеств конечного множества, состоящего из n элементов, равно 2n(док-во по индукции разделяя мно-во М на 2 множ-ва М1(содержит а) и М2=М-{a0} -1 A -2 A -3 A -4 А -5 А -6 А -7 А -8 A -9 А -10 A -11 -12 -13 -14 А = (A -15 А = (А -16 A -17 A -18 A -19 A -20 A -21 A -22 А\В = А
Билет 1 Минимизация нормальных форм булевых функций. Анализ требований к задаче минимизации ДНФ обнаружил ря общих свойств и позволил ввести особую меру сложности ДНФ. Пусть F=F1∨F2∨...∨Fm, т.е. заданна в виде ДНФ булевой функции. О: отображение L составляющая каждой ДНФ целое неотрицательное число и удовлетворяющая требованиям 1) 2) 3) 4) называется индексом простоты 1) L(F)≥0 2) F=F1∨(xi&F2) => L(F)≥L(F1∨F2) 3) Если F=F1∨F2 => L(F)≥L(F1)+L(F2) 4) Если ДНФ F1 получена из ДНФ F2 переименованием переменных, то L(F1)=L(F2) В качестве индекса простоты можно взять: Lk(F)- число элементарных конъюнкций, входящих в F Lr(F)- сумма рангов элементарных конъюнкций, входящих в F. Рангом называется число переменных r входящих в Fi элементарную конъюнкцию ДНФ F. L0(F)-число отрицаний в F. О: Минимальная ДНФ - ДНФ F, реализующая заданную булеву функцию и имеющая минимальное значение L(F) называется минильной (относительно индекса простоты L). Замечание: ДНФ минимальная относительно индекса Lr -просто минимальной, Lk- кратчайшей. Сокращенные и тупиковые ДНФ {не уверен что ето надо, но напечатал на всякий случай} О: Говорят, что функция F1 своим значением с1 накрывает значение с2 функции F2, если на некоторой оценке <ε1,ε2,...εn> списка переменных <x1,x2,...,xn> то F1(ε1...εn)=c1 F2(ε1...εn)=c2 О: Функция F1 называется импликантой функции F2, если она своими нулями накрывает все нули функции F2 Т1: Если F1,F2,...,Fm импликанты булевой функции F, то F1∨F2∨...∨Fm F1&F2&...&Fm, также импликанты. Т2: Если F1∨F2∨...∨Fm импликанты булевой функции, то и F1,F2,...,Fm тоже импликанты. О: простая импликанта - элементарная конъюнкция, входящая в ДНФ булевой функции F называется её простой импликантой, если никакая её часть не является импликантой булевой функции F. Т3: Дизъюнкция всех простых импликант булевой функции совпадает с этой булевой функцией. О: СкДНФ - ДНФ, составленная ищ простых импликант булевой функции называется сокращенной ДНФ(СкДНФ) Простые импликанты называются лишними, если они могут быть удалены из ДНФ и при этом значение функции не изменится ни в одной. О: Тупиковая ДНФ - сокращенная ДНФ из которой удалены лишние импликанты называются тупиковой (ТДНФ) Метод минизации Квайна: Здесь рассматриваются булевы функции приведенные к СДНФ(в виде F=F1∨F2∨...∨Fm, где Fi - элементарная конъюнкция, содержащая весь список переменных <x1,...,xn> Метод квайна основан на двух операциях: 1) (X&A)∨(X&A)≡(X&A)∨(X&A)∨A 2) A∨(A&B)≡A Метод Квайна основан на следующей теореме: Т.Квайна: Если в СДНФ произвести все возможные неполные склеивания, а затем все возможные поглощения, то получится СкДНФ. Алгоритм минимизации: 10 Находим СДНФ, которая реализует заданную булеву функцию. 20 Находим ей эквивалентную СкДНФ по Т.Квайна. 30 Находим множество тупиковых ДНФ, каждая из которых реализует булеву функцию 40 Из множества тупиковых ДНФ по опр. минимальности находим минимальную ДНФ.
Билет 2
|
||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 521; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.007 с.) |

 А
А А,
А, 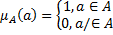

 - универсальное множество.
- универсальное множество. , Р(х) – предикаты.
, Р(х) – предикаты. 1/x, 1-x
1/x, 1-x 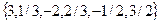
 В = {x
В = {x  B = {x
B = {x  B}
B} =
=  = А
= А
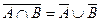
 )
)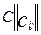 нагруженного орграфа определить минимальный путь из вершины а в любую достижимую вершину, причем из всех возможных путей он выделяет путь с наименьшим числом дуг.
нагруженного орграфа определить минимальный путь из вершины а в любую достижимую вершину, причем из всех возможных путей он выделяет путь с наименьшим числом дуг.











