
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ориентированные и неориентированные графы. Подграфы и частичные графы. Пути и контуры, цепи и циклы. Операции над графами.Содержание книги
Поиск на нашем сайте ОРИЕНТИРОВАННЫЕ ГРАФЫ.(ОРГРАФЫ) Пусть Х не пустое множество, а Х2=Х×Х - множество всех его пар. О: Пара <Г,Х>=G называется ориентированным графом (орграфом), где Г-произвольное подмножество множества Х2 (Г⊆Х2) Элементы х∈Х называются вершинами, а пара <X,Y>∈Г дугами орграфа. Замечание: тройку множеств <Г,Х,Y>, где Г⊆Х,Y называют многозначным отображателем из множества Х во множестве У. Обозначают Г:Х+Y. При этом, если х∈Х, то множество Г(х)={y∈Y|<x,y>∈Г}⊆Y называют образом элемента х, а Г-1(y)={x∈X|<x,y>∈Г}⊆X называют прообразом y. Если А⊆Х, то Г(А)=∨х∈АГ(х) - это образ множества А А⊆Y, то Г-1(А)=∨y∈AГ-1(А) - это прообраз мн-ва А Пусть задан орграф G=<Г,Х> 1. если y∈Г(х), т.е. <x,y> дуга, то говорят что она исходит из вершины х и заходит в у. 2. Дуга называется инцидентной в вершине х, если она заходит в х или исходит из х. 3. Дуга <x,х> называется петлей. 4. Вершина, не имеющая инцидентных дуг называется изолированной. Две вершины называются смежными, если существует дуга инцидентная им обоим. Пути в орграфе. О1: Последовательность дуг орграфа такая что начало каждой последующей дуги совпадает с концом предыдущей называется путем. О2: Путь у которого начало первой дуги совпадает с концом последней называется замкнутым путем, или контуром. О3: Путь (контур) называется элементарным, если все его вершины различны за исключением первой и последней. О4:Путь (контур) называется простым, если все его дуги различны. Примеры: 1) <x1,x2> <x2,x5> <x5,x4> - не контур, но простой эл-ый путь. 2) <x1,x2> <x2,x3> <x3,x1> - эл-ый простой путь, контур. 3) <x1,x2> <x2,x5> <x5,x4> <x4,x2> <x2,x3> <x3,x1> - контур, простой, не эл-ый 4) <x1,x2> <x2,x3> <x3,x1> <x1,x2> <x2,x3> <x3,x1> - не простой, не эл-ый, контур 5) <x1,x2> <x2,x5> <x5,x4> <x4,x2> <x2,x3> - не путь НЕОРИЕНТИРОВАННЫЕ ГРАФЫ Пусть Х-непустое множество. Х(2) - мн-во всех 2-х элементарных подмножеств множества Х. Пример: Х={1,2,3}. X(2)={{1,2},{1,3},{2,3}} О: Пара <Q,X>=G, где Q произвольное подмножество множества Х (Q⊆X) называется неориентированным графом. Элементы х∈Х - вершинами, а элементы {x,y}∈Q - (неупорядоченные пары) - ребрами. Замечание: неориентированные графы можно изучать как графы симметричных бинарных отношений. Подграфом графа G называется G’, если X’⊂X, Q’⊂Q (Г’⊂Г), а в случае если X’=X, то подграфом называют частичным графом. О1: Цепью неориентированного графа называется последотельность ребер, которая может быть перемещена в путь введением соответствующей ориентации на её ребрах. О2: Циклом называется цепь у которой 1-ая вершина совпадает с последней. О3: Цепь (цикл) называется элементарной, если некоторая вершина встречается в ней не более одного раза. О4: Цепь (цикл) называется простой, если некоторой ребро встречается в ней не более одного раза. Последовательность дуг орграфа такая, что начало каждой последующей дуги совпадает с концом предыдущей называется путём. Путь у которого начало первой дуги совпадает с концом последней называется замкнутым путём или контуром. Путь(контур) называется элементарным, если все его вершины различны(за искл. Первой и последней) Путь (контур) называется простым, если все его дуги различны. 1 )Цепью неор графа называется последовательность рёбер которая может быть превращена в путь введением соответственной ориентации на её ребрах. 2) Цепь у которой первая вершина совпадает с последней называется циклом. 3)Цепь(цикл) называется элементарной, если некоторая вершина встречается в ней не более одного раза. 4) Цепь (цикл) называется простой, если некоторое ребро встречается в ней не более одного раза. Вершины х, у неор графа G называются связными, если существует цепь из х в у. Неориентированный граф называется связным если все его вершины связны. Утверждение: отношение связности ρ – отношение эквивалентности. 1. Xρx - рефлексивность 2. xρy => yρx - симметричность 3. xρy и yρz => xρz – транзитивность Подграф G' графа G называется компонентой связности графа G, если все вершины G' составляют класс эквивалентности по отношению связности, а множество рёбер G' это все инцидентные этим вершинам рёбра. Замечание1: для ор. Графа можно ввести несколько понятий связности. Говорят что вершина «у» орграфа G достижима из вершины «х», если либо «х=у», либо существует путь из «х» в «у». Ор.граф называется сильно связным, если для любых двух его вершин «х» и «у» существует путь из «х» в «у». Ор.граф называется односторонне связным, если для любых двух его вершин по крайней мере одна достижима из другой.
Эйлеровы цепи. Цепь М называется эйлеровой, если она содержит все ребра графа и при том по одному разу.
Гамельтоновы цепи. Цепь М называется Г амельтоновой, если она проходит через каждую вершину графа 1 и только 1 раз. Плоские графы. Говорят что граф имеет плоскую реализацию(планарен), если он может быть изображен на плоскости без пересечения рёбер. Операция подразделения ребра. G=<Г,x> G->G’ Q’=Q\ x’=xU{a} a – новая величина Граф Замечание: обратная операция слияния двух рёбер применима лишь тогда, когда оба они обладают общей инцидентной вершиной, неинцидентной никаким другим рёбрам. Гомеоморфизм. Графы переводимые друг в друга конечным числом подразделения и слияния рёбер называется – гомеоморфными. Оношение гомеоморфизма есть отношение эквивалентности, заданное на множестве всех неор. Графов. 1)GpG - рефлексивность 2) 3) Критерий планарности.Теорема Пантрягина-Куратовского. Для того чтобы граф G имел плоскую ориентацию, необходимо и достаточно, чтобы любой его подграф не был гомеоморфен не одному из графов. Операции над графами Объединение Пересечение Кольцевая сумма (Другими словами, граф не имеет изолированных вершин и состоит только из ребер, присутствующих либо в 1, либо в 2, но не в обоих одновременно) Удаление вершины Удаление ребра(дуги) Замыкание(две вершины заменяются одной, так, что рёбра инцедентные 1 становятся инцедентны 2).(на вершине образуется кольцо и неё в неё) Стягивание(замыкание с удалением ребра, то же, что и замыкание только без кольца) Билет 4
|
||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 475; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.005 с.) |

 Граф G обладает эйлеровой цепью тогда и только тогда когда он связен и число вершин нечётной степени равно нулю или два(если таких вершин нет то существует эйлеров цикл)
Граф G обладает эйлеровой цепью тогда и только тогда когда он связен и число вершин нечётной степени равно нулю или два(если таких вершин нет то существует эйлеров цикл)
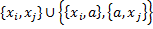
 называется подразделением графа
называется подразделением графа  , если он может быть получен из
, если он может быть получен из  р
р  =>
=> 


