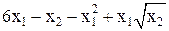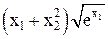Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лабораторная работа № 9. Многомерный поиск. Методы безусловной минимизацииСодержание книги
Поиск на нашем сайте
Задание: Найти положение точки экстремума и экстремальное значение целевой функции
Вопросы для самоподготовки
1. В чем состоит общая задача нелинейного программирования? 2. На какие группы делятся методы решения задач безусловной минимизации? 3. Дайте краткую характеристику методов безусловной минимизации: итерационный характер методов; проблема выбора шага; выбор направления поиска. 4. Опишите алгоритм метода покоординатного спуска. 5. Как выбирается направление спуска в методе покоординатного спуска? 6. При выполнении какого условия следует прекратить поиск? 7. Составьте блок-схему метода покоординатного спуска. 8. Дайте сравнительную характеристику градиентных методов оптимизации. 9. Дайте описание алгоритма метода наискорейшего спуска. 10. Как решается проблема выбора шага и направления в методе наискорейшего спуска? 11. Дайте описание алгоритма метода сопряженных направлений. 12. В чем состоит основное отличие методов наискорейшего спуска и сопряженных направлений? 13. Какие методы условной минимизации вы знаете? 14. В чем главное отличие методов условной минимизации от методов безусловной минимизации? 15. Метод сканирования. 16. Каково минимальное количество вычислений целевой функции для метода сканирования? 17. Укажите область использования метода сканирования. 18. Метод штрафных функций. 19. На какие классы можно разделить методы штрафных функций? 20. Чем характеризуются параметрические методы?
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 305; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.219.252 (0.01 с.) |

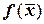 методом наискорейшего спуска (подъема) с точностью 0,001, если заданы координаты исходной точки
методом наискорейшего спуска (подъема) с точностью 0,001, если заданы координаты исходной точки  .
.