
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лабораторная работа № 6. Численное решение обыкновенных дифференциальных уравненийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Задание: Найти численное решение задачи Коши для данного дифференциального уравнения и начального условия
Вопросы для самоподготовки 1. Общая постановка задачи Коши. 2. Что является решением задачи Коши? Каков его геометрический смысл? 3. В чём состоит численное решение задачи Коши? 4. Метод Эйлера (алгоритм, геометрическая интерпретация, программа). 5. Метод Рунге-Кутта второго порядка (алгоритм, геометрическая интерпретация, программа). 6. Метод Эйлера-Коши (алгоритм, геометрическая интерпретация, программа).
Лабораторная работа № 7. Численное решение дифференциальных уравнений в частных производных
Задание: Методом сеток решить уравнение теплопроводности - диффузии Решение выполнить при шаге по длине - h=0.1, а шаг по времени - t, выбрать самостоятельно. Построить график изменения температуры по длине для каждого шага по времени.
Вопросы для самоподготовки
1. Классификация дифференциальных уравнений в частных производных. 2. Начальные условия. Типы граничных условий. 3. Конечно-разностные аппроксимации производных первого и второго порядка. 4. Построение разностных схем для уравнений с частными производными. Шаблоны. 5. Явная разностная схема для решения одномерного уравнения диффузии – теплопроводности. Понятие устойчивости вычислительной схемы. 6. Неявная разностная схема для решения одномерного уравнения диффузии – теплопроводности.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 508; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.011 с.) |

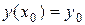 на отрезке
на отрезке 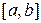 с шагом
с шагом  . Использовать метод, указанный преподавателем.
. Использовать метод, указанный преподавателем.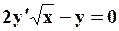
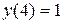
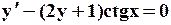
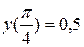
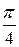

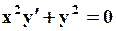
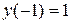
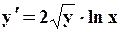
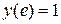

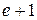
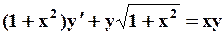
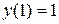

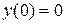
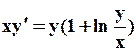

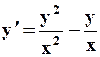

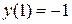

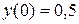

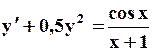
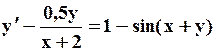
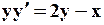
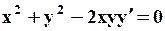


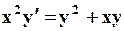
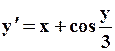
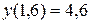
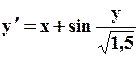
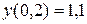

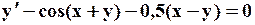
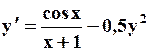


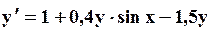

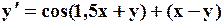
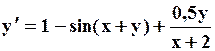
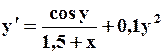



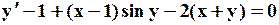

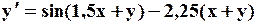


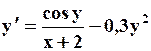

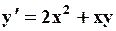
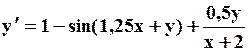
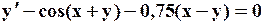
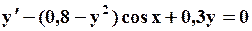


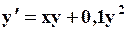



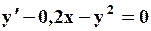
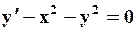
 =
= 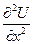 при заданных начальных условиях U(x,0)=f(x) и граничных условиях U(0,t)=
при заданных начальных условиях U(x,0)=f(x) и граничных условиях U(0,t)= 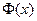 , U(0.6,t)=
, U(0.6,t)= 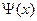 , где tÎ[0,0.01].
, где tÎ[0,0.01].


