
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Однородные дифференциальные уравнения первого порядкаСодержание книги
Поиск на нашем сайте
Определение 1. Однородным дифференциальным уравнением первого порядка называют уравнение, которое можно привести к виду
где функция
Отметим, что функцию Замечание. Однородное дифференциальное уравнение первого порядка путем подстановки Пример 3. Найти общее решение однородного дифферен-циального уравнения первого порядка:
Решение. Введем подстановку
Проинтегрируем обе части
Дифференциальные уравнения второго порядка, допускающие понижение порядка Одним из методов интегрирования дифференциальных уравнений высших порядков является метод понижения порядка. Суть метода состоит в том, что с помощью замены переменной (подстановки) данное дифференциальное уравнение сводится к уравнению, порядок которого ниже. Рассмотрим три типа уравнений, допускающих понижение порядка. Уравнение вида
где Решение уравнения находится понижением порядка и интегрированием. Пример 1. Найти общее решение уравнения
Решение. Путем интегрирования данного уравнения получаем:
Уравнение вида
не содержащее искомую функцию у. Путем подстановки Пример 2. Найти общее решение уравнения
Ведем подстановку Перейдем к уравнению
Это уравнение линейное относительно р. Пусть
перейдем к системе
Решим отдельно (3) и (4). (3):
(4):
Тогда
Возвращаясь к искомой функции у, имеем
Уравнение вида
не содержащее аргумент х. Путем подстановки
приводится к уравнению первого порядка Пример 3. Найти общее решение уравнения
Решение. Уравнение не содержит явный аргумент х, поэтому сделаем подстановку
и данное уравнение примет вид
Это уравнение первого порядка с разделяющимися переменными относительно функции Разделяя переменные, получим
Но Отсюда получим общее решение заданного уравнения:
Линейные однородные уравнения с постоянными коэффициентами Определение 1. Дифференциальное уравнение второго порядка называют линейным однородным уравнением с постоянными коэффициентами, если оно имеет вид
Решение уравнения (1)будем искать в виде
после сокращения на Для нахождения общего решения такого уравнения целесообразно действовать таким образом: 1) составить характеристическое уравнение путем замены
2) решить алгебраическое уравнение, используя формулу:
3) проанализировать возможные корни характеристического уравнения: а) действительные и различные, т.е. б) действительные и равные, т.е. в) комплексные, т.е. 4) в зависимости от значений корней характеристического уравнения общее решение заданного дифференциального уравнения (1) имеет вид: в случае а): в случае б): в случае в): Пример 1. Найти общие решения уравнений: а) б) в) Решение. Для уравнения а) характеристическим уравнением является Найдем корни этого уравнения: Корни характеристического уравнения действительны и различ-ны, поэтому общее решение уравнения а) будет: Для уравнения б) характеристическим уравнением является
Корни характеристического уравнения действительны и равны, поэтому общее решение уравнения б): Для уравнения в) характеристическим уравнением является
Корни этого уравнения комплексные числа, причем
Пример использования дифференциальных уравнений в экономических задачах Пример 1. Экономисты установили, что скорость увеличения инвестированного капитала в любой момент времени
Решение. Пусть Тогда
Необходимо решить задачу Коши для дифференциального уравнения первого порядка. Общим решением дифференциального уравнения является функция
Упражнения к главе 5 1. Найти общее решение или общий интеграл дифферен-циальных уравнений с разделяющимися переменными: 1) 3) 5) 7) 2. Найти общее решение линейных дифференциальных уравнений первого порядка: 1) 3) 5) 7) 3. Найти общее решение однородных дифференциальных уравнений первого порядка: 1) 4) 7) 4. Найти общее решение уравнений Бернулли: 1) 3) 5) 5. Найти решение задачи Коши: 1) 3) 5) 6. Найти общее решение дифференциальных уравнений второго порядка: 1) 3) 5) 7. Найти общее решение уравнений: 1) 3) 5) 8. Решить задачу экономического содержания: Скорость возрастания численности населения пропорциональна численности населения. Найти закон роста численности населения страны, в которой в 2000 году было 50 млн. населения. Сколько населения будет в 2010 году?
5.9 Задания для индивидуальной семестровой работы студентов к главе 5 1. Найти общее решение однородного дифференциального уравнения 1-го порядка 1) 3) 5) 7) 9) 11) 13) 15) 17) 19) 21) 23) 25) 27) 29)
2 Найти общее решение линейного дифференциального уравнения и уравнения Бернулли 1) 3) 5) 7) 9) 11) 13) 15) 17) 19) 21) 23) 25) 27) 29) ЛИТЕРАТУРА 1. Барковський В.В., Барковська Н.В. Вища математика для економістів. – Київ: ЦУЛ, 2002. – 400с. 2. Бугір М.К. Математика для економістів: Посібник. – К.: Видавничий центр “Академія”, 2003. – 520 с. 3. Зимина О.В., Кириллов А.И., Сальникова Т.А. Высшая математика. (Решебник). – 2-е изд., испр. – М.: Физико-математическая литература, 2001. – 368 с. 4. Каплан И.А. Практические занятия по высшей математике. – Харьков: Изд-во Харьк. ун-та, 1968. – 411 с. 5. Красс М.С., Чупрынов Б.П. Основы математики и ее приложения в экономическом образовании: Учеб. – 2-е изд., испр. – М.: Дело, 2001. – 688 с. 6. Красс М.С., Чупрынов Б.П. Математика для экономистов. – СПб.: Питер, 2006. – 464 с.: ил. –(Серия «Учебное пособие»). 7. И.Н. Ляшенко, Е.И. Ляшенко. Математика для экономистов: Учебное пособие для подготовки бакалавров экономического профиля. – 1998. – 228 с. 8. Павленко Т.В., Сукач Т. М. Вивчення інтегрального числення в умовах модульно-рейтингової системи навчання: Навч.посіб. – Алчевськ: ДонДТУ, 2005 – 166 с. 9. Письменный Д.Т. Конспект лекций по высшей математике. 1 часть. — 2-е изд., испр. – М.: Айрис-пресс, 2003. — 288 с. 10. Пискунов Н.С. Дифференциальное исчисление. Т. 1, 2. – М.: Наука, 1985. – 430, 451 с. 11. Ризун В.И. Высшая математика для экономических специальностей, часть II. – Алчевск, ДГМИ, 1999. – 287 с. 12. Ризун В.И. Высшая математика для экономических специальностей. – Алчевск, ДГМИ, 2001. – 214 с. 13. Сукач Т. Н. Линейная алгебра и аналитическая геометрия в примерах и задачах: Учебное пособие для студентов вуза, колледжа. – Алчевск: ДГМИ, 2003 – 121 с.
14. Токунова Т.В. Диференціальне і інтегральне числення: Навч. посіб. – Алчевськ: ДГМІ, 2002. – 175 с.
|
|||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 363; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.92.87 (0.014 с.) |

 ,
, не изменяется при замене х и у на tx и ty, т.е. удовлетворяет условию
не изменяется при замене х и у на tx и ty, т.е. удовлетворяет условию .
. можно привести к уравнению с разделяющимися переменными.
можно привести к уравнению с разделяющимися переменными.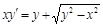 .
.





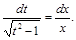



 ,
, – непрерывная на
– непрерывная на  функция.
функция. .
. ;
; .
. ,
, ; и
; и 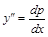 сводится к уравнению первого порядка
сводится к уравнению первого порядка 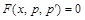 относительно функции
относительно функции  .
. . (1)
. (1)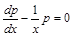 . (2)
. (2) , а
, а  . Подставив в (2)
. Подставив в (2) ;
;  ,
, .
. . Разделим переменные и проинтегрируем:
. Разделим переменные и проинтегрируем:
 .
. ;
;  . Разделим переменные и проинтег-рируем:
. Разделим переменные и проинтег-рируем: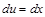 ;
;  .
.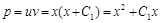 .
. ;
; .
.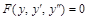 ,
,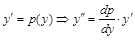 или
или 
 относительно функции р, зависящей от у.
относительно функции р, зависящей от у. .
. , тогда
, тогда 
 или
или  .
. .
. .
.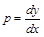 , тогда
, тогда  или
или 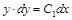 .
. .
. , где
, где  . (1)
. (1) (2). Тогда подставив (2) в (1) вместо
(2). Тогда подставив (2) в (1) вместо  , уравнение (1) обращается в тождество
, уравнение (1) обращается в тождество ;
;  ,
, имеем
имеем 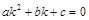 . Функция
. Функция 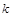 будет корнем квадратного уравнения
будет корнем квадратного уравнения  на
на  ,
,  на
на  . (3)
. (3) ;
; ;
; , где
, где  .
. .
. .
. .
. ;
;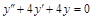 ;
; .
. .
. .
. .
. .
. .
. .
. ,
, 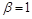 , поэтому общим решением дифференциального уравнения в) является:
, поэтому общим решением дифференциального уравнения в) является: 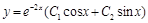 .
.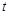 пропорциональна величине капитала с коэффициентом пропорциональности равным согласованному проценту
пропорциональна величине капитала с коэффициентом пропорциональности равным согласованному проценту  инвестиции
инвестиции  .
.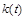 – величина инвестированного капитала в момент времени
– величина инвестированного капитала в момент времени 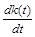 – скорость изменения инвестиции,
– скорость изменения инвестиции, 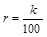 . По условию задачи имеем
. По условию задачи имеем .
. . Учитывая начальное условие
. Учитывая начальное условие  , имеем
, имеем  . Решением задачи Коши является функция
. Решением задачи Коши является функция  .
. ; 2)
; 2)  ;
; ; 4)
; 4)  ;
; ; 6)
; 6)  ;
; .
. ; 2)
; 2) 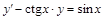 ;
; ; 4)
; 4)  ;
; ; 6)
; 6)  ;
; .
. ; 2)
; 2)  ; 3)
; 3) 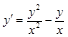 ;
;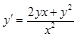 ; 5)
; 5) 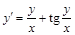 ; 6)
; 6)  ;
; .
. ; 2)
; 2)  ;
; ; 4)
; 4) 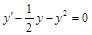 ;
;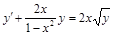 .
. ; 2)
; 2)  ;
; ; 4)
; 4) 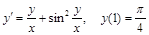 ;
; .
. ; 2)
; 2)  ;
; ; 4)
; 4)  ;
; .
. ; 2)
; 2) 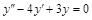 ;
; ; 4)
; 4)  ;
;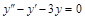 ; 6)
; 6)  .
. . 2)
. 2) 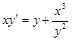 .
. . 4)
. 4) 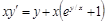 .
. . 6)
. 6)  .
. . 8)
. 8)  .
.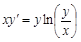 . 10)
. 10)  .
. . 12)
. 12) 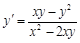 .
. . 14)
. 14)  .
. . 16)
. 16) 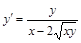 .
. . 18)
. 18)  .
. . 20)
. 20)  .
. . 22)
. 22)  .
. . 24)
. 24)  .
. . 26)
. 26)  .
. . 28)
. 28) 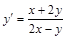 .
. . 30)
. 30)  .
. . 2)
. 2)  .
.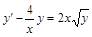 . 4)
. 4) 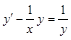 .
.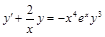 . 6)
. 6)  .
. . 8)
. 8) 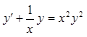 .
.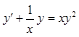 . 10)
. 10)  .
. . 12)
. 12) 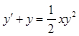 .
.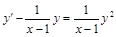 . 14)
. 14)  .
. . 16)
. 16)  .
.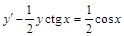 . 18)
. 18)  .
. . 20)
. 20) 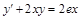 .
. .
. . 24)
. 24)  .
.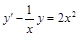 . 26)
. 26)  .
. . 28)
. 28) 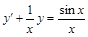 .
. . 30)
. 30) 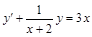 .
.


