
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
К понятию определенного интеграла, как и многих других математических понятий, привели нужды решения задач геометрии, физики и многих практических задач. Рассмотрим несколько таких задач.Содержание книги
Поиск на нашем сайте
Вычисление площади криволинейной трапеции Пусть на отрезке Определение 1. Фигуру, ограниченную кривой В отдельных случаях может Для вычисления площади S этой криволинейной трапеции поделим отрезок
Длины этих частей
Перпендикуляры к оси
Заменим каждую из этих трапеций прямоугольником с основанием Сумма площадей всех таких прямоугольников будет равняться
Таким образом, площадь S криволинейной трапеции приближенно равняется этой сумме, т.е.
Эта формула будет тем точнее, чем меньше величина Чтобы получить точную формулу для вычисления площади S криволинейной трапеции, надо в этой формуле перейти к пределу, когда
Определение определенного интеграла и его содержание Пусть функция
В каждом промежутке
Получим сумму Определение 2. Если существует конечный предел интегральной суммы при
Математически это определение можно записать так:
Числа а и b называются нижним и верхним пределом интегрирования. Функция Согласно этому формулу для вычисления площади S криволинейной трапеции теперь можно записать в виде
Основные свойства определенного интеграла Из определения неопределенного интеграла и основных теорем о пределах вытекают следующие свойства 1. 2. Для любых чисел
3. Постоянный множитель можно выносить за знак определенного интеграла, т.е
4. Определенный интеграл от алгебраической суммы функций равен алгебраической сумме их определенных интегралов:
5. Если функция
6. Если
7. Если функция
8. Если М и т – соответственно, максимум и минимум функции
Формула Ньютона - Лейбница Теорема 1. Непрерывная на отрезке
В формуле (1) переменная интегрирования обозначена буквой t, чтобы избежать путаницы с верхним переменным пределом х. Согласно теореме 1, непрерывная на отрезке
где С – некоторая постоянная. Подставляя сюда
откуда
Полагая
Равенство (3) называется основной формулой интегрального исчисления, или формулой Ньютона - Лейбница. Разность
Формула (4) дает широкие возможности вычисления определенных интегралов. Нужно вычислить неопределенный интеграл и затем найти разность значений первообразной в пределах интегрирования. Пример 1. Вычислить интеграл Решение.
Пример 2. Вычислить интеграл:
Пример 3. Вычислить интеграл:
Методы интегрирования в определенном интеграле Интегрирование по частям Теорема 1. Пусть функции
Разность (1) называется формулой интегрирования по частям в определенном интеграле. Пример 1. Вычислить интеграл Решение. Примем здесь
Пример 2. Вычислить интеграл Решение. Положим
Замена переменной в определенном интеграле Теорема 2. Пусть: 1)
Формула (2) называется формулой замены переменной в определенном интеграле. Пример 3. Вычислить интеграл Решение. Применив формулу замены переменной в определенном интеграле справа налево (здесь роль переменной t сыграет переменная х, получим
Пример 4. Вычислить интеграл Решение. Применим замену переменной Имеем
Несобственные интегралы При изучении определенного интеграла мы выходили из условий конечности отрезка интегрирования и ограниченности на нем подинтегральной функции. Тем не менее, на практике применяются интегралы с бесконечными промежутками интегрирования и интегралы неограниченных функций, с чем связано понятие несобственного интеграла.
Понятие и разновидности несобственных интегралов Согласно теореме существования определенного интеграла этот интеграл существует, если выполненные условия: 1) отрезок интегрирования 2) подинтегральная функция Определение 1. Если хотя бы одно из условий 1) или 2) не выполняется, то определенный интеграл называют несобственным. Если не выполняется первое условие, т.е. Определение 2. Если не выполняется лишь второе условие, то подинтегральная функция
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 387; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.46.212 (0.01 с.) |

 определена непрерывная функция
определена непрерывная функция 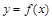 и будем пока что считать, что
и будем пока что считать, что  для всех
для всех  .
. , прямыми
, прямыми  и
и  , называют криволинейной трапецией.
, называют криволинейной трапецией. или
или  и тогда соответствующая сторона трапеции сжимается в точку.
и тогда соответствующая сторона трапеции сжимается в точку. .
. .
.
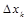 и высотой
и высотой 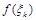 , где
, где 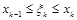 .
. .
. .
. . Тогда
. Тогда .
. задана на отрезке
задана на отрезке 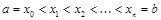 .
. длиной
длиной  выберем произвольную точку
выберем произвольную точку  и вычислим соответствующее значение функции
и вычислим соответствующее значение функции .
. , которую называют интегральной суммой для функции
, которую называют интегральной суммой для функции  , независимый от способа разбиения отрезка
, независимый от способа разбиения отрезка  . (1)
. (1) (2)
(2) – подинтегральным выражением.
– подинтегральным выражением.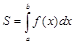 . (3)
. (3)
 .
. имеет место равенство
имеет место равенство .
.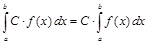 .
.
 , то
, то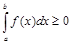 .
.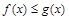 всюду на отрезке
всюду на отрезке  .
. .
. .
. . (1)
. (1) , (2)
, (2) , получаем с учетом свойства 1 определенного интеграла:
, получаем с учетом свойства 1 определенного интеграла: ,
, . Тогда из (2) имеем:
. Тогда из (2) имеем: .
. (3)
(3) условно записывают символом
условно записывают символом  , т.е.
, т.е. (4)
(4) .
. .
. .
. .
.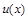 и
и 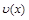 непрерывны вместе со своими производными
непрерывны вместе со своими производными 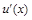 и
и 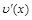 на отрезке
на отрезке  , тогда справедлива формула:
, тогда справедлива формула: . (1)
. (1)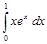 .
. и
и  (тогда
(тогда  ,
, 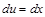 ).
). .
. .
. , тогда
, тогда .
. .
. – дифференцируема на
– дифференцируема на  непрерывна на
непрерывна на 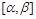 и множеством значений функции
и множеством значений функции  . Тогда справедлива формула
. Тогда справедлива формула . (2)
. (2) .
.
 .
. .
. ,
,  .
.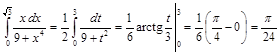 .
. конечен;
конечен; или
или  , или
, или  называют несобственным интегралом от разрывной функции или от функции, неограниченной в точках отрезка интегрирования.
называют несобственным интегралом от разрывной функции или от функции, неограниченной в точках отрезка интегрирования.


