
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Производная сложной и неявной функцииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть Теорема 1. Если
Пример 1. Найти
Решение. Функция
непрерывные в произвольной точке Функции
существуют для любого Таким образом, для функции
Если функция задана неявно уравнением
Если функция
Пример 2. Найти частные производные функции Решение. Имеем:
Итак, по формуле
Пример 3. Найти Решение.
Использование частных производных в геометрии Касательная плоскость и нормаль к поверхности Пусть задана поверхность Уравнение касательной плоскости к заданной поверхности в точке
уравнение нормали –
Порядок нахождения уравнений касательной плоскости и нормали к поверхности: 1. вычисляем частные производные 2. подставляем найденные значения у уравнения (1), (2). Если задано только значение Если поверхность задана уравнением
Пример 1. Найти уравнение касательной плоскости и нормали к поверхности Решение. Запишем уравнение поверхности в виде
Координаты точки М: Вычислим частные производные
Воспользуемся уравнением (1) и (2). Имеем уравнение касательной плоскости
Уравнение нормали
Определение 1. Градиент функции
где Пример 2. Найти градиент функции Решение. Найдем частные производные функции
Вычислим частные производные функции
Вычислим градиент функции
Упражнения к разделу 3.4 Найти частные производные функции: 1.
2. 3.
Найти полный дифференциал функции: 4. 5. 6. Вычислить приближенно: 7. 8. Найти частные производные первого и второго порядка функций: 9.
10.
11.
12.
Найти стационарные точки функций, и исследовать их характер: 13. 14. 15. 16. Найти производные
17.
18.
19.
Найти производные функций 20. 21. Найти градиент функции 22. 23. 24. 25. 26. Найти уравнение касательной плоскости и нормали к поверхности в точке 27.
28.
29.
30.
31.
3.4.8 Задания для индивидуальной семестровой работы студентов к разделу 3.4 1. а) найти б) найти приближенное значение функции в) написать уравнение касательной плоскости и нормали к поверхности 1). 2). 3). 4). 5). 6). 7). 8). 9). 10). 11). 12). 13). 14). 15). 16). 17). 18). 19). 20). 21). 22). 23). 24). 25). 26). 27). 28). 29). 30). 2. Задана дифференцированная функция 1). 2). 3). 4). 5). 6). 7). 8). 9). 10). 11). 12). 13). 14). 15). 16). 17). 18). 19). 20). 21). 22). 23). 24). 25). 26). 27). 28). 29). 30).
3. Исследовать на экстремум функцию 1). 2). 3). 4). 5). 6). 7). 8). 9). 10). 11). 12). 13). 14). 15). 16). 17). 18). 19). 20). 21). 22). 23). 24). 25). 26). 27). 28). 29). 30). Глава 4 ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ Неопределенный интеграл
|
|||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 1785; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.172.243 (0.012 с.) |

 – функция двух переменных
– функция двух переменных  и
и  , каждая из которых является функцией независимой переменной
, каждая из которых является функцией независимой переменной 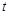 :
:  ,
,  . В этом случае функция
. В этом случае функция  является сложной функцией одной независимой переменной
является сложной функцией одной независимой переменной  функция и
функция и  .
. , если
, если .
. , как функция переменных х, у, дифференцирована во всей плоскости Оху, поскольку имеет частные производные
, как функция переменных х, у, дифференцирована во всей плоскости Оху, поскольку имеет частные производные
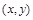 .
.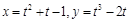 дифференцированы на всей числовой прямой
дифференцированы на всей числовой прямой  , так как производные
, так как производные
 .
. выполняются все условия теоремы. Поэтому для произвольного
выполняются все условия теоремы. Поэтому для произвольного 
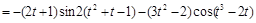 .
. , то производную неявной функции вычисляют по формуле
, то производную неявной функции вычисляют по формуле
 , неразрешенным относительно
, неразрешенным относительно  , то
, то .
. .
. .
.
 , если неявная функция
, если неявная функция 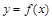 задана уравнением
задана уравнением  .
.

 , точка
, точка  принадлежит этой поверхности и функция
принадлежит этой поверхности и функция  дифференцирована в точке
дифференцирована в точке 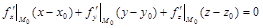 , (1)
, (1) . (2)
. (2)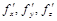 в точке
в точке  ;
; и
и  , то координата
, то координата  точки
точки  определяется из условия, что точка М принадлежит заданной поверхности, т.е.
определяется из условия, что точка М принадлежит заданной поверхности, т.е.  .
. , то уравнение нормали и касательной плоскости имеют вид:
, то уравнение нормали и касательной плоскости имеют вид: ; (3)
; (3) . (4)
. (4) в точке
в точке  .
. , т.е.
, т.е. .
. ,
,  . Координата
. Координата  . Имеем
. Имеем  .
. :
: .
. ;
;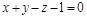 .
. ;
; .
. в точке
в точке  — это вектор, координатами которого являются значения частных производных функции
— это вектор, координатами которого являются значения частных производных функции  ,
, — единичные векторы (орты).
— единичные векторы (орты).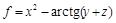 в точке
в точке  .
.


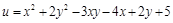 . Найти
. Найти  .
.
 . Найти
. Найти 
 . Найти
. Найти  .
.
 . Найти
. Найти  .
. 
 . Найти
. Найти 
 . Найти
. Найти 
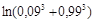 .
. 
 .
. 
 .
.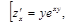




 .
.



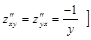
 .
.




 .
.




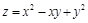 .
.  — стационарная точка и точка минимума,
— стационарная точка и точка минимума, 
 .
.  экстремума нет
экстремума нет 
 .
.  — стационарная точка,
— стационарная точка,  — точка минимума,
— точка минимума, 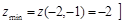
 .
.  — стационарная точка.
— стационарная точка.  — точка минимума,
— точка минимума, 
 ,
,  функции
функции  , где
, где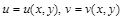 .
. .
.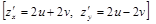
 .
.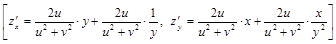
 .
.
 .
. 
 .
. 
 в точке
в точке  .
. 




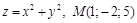 .
.
 .
.
 .
.
 .
.
 .
.
 в точке
в точке  ;
; , если
, если  задано:
задано: ,
, 
 ,
,  .
. ,
, 
 ,
, 
 ,
, 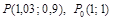
 ,
,  .
. ,
,  .
. ,
,  .
. ,
,  .
. ,
,  .
. ,
,  .
. ,
,  .
.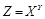 ,
,  .
. ,
,  .
. ,
,  .
. ,
,  .
.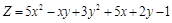 ,
,  .
. ,
,  .
. ,
,  .
. ,
, 
 ,
,  .
. ,
, 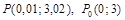 .
. ,
,  .
.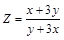 ,
,  .
. ,
,  .
. ,
,  .
. ,
,  .
. ,
,  ,
,  .
.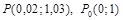 .
. , где
, где  ,
,  . Найти производную
. Найти производную  .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
.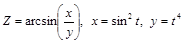 .
. .
. .
. .
. .
. .
. .
. .
. .
. .
.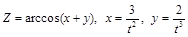 .
. .
. .
.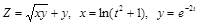 .
. .
. .
. .
. .
. .
. .
. .
. ;
;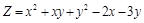 .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
.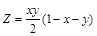 .
. .
. .
. .
. .
. .
.


