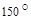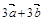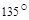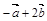Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение рентабельности транспортных поставокСодержание книги
Поиск на нашем сайте
Транспортные затраты перевозки единицы груза у железнодорожным и автомобильным транспортом на расстояние х определяются формулами:
где х измеряется в десятках км. Построим графики транспортных затрат перевозок:
Графики пересекаются в точке
Графики затрат позволяют сделать вывод: а) если б) если Равновесие дохода и затрат Компания изготовляет изделия А и продает их по 2 доллара каждый. Руководство компании определило, что сумма
Определить еженедельное количество изготовления и продажи изделий А, которое обеспечивает равновесие затрат и дохода. Решение. Доход от продажи х тысяч изделий А стоимостью 2 доллара каждый будет:
Для равновесия дохода и затрат необходимо, что бы выполнялось равенство:
Таким образом, эта задача имеет две точки равновесия. Компания может производить 2000 ( Рассмотрим на этом примере возможности компании. Обозначим еженедельный доход Д, тогда:
Из последнего выражения следует, что при Когда Упражнения к разделу 2.2 1. Найти уравнение геометрического места точек, равноудален-ных от точек Ответ: 2 Найти уравнение геометрического места точек, расстояние каждой из которых от прямой Ответ: 3. Найти уравнение окружности, центр которой находится в точке Ответ: 4. Найти уравнение окружности, диаметром которой является отрезок прямой Ответ: 5. Найти центр и радиус окружности Ответ: 6. Найти длины осей, эксцентриситет и координаты фокусов эллипса Ответ: 7. Найти уравнение эллипса, фокусы которого имеют координаты Ответ: 8. Найти уравнение эллипса, у которого длина малой оси равна 6 и один из фокусов имеет координаты Ответ: 9. Найти уравнение эллипса, если известно, что он проходит через точки Ответ: 10. Найти эксцентриситет, координаты фокусов и уравнения асимптот гиперболы Ответ: 11. Найти уравнение гиперболы, у которой фокусы имеют координаты Ответ: 12. Найти уравнение равносторонней гиперболы, проходящей через точку Ответ: 13. Найти координаты вершины и фокуса и уравнения оси директрисы параболы Ответ: 14. Найти уравнение параболы, вершина которой находится точке Ответ: 15. Привести уравнение кривой второго порядка к каноническому виду и построить: 1) 2) 3) 4) Ответ: 1) 2) 3) 4) 16. Найти точки равновесия и области дохода и затрат компании, изготовляющей ежемесячно х изделий стоимостью р гривен, а сумма общих ежемесячных затрат 1) 2) 3) 4) Ответ: 1) 500; 2) 500; 3) 40 или 20; 4) 400.
2.3 Задания для индивидуальной семестровой работы студентов к главе 2 1. Даны три силы
2. Вычислить площадь параллелограмма, построенного на векторах
3. Даны вершины треугольника АВС. Найти: 1) длину стороны ВС; 2) уравнение ВС; 3) уравнение высоты АМ; 4) длину высоты АМ; 5) площадь треугольника АВС; 6) величину угла В;
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 385; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.184.195 (0.009 с.) |

 и
и 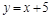 ,
,

 . Для проверки координат точки N найдем точку пересечения аналитически:
. Для проверки координат точки N найдем точку пересечения аналитически: .
.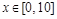 , т.е.
, т.е.  км, транспортные затраты
км, транспортные затраты  перевозок автотранспортом ниже затрат перевозок железнодорожным транспортом;
перевозок автотранспортом ниже затрат перевозок железнодорожным транспортом; , т.е.
, т.е.  км, более рентабельным будет железнодорожный транспорт.
км, более рентабельным будет железнодорожный транспорт. общих еженедельных затрат (в долларах) на изготовление изделия А в количестве х (тысяч единиц) имеет такую закономерность
общих еженедельных затрат (в долларах) на изготовление изделия А в количестве х (тысяч единиц) имеет такую закономерность .
. .
.
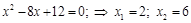 .
. ) изделий А с доходом и затратами 4000 долларов, или 6000 (
) изделий А с доходом и затратами 4000 долларов, или 6000 (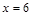 ) изделий с доходом и затратами 10000 долларов.
) изделий с доходом и затратами 10000 долларов.

 , т.е. эти значения х будут точками равновесия.
, т.е. эти значения х будут точками равновесия. , тогда
, тогда  и имеем
и имеем  , т.е. компания получит прибыль. При других значениях х, т.е. когда
, т.е. компания получит прибыль. При других значениях х, т.е. когда  , будем иметь
, будем иметь  – компания понесет убытки.
– компания понесет убытки.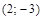 и
и  .
. .
. равно расстоянию от точки
равно расстоянию от точки  .
. .
. и радиус которой равен 4.
и радиус которой равен 4. .
. , содержащийся между осями координат.
, содержащийся между осями координат.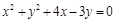 .
.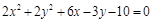 .
. .
. .
. .
. , а длина большой оси равна 10.
, а длина большой оси равна 10. .
. и
и  .
. .
. .
. .
. .
. .
.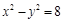 .
. .
. .
. и фокус в точке
и фокус в точке  .
. .
. .
. .
. .
. .
. ; эллипс с центром в точке
; эллипс с центром в точке 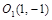 .
. ;
;  ; гипербола, пересекающая ось
; гипербола, пересекающая ось  .
. парабола с осью, параллельной оси
парабола с осью, параллельной оси 
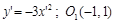 .
. имеет такую закономерность:
имеет такую закономерность: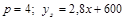 ;
; ;
; ;
; .
.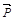 ,
, 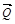 ,
,  , приложенные к одной точке. Вычислить работу равнодействующей силы, когда ее точка приложения перемещается из точки В в точку
, приложенные к одной точке. Вычислить работу равнодействующей силы, когда ее точка приложения перемещается из точки В в точку  .
.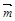 и
и  , если известны:
, если известны: