
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нахождение наибольшего и наименьшего значений функции на отрезкеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Пусть на отрезке 1) найти критические точки функции; 2) вычислить значение функции в критических точках, которые принадлежат отрезку, и на концах отрезка; 3) наибольшее (наименьшее) значение среди образованного множества и будет наибольшим (наименьшим) значением функции, заданной на отрезке Пример 1. Найти наибольшее и наименьшее значение функции Решение. Находим стационарные точки. Для этого найдем производную:
Приравнивая эту производную к нулю и решая уравнение
получаем стационарные точки: Вычисляем значение функции в точках
Итак, наибольшее значение
Интервалы выпуклости и вогнутости кривой, точки перегиба График функции Определение 1. График функции Определение 2. График функции Интервалы выпуклости и вогнутости находят с помощью следующей теоремы: Теорема 1. Если функция Определение 3. Точка, при переходе через которую кривая изменяет выпуклость на вогнутость или наоборот, называется точкой перегиба. Для нахождения точек перегиба графика функции используется следующая теорема: Теорема 2. Если вторая производная Пример 1. Найти интервалы вогнутости, выпуклости и точки перегиба кривой, заданной уравнением Решение. Найдем производные первого и второго порядков:
Приравняем
отсюда находим корни:
таким образом, на интервалах Точки Асимптоты Определение 1. Асимптотой кривой называют прямую, к которой неограниченно приближается точка кривой при неограниченном удалении ее от начала координат. Различают вертикальные, наклонные и горизонтальные асимптоты. Определение 2. Вертикальной асимптотой графика функции Определение 3. Наклонной асимптотой графика функции Если Пример 1. Найти асимптоты графика функции Решение. Функция определена и непрерывна в интервалах 1) 2)
итак,
– наклонная асимптота; 3) Правило Лопиталя Правило Лопиталя-Бернулли является эффективным средством нахождения пределов функции при раскрытии неопределенностей. Раскрытие неопределенностей типа Если функции 1) непрерывны и дифференцируемы в окрестности точки 2) функции 3) существует конечный предел
Раскрытие неопределенностей типа: 1) Неопределенность
2) Неопределенность Так, например, преобразив разность функций 3) Неопределенности типа Пример 1. Вычислить Решение. Если Прологарифмируем:
Если
Тогда Пример 2. Вычислить предел Решение. Проверим выполнение условий теоремы Лопиталя. Пусть
Находим производные:
Выполняются все три условия теоремы Лопиталя. Поэтому
|
||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 1955; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |

 задана непрерывная функция
задана непрерывная функция  , достигающая на данном отрезке своего наибольшего и наименьшего значений. Это может произойти как внутри отрезка, так и на его кон-цах. Отсюда вытекает способ нахождения точек, в которых функция приобретает наибольшее и наименьшее значение на отрезке
, достигающая на данном отрезке своего наибольшего и наименьшего значений. Это может произойти как внутри отрезка, так и на его кон-цах. Отсюда вытекает способ нахождения точек, в которых функция приобретает наибольшее и наименьшее значение на отрезке  на отрезке
на отрезке  .
.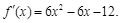
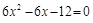 ,
, . Точек, в которых функция не существует, нет.
. Точек, в которых функция не существует, нет. , а также на концах отрезка, т.е. в точках
, а также на концах отрезка, т.е. в точках  :
:
 , наименьшее есть
, наименьшее есть  .
.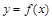 может быть выпуклым или вогнутым.
может быть выпуклым или вогнутым. , если он расположен ниже ее любой касательной на этом интервале.
, если он расположен ниже ее любой касательной на этом интервале. , то график в этом интервале выпуклый. Если
, то график в этом интервале выпуклый. Если 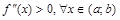 – график вогнутый.
– график вогнутый. при переходе через точку
при переходе через точку  , в которой она равна нулю или не существует, меняет знак, то точка графика с абсциссой
, в которой она равна нулю или не существует, меняет знак, то точка графика с абсциссой  .
. .
. к нулю:
к нулю: ,
, .
. Решая неравенство
Решая неравенство  с помощью метода интервалов, имеем:
с помощью метода интервалов, имеем:  ,
, производная
производная  , кривая вогнута, а на интервале
, кривая вогнута, а на интервале  кривая выпукла.
кривая выпукла. есть точки перегиба кривой.
есть точки перегиба кривой. , когда
, когда  , или
, или  , или
, или  .
. называют прямую
называют прямую  , если функцию можно изобразить в виде
, если функцию можно изобразить в виде  , где
, где  , когда
, когда  (
( ).
). , то
, то  . Тогда
. Тогда  – уравнение горизонтальной асимптоты.
– уравнение горизонтальной асимптоты. .
. и
и  . Ось
. Ось  функция пересекает в точке
функция пересекает в точке  . С осью
. С осью  точек пересечения нет. Найдем асимптоты графика функции:
точек пересечения нет. Найдем асимптоты графика функции: , т.е.
, т.е.  — вертикальная асимптота;
— вертикальная асимптота; ,
,
 ,
,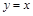
 , таким образом, горизонтальной асимптоты нет.
, таким образом, горизонтальной асимптоты нет. или
или  .
. :
: в этой окрестности;
в этой окрестности; ;
; , тогда:
, тогда: .
. .
. когда
когда 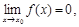
 сводится к неопределенности
сводится к неопределенности 
 когда
когда  , имеем неопределенность
, имеем неопределенность  сводятся к виду
сводятся к виду 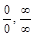 с помощью логарифмирования функции вида
с помощью логарифмирования функции вида  или представляя функцию
или представляя функцию  .
. .
. , то имеем неопределенность
, то имеем неопределенность  .
. .
. , а
, а 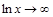 . Тогда:
. Тогда:

 .
.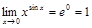 .
.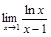 .
. . Будем рассматривать полуинтервал
. Будем рассматривать полуинтервал  , где b > 1 — произвольное число. Тогда
, где b > 1 — произвольное число. Тогда .
. для любого
для любого  , поэтому
, поэтому



