
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Функция, её простейшие свойстваСодержание книги
Поиск на нашем сайте
1. Кривая пересекается прямой х = а в двух точках. Может ли она являться графиком некоторой функции? 2. Может ли график функции быть симметричным: а) относительно оси абсцисс; б) относительно оси ординат? 3. Является ли графиком какой-либо функции множество точек координатной плоскости, изображённое на рис.2.
а) б)
в) г) рис.2
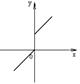
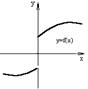
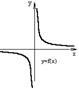
4. Какие из функций, графики которых изображены на рис.3: а) имеют обратную; б) являются монотонными; в) являются возрастающими; г) являются убывающими?
а) б)
в) г)
д) е)
ж) з) рис.3
5. Можно ли утверждать, что функция y =tg x возрастает в своей области определения? 6. Укажите, какие из следующих утверждений верны: а) сумма возрастающих функций есть функция возрастающая; б) разность возрастающих функций есть функция возрастающая; в) произведение двух возрастающих функций есть функция возрастающая; г) всякая монотонная функция имеет обратную; д) всякая убывающая функция имеет обратную; е) если функция имеет обратную, то она или возрастает, или убывает; ж) функция y = tg x имеет обратную; з) функция y = loga x имеет обратную; и) если функция возрастает, то и обратная к ней функция возрастает? 7. Функция возрастает на каждом из промежутков: а) [ –1; 0) и [0; 1]; б) [ –1; 0] и [0; 1]. Обязательно ли она возрастает на отрезке [ –1; 1]? 8. Пусть y = f (x) — возрастающая функция и б) 9. Какие из функций, графики, которых изображены на рис.3, являются чётными, нечетными? 10. Областью определения чётной функции является промежуток [ a; b ]. Что можно сказать о числах а и b? 11. Известно, что функция y = f (x) нечётная и точка х =0 принадлежит её области определения. Чему равно значение функции в этой точке? 12. Существует ли нечётная функция, принимающая только положительные значения? 13. Существуют ли функции, являющиеся одновременно и чётными и нечётными? 14. Верно ли утверждение: а) сумма и разность чётных функций есть функция чётная; б) произведение и частное чётных функций есть функция чётная; в) сумма нечётных функций есть функция нечётная; г) произведение нечётных функций есть функция нечётная; д) сумма чётной и нечётной функций есть чётная? 15. Можно ли подобрать коэффициенты а, b, c, d так, чтобы функция f (x) = a x 3 + b x 2 + c x + d была:
а) чётной; б) нечётной; в) и чётной и нечётной; г) возрастающей; д) убывающей? 16. Может ли возрастающая функция быть: а) чётной; б) нечётной; в) периодической? 17. Может ли чётная функция иметь обратную? 18. Функция y = f (x) имеет наименьший положительный период Т. Какой наименьший положительный период имеет функция: а) y = f (x + a); б) y = f (w x), 19. Имеет ли функции наименьший положительный период, если имеет, чему он равен: а) 20. Может ли сумма периодических функций быть функцией непериодической?
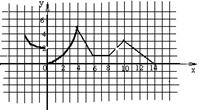
Предел и непрерывность функции в точке 1. На рис.4 изображён график функции y = f (x),
рис.4
а) имеет ли эта функция точки разрыва? б) чему равны значения функции в тех точках разрыва, где она определена? в) имеет ли функция предел в каждой из точек разрыва? г) какие условия непрерывности нарушены в точке разрыва? 2. Пусть х 0 — точка разрыва функции y = f (x). Следует ли отсюда, что: а) точка х 0 не входит в область определения y = f (x); б) не существует 3. Существует ли функция, которая в точке х 0: а) имеет предел, но не определена; б) определена, но не имеет предел; в) определена, имеет предел, но разрывна? 4. Функция y = f (x) непрерывна в точке х 0. Можно ли утверждать, что в этой точке непрерывна функция: а) y = f 2(x); б) 5. Сколько разрывов имеет функция: а) 6. При каком значении а функция будет всюду непрерывной? 7. Функция y = f (x) непрерывна на отрезке [ a; b ] и f (a) f (b)<0. Следует ли отсюда, что уравнение f (x)=0: а) имеет корень на [ a; b ]; б) имеет единственный корень на [ a; b ]? 8. Функция не обращается в нуль в своей области определения. Следует ли отсюда, что функция имеет один и тот же знак при всех х из области определения? Примерный вариант контрольной работы
Вариант 1 №1. Найти пределы: 1) 3) №2. Для данной функции найти а) точки разрыва; б) скачок функции в каждой точке разрыва; в) сделать чертёж.
Вариант 2. №1. Найти пределы: 1) №2. Для данной функции найти: а) точки разрыва; б) найти скачок функции в каждой точке разрыва; в) сделать чертеж.
Литература
Содержание Предисловие…………………………………………………….3 Занятие 1 Основные элементарные функции…………………………………….4 Занятие 2 Числовая последовательность. Предел последовательности……………..9 Занятие 3 Предел функции. Раскрытие неопределённостей вида Занятие 4 Замечательные пределы………………………………….….………31 Решение ИДЗ «Вычисление пределов»…………………………………………….35 Занятие 5 Вычисление пределов при использовании эквивалентностей…………..40 Занятие 6 Обзорное занятие…………………………………………….…….46 Занятие 7 Непрерывность функции……………………………………………49 Контрольные вопросы ………………………………….…….56 Примерный вариант контрольной работы ………………..64 Литература ……………………………………………….…….65
|
||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 558; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.125.91 (0.009 с.) |










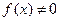 . Будет ли возрастающей функция: а)
. Будет ли возрастающей функция: а)  , k >0;
, k >0; ?
? ; в) y = k f (x),
; в) y = k f (x), 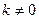 ; г) y = f (x)+ a?
; г) y = f (x)+ a? ; б) у = 2; в) y = cos x; г)
; б) у = 2; в) y = cos x; г) 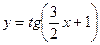 .
.
 ?
? ; в)
; в)  ; г) y = k f (x)?
; г) y = k f (x)? ; б)
; б)  ; в)
; в)  г)
г) 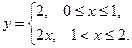

 ; 2)
; 2)  ;
; ; 4)
; 4)  .
.
 ; 2)
; 2)  ; 3)
; 3) 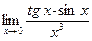 ; 4)
; 4)  .
.
 ,
,  ………..18
………..18


