
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Операции над пределами последовательностей
1. Предел суммы (разности) двух сходящихся последовательностей равен сумме (разности) их пределов:
2. Предел произведения двух сходящихся последовательностей равен произведению их пределов:
В частности: · постоянный множитель можно выносить за знак предела:
· предел натуральной степени от сходящейся последовательности равен этой степени от её предела:
· предел корня k -й степени от сходящейся последовательности равен корню этой же степени от предела последовательности:
№4. Написать первые четыре члена последовательности { xn }, если: 1) ► 1) Подставляя последовательно n =1, 2, 3, 4, … в формулу для общего члена последовательности, найдем: х 1= –1; 2) В соответствии с формулой xn=xn – 1+2 получим: х 2= х 1+2=3, х 3= х 2+2=5, х 4= х 3+2=7. ◄
№5. Какие из следующих последовательностей ограничены сверху? снизу? ограничены? 1) 2; 4; 6; 8; … 2) –1; –4; –9; –16; … 3) –2; 4; –8; 16; …. ► 1) Данная последовательность, состоящая из всех чётных положительных чисел, ограничена снизу, но не ограничена сверху; 2) xn = – n 2<0 (n =1, 2, 3, …), последовательность ограничена сверху, но не ограничена снизу; 3) xn =(–2) n не ограничена, так как для любого числа M >0 можно найти такой номер n, что |xn|=2 n > M. ◄
№6. Какие из последовательностей монотонные, а какие — строго монотонные: 1) xn =2 n +1; 2) –1; –1; –2; –2; –3; –3; … ► 1) данная последовательность строго возрастает, т.к. xn +1=2(n +1)+1=2 n +3>2 n +1= xn для всех натуральных чисел n; 2) данная последовательность невозрастающая, так как
№7. Доказать, что ► Запишем последовательность значений: –1, – отсюда видно, что с возрастанием n значения переменной xn приближаются к нулю так, что с некоторого номера N абсолютные значения переменной будут меньше любого наперёд заданного сколь угодно малого положительного числа Если ε=
Постановка задачи. Пользуясь определением последовательности, доказать, что План решения. 1. Число а называется пределом последовательности { xn }, если для 2. Найти, при каких n справедливо неравенство 3. Если решение имеет вид
⋙Если решение неравенства
№8. Пользуясь определением предела последовательности, доказать, что ► 1. По определению число а =2 называется пределом числовой последовательности 2. Найдём, при каких n справедливо неравенство 3. Неравенство имеет решение
Аудиторные задания №9. Написать первые пять членов последовательности { xn }, если №10. Зная несколько первых членов последовательности { xn }, написать формулу её общего члена: 1, №11. №12. xn = –ln n; Ответ: ограничена сверху. Какие из последовательностей монотонные, а какие — строго монотонные: №13. №14. №15. Используя определение, доказать, что последовательность бесконечно малая №16. Используя определение предела, доказать, что последовательность Написать первые пять членов последовательности { xn }, если: №17. xn = №18. xn = Зная несколько первых членов последовательности { xn }, написать формулу её общего члена: №19. №20. №21. –1, 2, –3, 4, –5, … Какие из последовательностей { xn } ограничены: №22. xn=n 3+2 n. Ответ: ограничена снизу. №23. Какие из последовательностей монотонные, а какие — строго монотонные: №24. Ответ: строго возрастающая, ограниченная. №25. Ответ: строго убывающая, ограниченная сверху.
№26. Пусть { xn }={ n }, Найти последовательности { xn + yn }, { xn – yn }, №27. Доказать, что данная последовательность бесконечно малая: xn = №28. Доказать, что данная последовательность бесконечно большая: xn=n 2. №29. Пользуясь определением последовательности доказать, что
Домашние задания Найти первые четыре члена последовательности { xn }, если: №30. №31. xn= 1. №32. №33. x 1=2, xn =| xn – 1 – 2|. №34. xn = n!, где Зная несколько первых членов последовательности { xn }, написать формулу его общего члена: №35. 2, 5, 10, 17, 26, … №36. –1, 1, –1, 1, –1, … №37. №38. Какие из последовательностей { xn } ограничены, если: №39. xn =sin x. Ответ: ограниченная. №40. №41. №42. Найти последовательности №43. xn=n, yn =1; №44. xn=n 2, yn=n. Доказать, что данная последовательность бесконечно малая: №45. xn = №46. xn= Доказать, что данная последовательность бесконечно большая: №47. xn = №48. xn =2 n. Пользуясь определением последовательности доказать: №49. №50. Занятие 3 Предел функции. Раскрытие неопределённостей вида Цели Знать: v Определение предела; v признаки существования пределов; v основные теоремы о пределах. Уметь: v Применять основные теоремы о пределах; v применять признаки существования пределов при вычислении предела функции; v вычислять пределы, раскрывая неопределённости вида
Определение («на языке последовательностей», или по Гейне) Число А называется пределом функции y=f (x)в точке х 0 (или при
Определение (на «языке ε-δ», или по Коши») Число А называется пределом функции y=f (x)в точке х 0 (или при Основные теоремы о пределах Теорема 1. Предел суммы (разности) двух функций равен сумме (разности) их пределов:
Следствие. Функция может иметь только один предел при Теорема 2. Предел произведения двух функций равен произведению их пределов:
Теоремы 1 и 2 справедливы для любого конечного числа функций. Следствие. Постоянный множитель можно выносить за знак предела:
Следствие. Предел степени с натуральным показателем равен той же степени предела:
Следствие. Теорема. Предел дроби равен пределу числителя, делённому на предел знаменателя, если предел знаменателя не равен нулю:
При нахождении пределов применяют соотношения:
(28).
Постановка задачи. Найти План решения. Для того чтобы найти
№9. Найти пределы: 1) 3) ► 1) Применяя теоремы о пределах, получаем:
= 2) Пределы числителя и знаменателя существуют и предел знаменателя не равен нулю. Пользуясь теоремой о пределе частного, находим: 3) Непосредственно применять теорему о пределе частного нельзя, так как предел знаменателя равен нулю (в знаменателе есть бесконечно малая величина при
Постановка задачи. Найти План решения. Для того чтобы найти Неопределённость вида
· Чтобы раскрыть неопределённость Неопределённость вида
Частный случай: предел рационального выражения вида
№10. Найти пределы: 1) 2) ► 1)
сократим множитель (х – 3) имеем:
2)
В числителе последнего выражения получилась формула — разность квадратов, таким образом:
3)
тогда исходное пределное выражение имеетвид:
которое раскрывается по известным правилам, т.е.:
№11. Найти пределы: 1) 3) ► 1)
2)
3)
4)
№12. Найти пределы: 1) 2) ► Данные предельные соотношения можно рссмотреть, как частное двух многочленов, т.е: 1) 2) 3)
Постановка задачи. Найти План решения. Для того чтобы найти
№13. Найти пределы: 1) ► 1)
2) Рассмотрим два случая: а)
= б)
Аудиторные задания Найти пределы: №51 №52 №53. №54. №55. №56. №57. №58. №59. №60. №61. №62. №63. №64. №65. №66. №67. №68. №69.
Домашние задания Найти пределы: №70. №71. №72. №73. №74. №75. №76. №77. №78. №79. №80. №81. №82. №83. №84. №85. №86. №87. №88. №89. №90. №91. №92. №93.
Дополнительные задания Найти пределы: №94. №95. №96. №97. №98. №99. №100. №101. №102. №103. №104. №105. №106. №107. №108. №109. №110. №11 №112. №113. №114. №115. №116. №117. №118. №119. №120. №121. №122.
Занятие 4 Замечательные пределы Цели Знать: v Замечательные пределы и их следствия. Уметь: v Вычислять пределы, используя замечательные пределы.
Первый замечательный предел
Следствия
Второй замечательный предел
где е Следствия
Постановка задачи. Найти План решения. Для того чтобы найти данный предел следует вычислить 1) если существуют конечные пределы 2) если
3) если
№14. Найти пределы:1) 3) 6) ► 1)
2)
т.к. пределы существуют и они конечны, то 3)
тогда для нахождения исходного предельного выражения воспользуемся формулой:
т.е. имеем 4)
т.е. имеем неопределенность
5)
Тогда,
|
|||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 1784; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.9.115 (0.246 с.) |
 ,
, 

 (17).
(17). (18).
(18).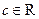
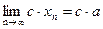 (19);
(19);
 , k =1, 2, 3, … (20);
, k =1, 2, 3, … (20);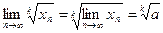 (21).
(21). ; 2) х 1=1, xn = xn – 1+2.
; 2) х 1=1, xn = xn – 1+2. ;
;  ;
; 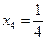 ;
; , n =1, 2, … и некоторые (например, первый и второй) члены этой последовательности равны между собой. ◄
, n =1, 2, … и некоторые (например, первый и второй) члены этой последовательности равны между собой. ◄ есть бесконечно малая.
есть бесконечно малая. , –
, –  , –
, –  , …,
, …,  , …
, … . Докажем это. Пусть дано
. Докажем это. Пусть дано 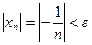 или
или  <
<  , следовательно, можно принять номер N >
, следовательно, можно принять номер N >  N будет выполняться неравенство
N будет выполняться неравенство  . Пусть, например, ε=0,01, тогда
. Пусть, например, ε=0,01, тогда 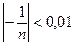 для всех n
для всех n  .
. , то
, то  , т.е. можно принять номер N =3. Следовательно, значения переменной по абсолютной величине
, т.е. можно принять номер N =3. Следовательно, значения переменной по абсолютной величине 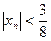 для всех номеров
для всех номеров  . Это и означает, что переменная xn есть бесконечно малая величина. ◄
. Это и означает, что переменная xn есть бесконечно малая величина. ◄ ,
, 
 . Это означает, что
. Это означает, что  имеет решение для
имеет решение для  .
. .
. , если
, если 
 .
. . Следовательно, 2 — предел числовой последовательности
. Следовательно, 2 — предел числовой последовательности  .
. ,
,  , … Определить какие из последовательностей { xn } ограничены:
, … Определить какие из последовательностей { xn } ограничены: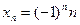 . Ответ: неограниченная.
. Ответ: неограниченная. . Ответ: убывающая.
. Ответ: убывающая. . Ответ: неубывающая.
. Ответ: неубывающая. .
.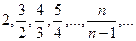 сходится к числу 1.
сходится к числу 1. .
. .
.

 . Ответ: ограниченная.
. Ответ: ограниченная. .
. .
. — две последовательности.
— две последовательности. ,
,  .
. .
.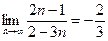 .
. .
. .
. .
.

 . Ответ: ограниченная сверху.
. Ответ: ограниченная сверху.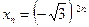 . Ответ: ограниченная снизу.
. Ответ: ограниченная снизу. . Ответ: неограниченная.
. Ответ: неограниченная. и
и  , если:
, если: .
. .
. .
.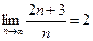 .
. .
. ,
, 
 ,
,  .
. ), если для любой последовательности допустимых значений аргумента xn,
), если для любой последовательности допустимых значений аргумента xn,  , сходящейся к х 0 (т.е.
, сходящейся к х 0 (т.е.  ), последовательность соответствующих значений функции f (xn),
), последовательность соответствующих значений функции f (xn),  ).
). ), если для любого положительно ε найдётся такое положительное число δ, что при всех
), если для любого положительно ε найдётся такое положительное число δ, что при всех 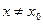 , удовлетворяющих неравенству
, удовлетворяющих неравенству  , выполняется неравенство
, выполняется неравенство  .
. (22).
(22). (23).
(23). (24).
(24).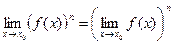 (25).
(25).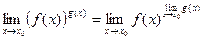 (26).
(26). , (
, ( ) (27).
) (27). , (k =const);
, (k =const);  ;
; ;
;  ;
; ;
; 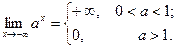
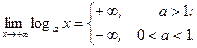 ;
; 
 .
. ; 2)
; 2)  ;
; .
. =
=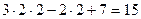 ;
; ;
; ). В числителе имеем ограниченную величину, отличную от нуля. Таким образом, под знаком предела будет произведение ограниченной величины
). В числителе имеем ограниченную величину, отличную от нуля. Таким образом, под знаком предела будет произведение ограниченной величины  , отличной от нуля, на бесконечно большую величину
, отличной от нуля, на бесконечно большую величину 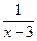 при
при  . ◄
. ◄ или
или  .
. и сокращаем на него, т.к.
и сокращаем на него, т.к.  .
. при
при  будем рассматривать как предел частного двух многочленов, который равен:
будем рассматривать как предел частного двух многочленов, который равен:
 ;
; ; 3)
; 3)  .
. , для раскрытия данной неопределенности средствами алгебры разложим числитель и знаменатель на множители:
, для раскрытия данной неопределенности средствами алгебры разложим числитель и знаменатель на множители: ,
, =
=  ;
; . Данное предельное выражение содержит иррациональность в числителе, следовательно, домножим дробь на сопряженное выражение, т.е. на
. Данное предельное выражение содержит иррациональность в числителе, следовательно, домножим дробь на сопряженное выражение, т.е. на 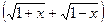 , тогда:
, тогда: .
. ;
;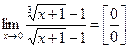 , для раскрытия данной неопределенности сделаем замену:
, для раскрытия данной неопределенности сделаем замену: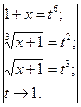
 ,
,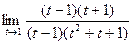 =
=  . ◄
. ◄ ; 2)
; 2)  ;
; ; 4)
; 4)  .
. , для раскрытия данной неопределенности разделим почленно числитель и знаменатель на х 2, тогда:
, для раскрытия данной неопределенности разделим почленно числитель и знаменатель на х 2, тогда: =
=  ;
; , для раскрытия данной неопределенности разделим почленно числитель и знаменатель на х 3, тогда:
, для раскрытия данной неопределенности разделим почленно числитель и знаменатель на х 3, тогда: ;
; , для раскрытия данной неопределенности разделим почленно числитель и знаменатель на n 4, тогда:
, для раскрытия данной неопределенности разделим почленно числитель и знаменатель на n 4, тогда: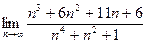 =
=  =
=  ;
; =
= 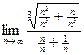 =
=  =0. ◄
=0. ◄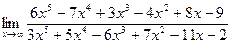 ;
; ; 3)
; 3)  .
. =
=  =2;
=2; ;
; .◄
.◄ ,
,  или др., то данные неопределённости раскрываются путём преобразования и сведения их к неопределённости
или др., то данные неопределённости раскрываются путём преобразования и сведения их к неопределённости  ; 2)
; 2)  .
.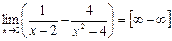 , данное предельное выражение преобразум таким образом:
, данное предельное выражение преобразум таким образом: =
=  ;
; . Перенеся иррациональность из числителя в знаменатель, получим:
. Перенеся иррациональность из числителя в знаменатель, получим: =
=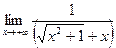 =0;
=0; . ◄
. ◄ . Ответ: 5.
. Ответ: 5. . Ответ:
. Ответ:  .
. . Ответ: 0.
. Ответ: 0. . Ответ:
. Ответ:  .
. . Ответ: 2.
. Ответ: 2. . Ответ: –
. Ответ: –  .
. . Ответ:
. Ответ:  .
.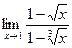 . Указание: замена: x = t 6. Ответ:
. Указание: замена: x = t 6. Ответ:  .
. . Ответ: 0.
. Ответ: 0. . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  .
. . Ответ: –9.
. Ответ: –9. . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  . Ответ:
. Ответ:  .
. . Ответ: 4.
. Ответ: 4. . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  .
.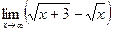 . Ответ: 0.
. Ответ: 0. . Ответ: 40.
. Ответ: 40. . Ответ:
. Ответ:  .
. . Ответ: 4.
. Ответ: 4. . Ответ: 0.
. Ответ: 0. . Ответ:
. Ответ:  . Ответ:
. Ответ:  . Ответ:
. Ответ:  . Ответ: 1.
. Ответ: 1. . Ответ:
. Ответ:  .
.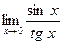 . Ответ:1.
. Ответ:1. . Ответ:
. Ответ:  . Ответ:
. Ответ:  . Ответ:
. Ответ:  . Ответ:
. Ответ: 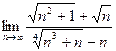 . Ответ: –1.
. Ответ: –1. . Указание: замена х +11= t 4. Ответ:
. Указание: замена х +11= t 4. Ответ:  .
. . Ответ:
. Ответ:  . Ответ:
. Ответ: 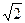 .
. . Ответ:
. Ответ:  . Ответ: 1.
. Ответ: 1.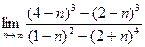 . Ответ: 0.
. Ответ: 0. . Ответ: 0.
. Ответ: 0. . Ответ:
. Ответ: 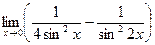 . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  . Ответ: 2.
. Ответ: 2. . Ответ:
. Ответ:  .
. . Ответ: –1.
. Ответ: –1. . Ответ: 2.
. Ответ: 2. . Ответ:
. Ответ:  . Ответ: 1.
. Ответ: 1. . Ответ: 0.
. Ответ: 0. . Ответ:
. Ответ: 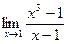 . Ответ: 3.
. Ответ: 3. . Ответ:
. Ответ:  .
.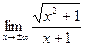 . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  . Ответ:
. Ответ: 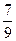 .
. . Ответ:
. Ответ: 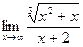 . Ответ: 0.
. Ответ: 0. . Ответ:
. Ответ:  . Ответ: 5.
. Ответ: 5. . Ответ:
. Ответ:  . Ответ: 1.
. Ответ: 1. . Ответ: 1.
. Ответ: 1. . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  .
. . Ответ: 1.
. Ответ: 1. (29).
(29). ,
, ,
,  ,
, ,
,  ,
, ,
,  .
. ,
,  , (30)
, (30)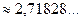 — число Эйлера.
— число Эйлера. ;
; ,
,  ;
;  ;
; ;
;  , (а =const).
, (а =const). .
. и
и  ;
; ;
;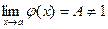 и
и  , то С находится с помощью формул:
, то С находится с помощью формул: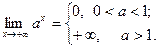

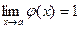 и
и  , где
, где  при
при  , получим:
, получим: =
=  .
. ; 2)
; 2)  ;
; ; 4)
; 4)  ; 5)
; 5)  ;
; ; 7)
; 7)  .
. . Воспользуемся первым замечательным пределом:
. Воспользуемся первым замечательным пределом: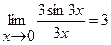 ;
; . Вычислим пределы двух функций:
. Вычислим пределы двух функций: ,
, . Вычислим пределы двух функций:
. Вычислим пределы двух функций: ,
, , следовательно
, следовательно  . Вычислим пределы двух функций:
. Вычислим пределы двух функций:
 . Для раскрытия данной неопределенности воспользуемся вторым замечательным пределом, т.е.:
. Для раскрытия данной неопределенности воспользуемся вторым замечательным пределом, т.е.: =
=  ;
; . Введем замену:
. Введем замену:
 =
=


