Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вычисление пределов при использовании эквивалентностейСодержание книги
Поиск на нашем сайте
Цели Знать: v Эквивалентные бесконечно малые функции и основные теоремы о них. Уметь: v Вычислять пределы, используя основные теоремы эквивалентности.
▼ Если Важнейшие эквивалентности (31) 1. sin x~x при 2. tg x~x при 3. arcsin x~x при 4. arctg x~x при 5. 1 – cos x~ 6. e x – 1 ~x при 7. a x – 1 ~x ln a при 8. ln(1+ x) ~x при 9. 10. (1+ x) k – 1 ~k x, k> 0 при в частности, Постановка задачи: Вычислить предел План решения: Бесконечно малые функции, стоящие в числителе и знаменателе, следует заменить на им эквивалентные, используя основные эквивалентности (31). Если f (x), f 1(x), g (x), g 1(x) — бесконечно малые функции в точке х =0, такие, что f (x)~ f 1(x) и g (x)~ g 1(x) в точке х =0, и существует
Постановка задачи: Вычислить предел План решения: 1.Нужно заменить f (x) и g (x) на эквивалентные им бесконечно малые функции. Но важнейшие эквивалентности существуют при х =0. Поэтому сначала сделаем замену переменной х – а = t и будем искать предел при 2. Преобразуем выражение под знаком предела, пользуясь алгебраическими и тригонометрическими формулами, и заменяя в произведении и частном бесконечно малые функции эквивалентными.
Постановка задачи: Вычислить предел План решения: 1. Преобразуем выражение под знаком предела: 2. Поскольку показательная функция е х непрерывна, то можно перейти к пределу под знаком функции. Имеем:
3. Вычисляем предел показателя Постановка задачи: Вычислить предел План решения: Чтобы использовать таблицу эквивалентных бесконечно малых, сделаем замену переменной t = x – a (тогда 2. Поскольку показательная функция ех непрерывна, то можно перейти к пределу под знаком этой функции. Имеем 3. При вычислении предела
№15. Найти пределы: 1) 3) ► 1) = 2) = = 3) = = 4) =
=
Аудиторные задания Найти пределы: №161. №162. №163. №164. №165. №166. №167. №168.
Домашние задания Найти пределы: №169. №170. №171. №172. №173. №174. №177. №178. №179.
Дополнительные задания Найти пределы: №180. №181. №182. №183. №184. №185. №186. №187. №188. Занятие 6 Обзорное занятие Цель: обобщить знания, полученные на предыдущих занятиях, отрабротать навык нахождения пределов.
При нахождении пределов используют соотношения:
Найти пределы: №189. №190. №191. №192. №193. №194. №195. №196. №197. №198. №199. №200. №201. №202. №203. №204. №205. №206. №207. №208. №209. №210. №211. №212. №213. №214. №215. №216. №217. №218. №219. №220. №221.
Занятие 7 Непрерывность функции Цели Знать: v Определения: непрерывность функций; непрерывность функции в точке, интервале и на отрезке; v основные теоремы о непрерывных функциях и свойства функций, непрерывных на отрезке; v классификацию точек разрыва. Уметь: v Определять точки разрыва функции.
▼ Пусть функция y = f (x) определена в точке х 0 и в некоторой окрестности этой точки. Функция y = f (x) называется непрерывной в точке х 0, если существует предел функции в этой точке и он равен значению функции в этой точке, т.е.
▼ Функция y = f (x) называется непрерывной в точке х 0, если она определена в точке х 0 и её окрестности, и бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции, т.е.
▼ Функция y = f (x) называется непрерывной в точке х 0, если её левосторонний и правосторонний пределы существуют, между собой равны и равны значению функции в этой точке, т.е.
⋙При нахождении предела непрерывной функции f (x) можно перейти к пределу под знаком функции, т.е. в функцию f (x) вместо аргумента х подставить его предельное значение х 0: lim sin x =sin(lim x); lim arctg x =arctg (lim x); (35) lim lg x =lg (lim x).
Постановка задачи: Дана функция y = f (x), пользуясь определением непрерывности функции доказать, что функция непрерывна в произвольной точке х 0 области определения данной функции. План решения: Проверить выполнение условий непрерывности функции y = f (x) в точке х 0:
Если хотя бы одно из условий не выполнено, то функция y = f (x) в точке х 0 имеет разрыв.
№16. Пользуясь определением непрерывности функции доказать, что функция у = х 2 непрерывна в произвольной точке „ Пусть
= Теперь, применяя теоремы о пределе суммы и произведения функций, получим:
= Таким образом,
№17. Доказать, что функция
не является непрерывной в точке х 0=0, но непрерывна справа в этой точке. Построить график функции f (x). ► Найдём односторонние пределы в точке х 0=0. Слева от точки х 0 имеем f (x)=0, поэтому Кроме того, f (x 0) = f (x)=1, откуда следует, что
рис.1
График функции изображен на рис.1. ◄
Постановка задачи: Исследовать на непрерывность функцию y = f (x) в точке х 0. План решения: Найти односторонние пределы функции y = f (x) в точке х 0, т.е.
№18. Исследовать на непрерывность функцию
► Функция у = х, у = sin x и у =1 непрерывны на всей числовой прямой, поэтому данная функция может иметь разрывы только в точках, где меняется её аналитическое выражение, т.е. в точках Исследуем функцию на непрерывность в этих точках, для чего найдём соответствующие односторонние пределы и значения функции. В точке
Таким образом, в точке Скачок функции f (x) в точке Для точки
а значение
№19. Установить характер разрыва функции ► Находим:
Аудиторные задания Пользуясь определением, доказать непрерывность функции f (x) в каждой точке №212. f (x)= x 3. №213. f (x)=4 x 2 – 5 x +2. №.214. Доказать, что функция не является непрерывной в точке х 0=1, но непрерывна слева в этой точке. Построить график функции. №.215. Доказать, что функция не является непрерывной в точке х 0= –2, но непрерывна справа в этой точке. Построить график функции.
Исследовать на непрерывность и построить график функции. Найти скачок функции в точках разрыва: №.216. Ответ: 1) функция терпит разрыв 1-го рода в точке х = –2; скачок функции равен –2; и имеет устранимый разрыв в точке х =2. В остальных точках функция непрерывна. №.217. Ответ: Функция имеет устранимый разрыв в точке х =1 и терпит разрыв 1-го рода в точке х =2; скачок функции равен 4. В остальных точках функция непрерывна.
Установить характер разрыва функции в точке х 0: №218. Ответ: х 0= – 4 — точка устранимого разрыва. №219. Ответ: х 0 = 0 — точка устранимого разрыва.
Домашние задания Пользуясь определением, доказать непрерывность функции f (x) в каждой точке №220. №221. №222. №223. №224. Пользуясь определением непрерывности функции, доказать: №225. Функция №226. Функция №227. Функция f (x) =cos x непрерывна в точке х = 0. Исследовать на непрерывность и построить графики следующих функций: №228. №229. №230. №231. №232. №233. Контрольные вопросы
|
||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 1427; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.93.168 (0.009 с.) |

 , то α и β называются эквивалентными бесконечно малыми (при
, то α и β называются эквивалентными бесконечно малыми (при  ), это обозначается: α ~ β. ▲
), это обозначается: α ~ β. ▲ ;
; при
при  ~
~  при
при  ~
~  .
. , где f (x) и g (x) — бесконечно малые функции в точке х =0.
, где f (x) и g (x) — бесконечно малые функции в точке х =0. , то существует
, то существует  , где f (x) и g (x) — бесконечно малые функции в точке х = а.
, где f (x) и g (x) — бесконечно малые функции в точке х = а. .
. , где
, где  и
и  .
. .
. =
=  .
. , заменяя бесконечно малые функции эквивалентными.
, заменяя бесконечно малые функции эквивалентными. , где
, где  и
и  .
. ) и преобразуем выражение под знаком предела:
) и преобразуем выражение под знаком предела:  .
. .
. заменяем бесконечно малые функции эквивалентными.
заменяем бесконечно малые функции эквивалентными. ; 2)
; 2)  ;
; ; 4)
; 4)  .
. =
=  =
= =4;
=4; =
=  =
= =
=  =
= =
=  ;
; =
=  =
= =
=  =
= =
=  ;
; =
=  =
= =
=  =
= =
=  =
= =
=  . ◄
. ◄ . Ответ:
. Ответ:  .
. . Ответ: 1.
. Ответ: 1. . Ответ: 3.
. Ответ: 3. . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  .
. . Ответ:
. Ответ: 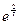 .
. . Ответ:
. Ответ:  .
. . Ответ: ln 5.
. Ответ: ln 5. . Ответ: 1.
. Ответ: 1. . Ответ: –1.
. Ответ: –1. . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  .
. . Ответ: е.
. Ответ: е. . Ответ: 2.
. Ответ: 2. . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  . Ответ:
. Ответ:  .
. . Ответ: е -1.
. Ответ: е -1. . Ответ:
. Ответ:  , (а =const);
, (а =const); ;
;  где
где  ,
,  ;
; ;
;  ;
; ;
; 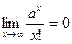 ;
;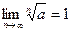 ;
;  .
.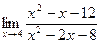 . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  .
. . Ответ: е –2.
. Ответ: е –2.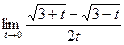 . Ответ:
. Ответ:  .
. . Ответ: 0.
. Ответ: 0. . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  .
. . Ответ: –2.
. Ответ: –2. . Ответ:
. Ответ: 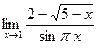 . Ответ:
. Ответ:  .
.
 . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  .
. . Ответ: ¥.
. Ответ: ¥. . Ответ: 2.
. Ответ: 2. . Ответ: 2.
. Ответ: 2. . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  . Ответ: 1.
. Ответ: 1. . Ответ: –1.
. Ответ: –1. . Ответ: 3.
. Ответ: 3. . Ответ: 1.
. Ответ: 1. . Ответ:
. Ответ:  .
. . Ответ: е –2.
. Ответ: е –2. . Ответ: 0.
. Ответ: 0. . Ответ: –2.
. Ответ: –2. . Ответ: е –2.
. Ответ: е –2. . Ответ: – е.
. Ответ: – е. . Ответ:
. Ответ:  .
.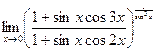 . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  .
. . Ответ: е 3.
. Ответ: е 3. . Ответ:
. Ответ:  .
. (32). ▲
(32). ▲ (33). ▲
(33). ▲ (34). ▲
(34). ▲ ;
; .
. — приращение аргумента в точке х 0. Найдём соответствующее приращение функции:
— приращение аргумента в точке х 0. Найдём соответствующее приращение функции: =
=  =
= =
=  .
. =
=  =
= .
. , что и означает (по определению) непрерывность данной функции в точке
, что и означает (по определению) непрерывность данной функции в точке  . ◄
. ◄
 . Аналогично,
. Аналогично,  .
. . Это означает, что в точке х 0=0 не выполнены все условия непрерывности функции, но функция f (x) непрерывна справа в этой точке.
. Это означает, что в точке х 0=0 не выполнены все условия непрерывности функции, но функция f (x) непрерывна справа в этой точке.
 и
и  , при этом:
, при этом: , то х 0 — точка конечного разрыва;
, то х 0 — точка конечного разрыва;
 и
и  .
. имеем:
имеем: ,
, ,
, .
. функция имеет разрыв 1-го рода и непрерывна слева.
функция имеет разрыв 1-го рода и непрерывна слева. .
. ,
, ,
, не определено. Отсюда следует, что
не определено. Отсюда следует, что  в точке х 0=2.
в точке х 0=2. ,
,  , т.е. функция в точке х 0=2 не имеет ни одного из односторонних пределов. Отсюда следует, что х 0=2 — точка разрыва 2-го рода. ◄
, т.е. функция в точке х 0=2 не имеет ни одного из односторонних пределов. Отсюда следует, что х 0=2 — точка разрыва 2-го рода. ◄



 , х 0= – 4.
, х 0= – 4. , х 0=0.
, х 0=0. .
. .
. .
. .
. .
. непрерывна в точке х = –2.
непрерывна в точке х = –2. непрерывна в точке х = 4.
непрерывна в точке х = 4.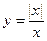 .
.